LWE
在所有后量子密码体制中,格是研究最活跃和最灵活的。它们具有很强的安全性,能够进行密钥交换、数字签名,以及构造出像全同态加密这样复杂的算法。尽管格密码体制的优化和安全性都需要非常复杂的数学证明,但基本思想只需要基本的线性代数。假设你有一个如下线性方程组:
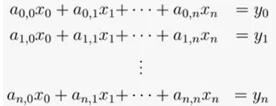
求解x是一个经典的线性代数问题,可以用高斯消元法快速求解。另一种思考方式是我们有一个神秘的函数,
给定向量a,我们在不知道x的情况下,得到了ax的结果,在查询这个函数足够多次之后,我们可以在短时间内学习f(通过求解上面的方程组)。通过这种方式,我们可以将线性代数问题重新定义为机器学习问题。
现在,假设我们在函数中引入了少量噪音,即在x和a相乘之后,我们加上一个误差项e,然后整体模上一个(中等大小的)素数 q,最后我们包含噪音的神秘函数看起来是这样的:
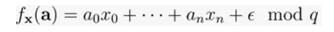

学习这种带噪音的神秘函数已经在数学上被证明是极其困难的。直觉告诉我们,在这种情况下使用高斯消元,它的每一步都会使误差项e变得越来越大,直到它超过关于函数的所有有用信息。在密码学文献中,这被称为错误学习问题(LWE)。
基于LWE的密码学之所以被称为是基于格的密码学,是因为LWE的困难性证明依赖于这样一个事实,即在格中找到最短向量,已知它属于NP-hard问题。在这里,我们不会深入讨论格的数学问题,但我们可以把格看作是n维空间的平铺图:

格是由坐标向量表示的。在上面的例子中,通过结合e1、e2和e3(通过法向量加法)可以到达格中的任何点。最短向量问题(SVP):给定一个格,找到向量长度最短的元素。这很难直观的原因是因为并非所有给定格的坐标系都同样易于使用。在上面的例子中,我们可以用三个非常长且非常接近的坐标向量来表示格,这使得找到接近原点的向量变得更加困难。事实上,有一种规范的方法可以找到格的“最坏可能”表示。当使用这种表示时,已知最短向量问题为NP-hard问题。
在讨论如何使用LWE进行抗量子密码研究之前,我们应该指出的是LWE本身并不是NP-hard问题。它不是直接归约为SVP,而是归约为SVP的近似值,根据推理,它实际上不是NP-hard问题。尽管如此,目前还没有多项式(或次指数)时间内的算法来求解LWE。
现在让我们使用LWE问题来构建一个实际的密码体制。最简单的方案是由Oded Regev在他最初的论文中构造的,同时他也证明了LWE问题的困难度。这里,密钥是一个n维的整系数模q的向量,也就是上面提到的LWE私钥。公钥是前面讨论的矩阵A,以及LWE函数的输出向量。

这个公钥的一个重要特性是,当它乘以向量(-sk,1)时,我们得到误差项,大约为0。
为了加密一位消息m,我们取A的随机列之和,并在结果的最后一个坐标中编码m,即如果m为0,就加0,如果m为1,就加q/2。换句话说,我们选择一个元素为0或1的随机向量x,然后计算:
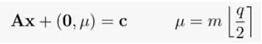
直观地说,我们已经求解了LWE函数(我们知道它很难被破解)的值,并在这个函数的输出中编码了m。
解密是有效的,因为知道了LWE私钥就将允许接收方收回消息,外加一个小的错误项。
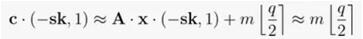
正确选择错误分布后,它将不会使消息失真超过q/4。接收方可以测试输出是否接近于0或q/2 mod q,并相应地解码出m。
该体制的一个主要问题是它需要很大的密钥。要加密一位消息,需要在安全参数中使用大小为n2的公钥。然而,格密码体制的一个吸引人的方面是它们的速度非常快。
自从Regev的第一篇论文发表以来,围绕基于格密码体制的研究进行了大量工作。其中关于改进其实用性的一个关键突破是Ring-LWE,Ring-LWE是LWE问题的一个变体,其中密钥是由若干多项式表示的。这导致了密钥大小的二次减少,加速了加密和解密,仅使用n*log(n)次操作(使用快速傅立叶变换,FFT)。
Kyber是一种密钥封装机制(KEM),它遵循与上述系统类似的构造,但是使用了一些奇特的代数数论来获得比Ring-LWE更好的性能。对于合理的安全参数,密钥大小约为1kb(仍然很大),但加密和解密时间大约为0.075毫秒。考虑到这种速度是通过软件实现的,Kyber KEM似乎很有希望用于后量子密码中的密钥交换。
Dilithium是一种基于与Kyber类似技术的数字签名方案。它的细节超出了本文的范围,但值得一提的是,它也实现了相当不错的性能。公钥大小约为1kb,签名为2kb。这也非常高效。在Skylake处理器上,计算签名所需的平均周期约为200万次。验证的平均周期为39万次。
摘自 http://www.qukuaiwang.com.cn/news/13589.html
图示

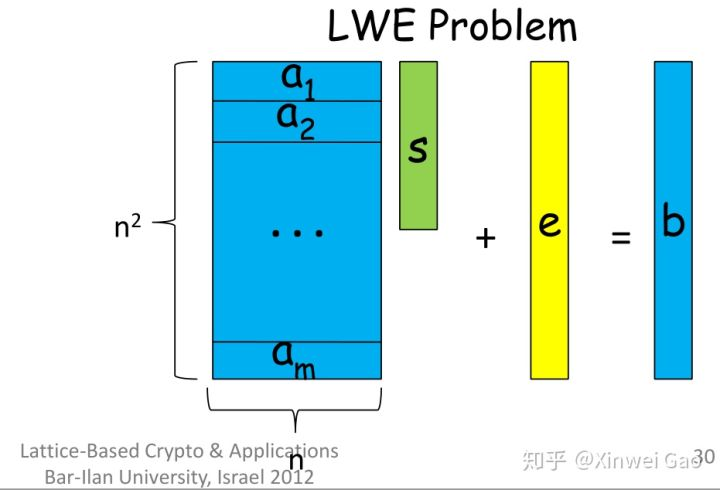
如图在 LWE 问题中,蓝色的部分是均匀随机的(或与均匀随机不可区分), 是私钥,
是不公开的部分。简单来说,就是一个均匀随机的矩阵,乘上服从某个分布的私钥,再加上一个服从某个分布的错误扰动项,计算得到的
与均匀随机不可区分

RLWE 与 LWE 问题很类似,只不过在 RLWE 问题中,和 LWE 相比,直观的看所有元素要"小了很多"。因为 RLWE 中,每个部分都是一个多项式,而不是 LWE 问题中的矩阵。这极大的提高了方案的实际效率,并减小了通信开销。
摘自 https://zhuanlan.zhihu.com/p/45880224
格
格的定义如下:格 是线性空间
上确定的一组线性无关的向量的整数线性组合。格
的基
的每个分量线性无关,
。
为格
的一组基。注意同一个格可以由不同的格基表示。
简单来说,我们常见的二维坐标系可以看做一个格。每个格有很多组格基,格基的线性组合可以得到格中全部的点。对于二维坐标系,向量 和
就是最简单的一组格基。
密码学中用的格当然不是二维的,一般来说,达到足够安全性的方案,格的维度在 1000 左右。
理想格
一般的lattice 通常是定义在 空间上,同构于
. 要想表示这个lattice,我们肯定就需要用这个lattice的一组基:
就是 n 个 n维向量,那这个表示所占用的空间就是 规模。
lattice-crypto 经常用的case,就是 SIS lattice,即 SIS 问题的所有整数解。

很明显,要描述这个lattice,要靠矩阵A,那就意味着需要存 比特数据。数据量实在是不小。
因此,[LPR10] 就是想,我们能不能用一个更小的量来描述一个lattice呢。
所以,才会使用数域(number field)这个数学结构。
在任何一本讲代数数论的书上,都会讲,一个扩张次数为 n 的数域,一定存在n个复嵌入,这就把数域中的数映射到 里面去了。
也就是讲,数域 中的任何一个数 x 都可以映射到一个向量
。

上述方程的解集 I 显然就是一个理想嘛。用上数域之后,一个 SIS 风格的lattice就只需要靠 就可以描述。存储量是不是大幅降低,这样才有可能在实际环境部署一个 lattice-crypto的方案嘛。
摘自 https://www.zhihu.com/question/364968828
https://zhuanlan.zhihu.com/p/45880224
https://blog.csdn.net/weixin_43255133/article/details/83031862