这里讨论组合优化中初始解的生成问题。组合优化问题,很多情况下,解的生成是随机的或者是采用某种直观上满足题意的初始化方法,要知道初始解对于找到局部最优乃至是最好的解是极其重要的,就好比条条大路通罗马,或者你直接就出生在罗马。接下来要说明的算法是在进行各种不同的启发式算法求解之前,对初始解进行优化的算法且比较通用。
在实际问题中,目前笔者暂时遇到的可以使用的地方一个是用于解的生成,还有一个地方就是在启发式算法迭代求解的过程中,在解的再生成中应用这种λ-optimal算法的思想。
描述问题或者算法要有头有尾,先说明问题,之后算法的描述建立在此之上,也就更加通俗易懂。
TSP问题介绍
旅行推销员问题可以这样表述:“要求推销员在给定的n个城市中访问一次且仅访问一次,从任意一个城市出发,返回出发地。他应该选择什么样的路线或旅行,以使总旅行距离最小化?”除了距离,还可以考虑时间、成本等其他概念。
在数学中,可以描述为:
在一个无向完全图中,把城市看作坐标点,每个城市之间都有路,且一般路径长度用欧氏距离描述
给定一个"成本矩阵" D = (D i j),dij(i,j是下标)为i城市和j城市之间的距离成本,且dij=dji
P = (i1, i 2 , i2 ,… , in) 是城市的集合
而总的花销为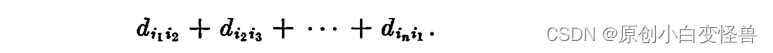
目标函数是Q,公式为
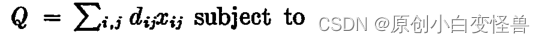
且有如下约束条件
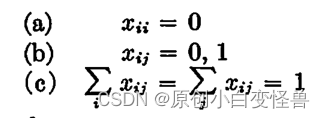
xij=1表示i城市到j城市之间有边(即选择这条路作为解中的一部分)
反之xij=0就是没走过
且要求一个城市一定会被到达且也会从当前城市再出去,以形成回路,且只经过一次
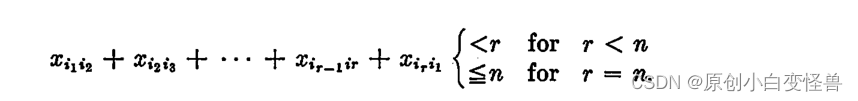
上式代表回路经过的边数为r(城市的个数为r-1)
λ-optimal
λ-optimal算法就是用于初始化更有效的大规模(这里规定n>31)TSP的解时,所提出的方法
定理与定义
定义:如果一个回路是λ-optimal,则其不可能通过将任意λ条链接替换为其他任何一组λ条链接,以更低的成本
获得一个回路。
定理1:T是一个回路,且有k个城市的位置已经是最优解的一部分。则有T是最优的,或者k<n-λ
定理2:任何回路都是1-optimal
定理3:接下来的三句话等价
回路是2-optimal
回路相对于倒置是最优的;这里的倒置指的是将一组相邻城市的顺序颠倒过来。
回路本身不相交(在非欧氏距离矩阵的广义意义上)。
定理4:回路的代价是最小的,当且仅当其是n-optimal
定理5:设Cλ是包含所有λ-optimal回路的集合,则有包含关系C1属于C2属于C3...属于Cn
定理6:当回路能通过插入和反转操作达到最优时,它是3-optimal的。
算法描述与伪代码
我们在这里提到了3-opt tour的另一种描述,它更形象生动。
对于长度为k的连续城市序列,比如(t1,t2,…tk)(k < n,n为城市的总数),我们将其作为连续的整体从队列中取出,然后再重新插入或者反转之后重新插入,执行以下操作之后会得到更好的T’(路程的总花费最小)。
对每个随机生成的旅行序列,我们重复以上的操作,直到无法优化,则将它加入下一步启发式算法将要迭代的初始解集合中去。
将它们描述为伪代码如下
初始化初始解集合为空集S
当初试S的规模没达到m时:
随机初始化解
对解中每个连续的3个城市序列
判断是否能从中取出再重新插入可以达到更好的解
加入S
算法的优化
为了使每次被插入之后的序列不再被重新插入,因为可能此序列较优,会一直参与循环,这是有可能发生的,为了尽量减少这样的事发生,做出如下改进:
在每次得到(t1,t2,t3,…tn-1,tn)之后,将其进行循环右移,变成
(tn,t1,t2,t3,…,tn-1)
当然还有一个更复杂的方法,在实现起来也较为困难,且笔者认为初始解的生成上也没有必要花这么大功夫,但是还是说明一下。这里就采用了禁忌搜索的思想:
我们将之前通过原始算法产生的k1个解记录成集合S’,在计算第k1+1个解时,当插入了序列k到了某个位置中去,且这种操作在S‘中有发生的花=话,我们就不这样更新;只有当没有其他更好的更新发生时,我们才做这样的更新。这样能扩大解的空间和初始化解的效率。
参考文献
Computer Solutions of the Traveling Salesman Problem. By SHEN LIN (Manuscript received August 18, 1965)