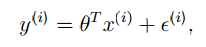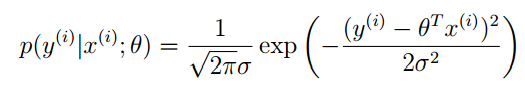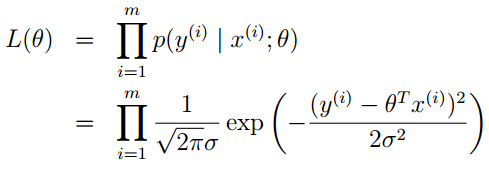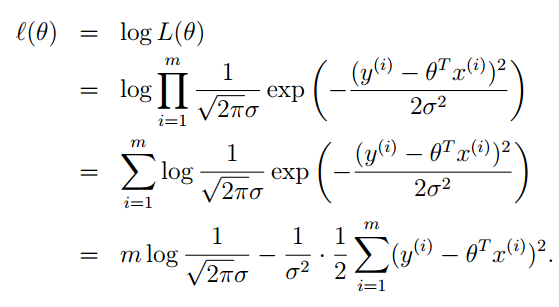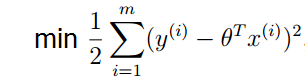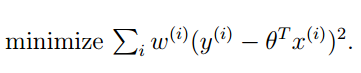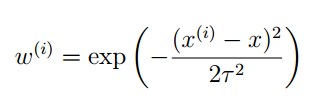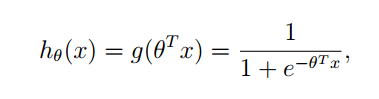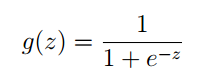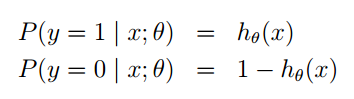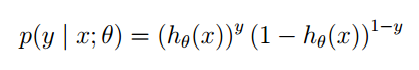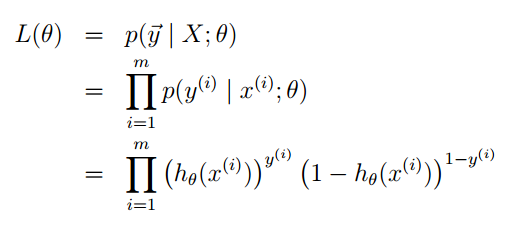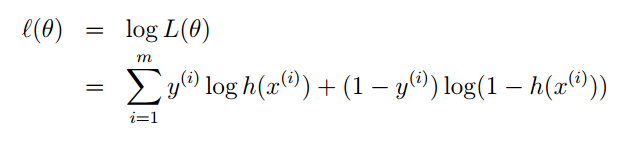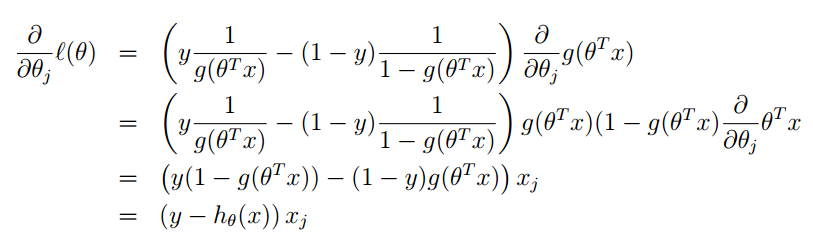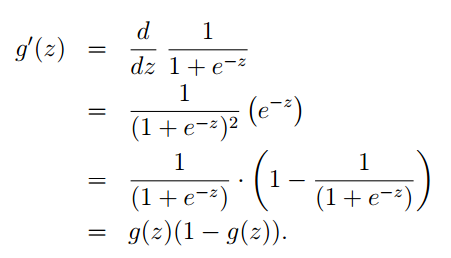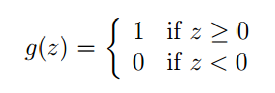转载自：https://blog.csdn.net/xiaocainiaodeboke/article/details/50371986

内容提要

这篇博客的主要内容有：
- 介绍欠拟合和过拟合的概念
- 从概率的角度解释上一篇博客中评价函数J(θ)” role=”presentation” style=”position: relative;”>J(θ)为什么用最小二乘法
- 局部加权线性回归（Locally Weighted Linear Regression (LWR)）
- 逻辑回归（Logistic regression）
- 感知器学习算法（The perceptron learning algorithm）

欠拟合与过拟合

我觉得欠拟合和过拟合都是从拟合的逼近训练集程度上说的。本身拟合就是对训练集特征提取的过程，那么就存在到底要精细到什么样的层次，这也就引出了欠拟合和过拟合的概念。这两个概念是相对的不是绝对的。
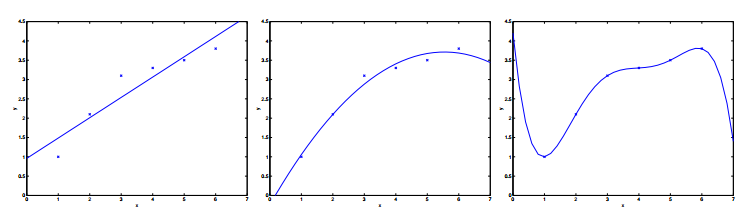
如下图：

对待同样的训练集我们可以用线性函数去拟合，也可以用二次，当然也可以用高次。三种拟合方式一次对应上面三幅图。Andrew Ng老师说就这个列子而言，第一种就是欠拟合，即拟合效果不好。第三种就是过拟合，同样拟合效果也不好。第二种是比较好的一个拟合。总之，拟合的效果好不好还是得靠实验结果。

为什么线性拟合的评价函数要用最小二乘法

回顾上一篇博客中讲的例子，我们现在可以把线性回归的模型写成下面的样子：

上标i” role=”presentation” style=”position: relative;”>i。为什么假设是正态分布，Andrew Ng老师解释说主要有两个原因：
- 一般的，训练集中的因素的都是独立的，而且对于某一种大量因素而言一般也都服从正态分布，比如我们的身高。根据中心极限定理（中心极限定理：设从均值为μ” role=”presentation” style=”position: relative;”>μ 的正态分布。）也可以证明。
- Andrew Ng老师说这样是为了计算的方便

根据y” role=”presentation” style=”position: relative;”>y的概率密度如下：

注意：这里的p(y(i)|x(i);θ)” role=”presentation” style=”position: relative;”>p(y(i)|x(i);θ)的概率。

我们将y(i)” role=”presentation” style=”position: relative;”>y(i)是已知的量，所以下面利用最大似然估计的思量，写出似然函数。

为了便于计算，我们对似然函数去对数，自然数为底。我们一般写成ln” role=”presentation” style=”position: relative;”>ln，表示的是一个意思。

减号前半部分都是常数，最大似然估计就是要让l(θ)” role=”presentation” style=”position: relative;”>l(θ)，去最大值。则就要求减号后面的部分取最小值。

这就证明了上篇博客中提到的评价函数的正确性。

局部加权线性回归（Locally Weighted Linear Regression (LWR)）

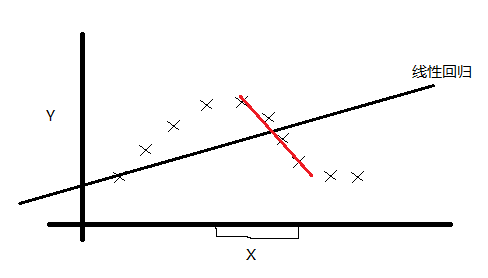
我们先来看下面训练集：

如果用我们之前的线性回归，显然是一个欠拟合。那么我们怎么改进呢?可能你想到了非线性回归，有人就想到了：采用局部线性回归的方式对上面的训练集进行拟合。经过实践，这种想法也是非常有效的。我们再来看看怎么用数学的方式体现局部拟合。我们的想法就是在线性回归的评价函数中添加一个具有局部性质的权重。如下：

其中的这个ω(i)” role=”presentation” style=”position: relative;”>ω(i)个训练样本的权重系数。这个权重系数具有下面的性质：
- 如果|x(i)−x|” role=”presentation” style=”position: relative;”>|x(i)−x|
- 如果|x(i)−x|” role=”presentation” style=”position: relative;”>|x(i)−x|

这个权重系数就可以提现局部特性了，式子中τ” role=”presentation” style=”position: relative;”>τ是波长参数，控制了权值随距离的下降速率，是一个实验参数。可能你觉得这个权重系数的表达是和正态分布的概率密度特别像，但是这里没有正态分布的这层含义。可能你也觉得选择其他的系数表达式可能更好，是的，这的确存在争议，但是一般情况下选择这个系数表达式，拟合效果比较好。当然你也可以具体情况具体分析。

上面这些如何选择系数表达式，你可能不太在意。可能比较纠结ω(i)” role=”presentation” style=”position: relative;”>ω(i),这时就可以预测房价了。

总结一下：LWR算法是我们遇到的第一个non-parametric（非参数）学习算法，而线性回归则是我们遇到的第一个parametric（参数）学习算法。所谓参数学习算法它有固定的明确的参数，参数一旦确定，就不会改变了，我们不需要在保留训练集中的训练样本。而非参数学习算法，每进行一次预测，就需要重新学习一组，θ” role=”presentation” style=”position: relative;”>θ向量是变化的，所以需要一直保留训练样本。也就是说，当训练集的容量较大时，非参数学习算法需要占用更多的存储空间，计算速度也较慢。有得必有失，效果好当然要牺牲一些其他的东西。

逻辑回归（Logistic regression）

我们先看一个训练集，如下图：

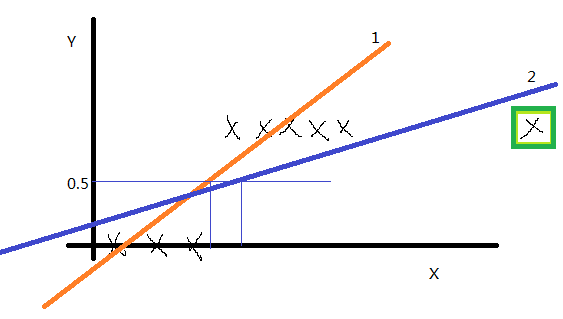
如果y” role=”presentation” style=”position: relative;”>y的取值只有0和1，训练集画出来这这个样子（先没有绿框中的点），我们用线性回归得到1号直线，如果认为模拟直线的取值小于0.5时则预测值就为0，如果模拟直线的取值大于0.5时预测值就为1，感觉还不错。但是将绿框中的点加入后，线性回归得到的直线2，就显得不是很完美了。经过大量的实验证明，线性回归不适合这种训练集。那么怎么解决这个问题呢？

我们提出来了一种新的回归模型：

其中g” role=”presentation” style=”position: relative;”>g的函数原型为：

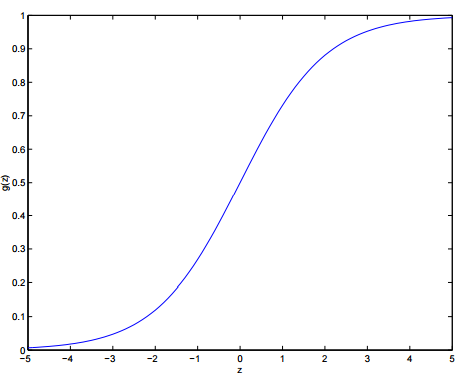
它的图像为：

可以看出：
- 当z>0” role=”presentation” style=”position: relative;”>z>0
- 当z<0” role=”presentation” style=”position: relative;”>z<0

g(z)” role=”presentation” style=”position: relative;”>g(z)这个函数称之为：logistic function 或者 sigmoid function
利用g(z)” role=”presentation” style=”position: relative;”>g(z)函数，我们做出如下假设：

同样的这里P(y=1|x;θ)” role=”presentation” style=”position: relative;”>P(y=1|x;θ)并不是表示条件概率，是一种类似最大似然估计的表示方式，表示出参数。也可以将他们写在一块，如下：

你可以把y” role=”presentation” style=”position: relative;”>y的值带入验证，结果是正确的。

我们还是利用最大似然估计的思想去求参数，先构造似然函数。

然后去对数：

最大似然估计就是要让l(θ)” role=”presentation” style=”position: relative;”>l(θ)的梯度就可以了：

其中对于g(θTx)” role=”presentation” style=”position: relative;”>g(θTx)的求导可以参考下面：

总结一下：逻辑回归，和线性回归其本质思想上是一致的。都是利用概率的思想，把我们的估计值当成一个随机变量，我们的训练集就是一组抽样。之后再利用最大似然估计，求其中的参数。当其中的参数求出来后，我们也就得到了回归方程，就可以进行预测或者其他工作了。

感知器学习算法（The perceptron learning algorithm）

这个算法是对逻辑回归的强行约束，使得函数值取0和1。定义形式如下：

同样的我们假设hθ(x)=g(θTx)” role=”presentation” style=”position: relative;”>hθ(x)=g(θTx)向量。整个推导过程和逻辑回归一样，最终结果如下：

总结

现在我已经学习的梯度下降算法属于参数学习算法，局部加权线性回归属于非参数学习算法，感知器学习算法属于聚类算法。他们都属于监督学习这个大类。

end

        <link rel="stylesheet" href="https://csdnimg.cn/release/phoenix/template/css/markdown_views-ea0013b516.css">
            </div>

内容提要

欠拟合与过拟合

为什么线性拟合的评价函数要用最小二乘法

回顾上一篇博客中讲的例子，我们现在可以把线性回归的模型写成下面的样子：

根据y” role=”presentation” style=”position: relative;”>y的概率密度如下：

注意：这里的p(y(i)|x(i);θ)” role=”presentation” style=”position: relative;”>p(y(i)|x(i);θ)的概率。

我们将y(i)” role=”presentation” style=”position: relative;”>y(i)是已知的量，所以下面利用最大似然估计的思量，写出似然函数。

为了便于计算，我们对似然函数去对数，自然数为底。我们一般写成ln” role=”presentation” style=”position: relative;”>ln，表示的是一个意思。

减号前半部分都是常数，最大似然估计就是要让l(θ)” role=”presentation” style=”position: relative;”>l(θ)，去最大值。则就要求减号后面的部分取最小值。

这就证明了上篇博客中提到的评价函数的正确性。

局部加权线性回归（Locally Weighted Linear Regression (LWR)）

我们先来看下面训练集：

上面这些如何选择系数表达式，你可能不太在意。可能比较纠结ω(i)” role=”presentation” style=”position: relative;”>ω(i),这时就可以预测房价了。

逻辑回归（Logistic regression）

我们先看一个训练集，如下图：

我们提出来了一种新的回归模型：

其中g” role=”presentation” style=”position: relative;”>g的函数原型为：

它的图像为：

可以看出：
- 当z>0” role=”presentation” style=”position: relative;”>z>0
- 当z<0” role=”presentation” style=”position: relative;”>z<0

你可以把y” role=”presentation” style=”position: relative;”>y的值带入验证，结果是正确的。

我们还是利用最大似然估计的思想去求参数，先构造似然函数。

然后去对数：

最大似然估计就是要让l(θ)” role=”presentation” style=”position: relative;”>l(θ)的梯度就可以了：

其中对于g(θTx)” role=”presentation” style=”position: relative;”>g(θTx)的求导可以参考下面：

感知器学习算法（The perceptron learning algorithm）

这个算法是对逻辑回归的强行约束，使得函数值取0和1。定义形式如下：

同样的我们假设hθ(x)=g(θTx)” role=”presentation” style=”position: relative;”>hθ(x)=g(θTx)向量。整个推导过程和逻辑回归一样，最终结果如下：

总结

end

        <link rel="stylesheet" href="https://csdnimg.cn/release/phoenix/template/css/markdown_views-ea0013b516.css">
            </div>

斯坦福Andrew Ng---机器学习笔记（二）：Logistic Regression(逻辑回归)

内容提要

欠拟合与过拟合

为什么线性拟合的评价函数要用最小二乘法

局部加权线性回归（Locally Weighted Linear Regression (LWR)）

逻辑回归（Logistic regression）

感知器学习算法（The perceptron learning algorithm）

总结

内容提要

欠拟合与过拟合

为什么线性拟合的评价函数要用最小二乘法

局部加权线性回归（Locally Weighted Linear Regression (LWR)）

逻辑回归（Logistic regression）

感知器学习算法（The perceptron learning algorithm）

总结

猜你喜欢