【算法设计-分治、动态规划】递归与尾递归

1. 阶乘

输入一个整数 n，输出 n 的阶乘。

传统的递归写法：

#include <cstdio>
using namespace std;

long long func (int n){
    
    
	if (n == 0 || n == 1)
		return 1;
	else
		return n * func(n-1);
}

int main(){
    
    
	int n;
	while (scanf("%d", &n) != EOF){
    
    
		long long answer = func(n);
		printf("%lld\n", answer);
	}
	return 0;
}

若 n=5，递归过程如下：

• 调用 func(5)
• 调用 func(5) 后：5 * func(4)
• 调用 func(4) 后：5 * (4 * func(3))
• 调用 func(3) 后：5 * (4 * (3 * func(2)))
• 调用 func(2) 后：5 * (4 * (3 * (2 * func(1))))
• 调用 func(1) 后：5 * (4 * (3 * (2 * 1)))
• 返回到 func(2) ：5 * (4 * (3 * 2))
• 返回到 func(3) ：5 * (4 * 6)
• 返回到 func(4) ：5 * 24
• 返回到 func(5) ：120

可以看到，如果采用以上写法，那么要调用到func(1)时才能得到最终的计算式，所以程序需要记住诸如5 * (4 * (3 *…的内容，也即，之前的func(5)到func(2)的帧必须存储。这意味着，当 n 比较大的时候，程序运行时间比较长，以及占用大量的栈帧。

尾递归：递归的进一步优化

如果我们能一边调用，一边计算，那就不用存储中间的函数栈帧，就能大大加快程序的执行效率，因此可采用一种尾递归优化的技术。

如果一个函数中所有递归形式的调用都出现在函数的末尾，我们称这个递归函数是尾递归的。采用尾递归的写法，可防止大量的内存浪费。

把以上定义翻译成人话，就可以得出尾递归的特征：返回语句return除了返回函数自身以外，不再执行任何指令或语句。关于尾递归的详细原理，可参见：尾递归原理。

按照以上特征来判断：上面的代码是尾递归吗？看起来像，但其实不是，因为上面的代码可以等价成如下代码：

#include <cstdio>
using namespace std;

long long func (int n){
    
    
	if (n == 0 || n == 1)
		return 1;
	else{
    
    
	    long long tmp = func(n-1); // 先调用函数自身
	    return n * tmp;            // 再进行乘法运算
	}                              // 递归调用没有出现在函数的末尾，因此不是尾递归
}

int main(){
    
    
	int n;
	while (scanf("%d", &n) != EOF){
    
    
		long long answer = func(n);
		printf("%lld\n", answer);
	}
	return 0;
}

这才是真正的尾递归：

#include <cstdio>
using namespace std;

long long func1 (int n, int result){
    
    
	if (n == 0 || n == 1)
		return result;
	else
		return func1(n-1, result*n);   // 计算结果传递给下一次递归调用
}

int main(){
    
    
	int n;
	while (scanf("%d", &n) != EOF){
    
    
		long long answer = func1(n, 1);
		printf("%lld\n", answer);
	}
	return 0;
}

若 n=5，递归过程如下：

• func1(5,1)
• func1(4,5)
• func1(3,20)
• func1(2,60)
• func1(1,120)

可以看到，当进行尾递归优化后，程序不需要存储每一个函数的栈帧。而且还应当注意到，传统的递归是调用到最内层时才得知边界条件，而尾递归是在开始调用函数时就已经得知初值或边界条件，这是一个重要的特征，在下面几个例子中，我希望大家可以好好体会这一点。

再次提醒，在传统的递归中，程序为什么要存储那么多函数栈帧？不就是因为函数调用完递归后还有别的操作嘛（在这里就是存储func(5)到func(2)的帧，因为这些帧都还没运行完）。现在采用尾递归，每一次调用都可以算出结果，而且每次计算结果都会成为下一次调用的参数，更重要的是，当程序调用自身运行完毕后，这个函数已经没有其他执行语句了。那程序还有必要存储当下的函数栈帧吗？没必要了。事实上，程序在每次调用尾递归后，上一次的函数栈帧都会被覆盖。

最后，这里应该无内鬼吧，那就来点知乎段子：

function story() {
    
        
从前有座山，山上有座庙，庙里有个老和尚，一天老和尚对小和尚讲故事：story() 
// 尾递归，进入下一个函数不再需要上一个函数的环境了，得出结果以后直接返回。
}

function story() {
    
        
从前有座山，山上有座庙，庙里有个老和尚，一天老和尚对小和尚讲故事：story()，小和尚听了，找了块豆腐撞死了 
// 非尾递归，下一个函数结束以后此函数还有后续，所以必须保存本身的环境以供处理返回值。
}

【注1】在严重依赖递归的函数式编程（比如Lisp）和逻辑式编程（比如Prolog）中，尾递归优化非常重要，可以大大减轻程序运行的负担。

【注2】建议不要太纠结于递归的具体运行过程。相较于传统的手把手教电脑做事的命令式编程，递归更像是声明式编程，给一个函数递推式或几条规则，电脑就可以自己一路算下去了，颇有早期人工智能的感觉。人工智能的本质就是一个黑箱，比如神经网络、深度学习，经过上千万次训练后电脑自己就学会了，你不知道、甚至不必去理解黑箱里是怎么实现的，如果接触过Prolog和Lisp语言，对这一点会有更深的体会。所以，我个人觉得可以将递归视为一个黑箱子，不要太过纠结于递归的具体运行过程。

2. 斐波那契数列

已知斐波那契数列的递推式f(n) = f(n-1) + f(n-2)，初值f(1)=1, f(2)=1，输入一个整数 n，输出 f(n) 的值。

传统的递归写法：

#include <cstdio>
using namespace std;

long long func (int n){
    
    
	if (n == 0 || n == 1 || n == 2)
		return 1;
	else
		return func(n-1) + func(n-2);
}

int main(){
    
    
	int n;
	while (scanf("%d", &n) != EOF){
    
    
		long long answer = func(n);
		printf("%lld\n", answer);
	}
	return 0;
}

以上是尾递归吗？不是，因为可以等价为如下代码：

#include <cstdio>
using namespace std;

long long func (int n){
    
    
	if (n == 1 || n == 2)
		return 1;
	else{
    
    
	    long long a = func(n-1);
	    long long b = func(n-2);  // 实际上到这一步就已经不是尾递归了，因为还要再使用一次n的值，
	                              // 这就要求程序把该函数的栈帧保留下来
	    return a + b;
	}
}

int main(){
    
    
	int n;
	while (scanf("%d", &n) != EOF){
    
    
		long long answer = func(n);
		printf("%lld\n", answer);
	}
	return 0;
}

现在请进行尾递归优化：

#include <cstdio>
using namespace std;

long long func1 (int n, int f1, int f2){
    
      // f1: f(n-2), f2: f(n-1)
	if (n == 1 || n == 2)
		return f2;
	else
		return func1(n-1, f2, f1+f2);  // f2: f(n-1), f1+f2: f(n)
}

int main(){
    
    
	int n;
	while (scanf("%d", &n) != EOF){
    
    
		long long answer = func1(n, 1, 1); // init: f(1)=1, f(2)=1
		printf("%lld\n", answer);
	}
	return 0;
}

实际上，当 n 非常非常大时，该代码的执行效率也会下降。若想快速算出 f(n)，请使用矩阵快速幂算法，在本人的算法专栏里已有涉及。

3. 最大公约数（GCD）

辗转相除法：两个整数的最大公约数等于其中较小的数和两数相除的余数的最大公约数，即gcd(a,b) = gcd(b, a mod b)。

基本思想：分治。

原理：若整数 g 为 a、b 的最大公约数，则有：

a = g x l（1）

b = g x m（2）

a、b 又可以表示为：

a = b x k + r（即a / b = k···r）（3）

把（1）（2）代入到（3）：

g x l = g x m x k + r，即r = g x (l - m x k)

注意到r = a mod b，因此a mod b = g x (l - m x k)（4）

联合（2）（4），这样问题变为了求 b 和 a mod b 的最大公约数：

b = g x m（2）

a mod b = g x (l - m x k)（5）

代码实现：

// 辗转相除法求最大公约数（12和18的最大公约数：6） 
int gcd (int a, int b){
    
    
    if (b == 0)
        return a;
    else
        return gcd(b, a % b);
}

很明显，这是一个尾递归。

4. 上楼梯

楼梯有 n 级台阶（n ≤ 20），可以一步走 1 级，也可以一步走 2 级。请计算一共有多少种不同的走法。

分析：1 级台阶只有一种走法，2 级台阶有两种走法（1+1, 2），3 级台阶有三种走法（1+1+1,2+1,1+2）。

从另一个角度思考，我们采用分治思想：

• 到第 n 级台阶有两种方法，一种是从 n-1 级台阶走一步就到，一种是从 n-2 级台阶走两步就到；
• 所以，走到第 n 级台阶的方法总数等于走到 n-1 级台阶的方法总数加上走到 n-2 级台阶的方法总数；
• 那到第 n-1 级台阶的方法总数怎么算呢？首先考虑这两种方法，一种是从 n-2 级台阶走一步就到，一种是从 n-3 级台阶走两步就到；
• 所以，走到第 n-1 级台阶的方法总数等于走到 n-2 级台阶的方法总数加上走到 n-3 级台阶的方法总数；
• 那到第 n-2 级台阶的方法总数怎么算呢？首先考虑这两种方法，一种是从 n-3 级台阶走一步就到，一种是从 n-4 级台阶走两步就到；
• 所以，走到第 n-2 级台阶的方法总数等于走到 n-3 级台阶的方法总数加上走到 n-4 级台阶的方法总数；
• …

因此，该问题实质上是一个变形的斐波那契数列，递推式f(n) = f(n-1) + f(n-2)，初值f(1)=1, f(2)=2。

代码如下：

#include <cstdio>
using namespace std;

long long func1 (int n, int f1, int f2){
    
      // f1: f(n-2), f2: f(n-1)
	if (n == 1 || n == 2)
		return f2;
	else
		return func1(n-1, f2, f1+f2);  // f2: f(n-1), f1+f2: f(n)
}

int main(){
    
    
	int n;
	while (scanf("%d", &n) != EOF){
    
    
		long long answer = func1(n, 1, 2); // init: f(1)=1, f(2)=2
		printf("%lld\n", answer);
	}
	return 0;
}

5. 汉诺塔（1）

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

输出移动过程

现在用 A、B、C 表示这三个柱子，输入盘子总数 n，请输出每一次的移动过程。

输入和输出：

3
第1个盘子移动：A->C
第2个盘子移动：A->B
第1个盘子移动：C->B
第3个盘子移动：A->C
第1个盘子移动：B->A
第2个盘子移动：B->C
第1个盘子移动：A->C

分析：若只有一个盘子，从 A 移到 C；若只有两个盘子，小盘子从 A 移到 B，大盘子从 A 移到 C，小盘子从 B 移到 C。

现在考虑 n (n ≥ 3) 个盘子的情况。我们使用分治递归思想，看看能不能将问题变得更简单一些。几个问题：

• 移动的目的是什么？或者说我们想达成什么目标？我们要想把 n 个盘子全部转移到 C，那么我们可以将底下最大的盘子先转移到 C 柱，因为一旦最大的盘子移了过去，剩下 n-1 个盘子就可以无视这个最大的盘子，进行下一次移动了。
• 这剩余 n-1 个盘子是不是又可以这样：将底下次大的盘子先转移到 C 柱，剩下的 n-2 个盘子就可以无视次大的盘子，又可以进行下一次移动了。
• 怎么达成该目的？可以把 n 个盘子视为两组，一组是最大的盘子，另一组是剩余 n-1 个盘子。从宏观上看，我们可以把这两组视为两个“大盘子”。这样问题就回到了移动两个盘子的情况，我们按两个盘子的方法移动就行了。
• 但实际上这 n-1 个盘子是不能直接移动的，那我们是不是又可以把这 n-1 个盘子视为两个“大盘子”，一组是次大的盘子，另一组是剩余 n-2 个盘子，这样就又回到了移动两个盘子的情况。

因此通过这样的思考，得出将 n 个盘子从 A 移到 C 的步骤或规则，实际上跟两个盘子的移动方法是完全一致的：

• 将 n-1 个盘子从 A 移到 B，实质上就是将 C 当成缓冲区；
• 将第 n 个盘子（也是最大的盘子）从 A 移到 C，实质上就是将 B 当成缓冲区；
• 将 n-1 个盘子从 B 移到 C，实质上就是将 A 当成缓冲区。

将步骤或规则用代码实现如下：

#include <cstdio>
using namespace std;

void func (int n, char init, char buffer, char dist){
    
      
	if (n == 0){
    
    
		return;
	}
	else if (n == 1){
    
    
		printf("第%d个盘子移动：%c->%c\n", n, init, dist);
		return;
	}
	else{
    
    
		func(n-1, init, dist, buffer);  
		printf("第%d个盘子移动：%c->%c\n", n, init, dist);
		func(n-1, buffer, init, dist);
	}		 
}

int main(){
    
    
	int n;
	while (scanf("%d", &n) != EOF){
    
    
		func(n, 'A', 'B', 'C'); 
	}
	return 0;
}

请读者注意，这里是探讨算法的文章，不是探讨编程语言的特性，除了在讨论尾递归时我们不得不关注程序运行的细节以外，其余代码不必过分关注运行细节，请把目光放在如何思考得出步骤和规则这件事上来！

输出移动步数

输入盘子总数 n，请输出所需移动步数。

分析：结合以上步骤可得出递推式。

• 将 n-1 个盘子从 A 移到 B，需要的移动次数设为f(n-1)；
• 将第 n 个盘子从 A 移到 C，需要的移动次数为 1；
• 将 n-1 个盘子从 B 移到 C，需要的移动次数依然为f(n-1)。

所以递推式为f(n) = 2f(n-1) + 1。

接下来考虑初值情况，从 A 到 B 移动需 1 次，所以易知f(1) = 1, f(2) = 3，n=2 时正好与递推式算得的结果相吻合。

代码实现如下：

long long func1 (int n){
    
    
	if (n == 0)
		return 0;
	else if (n == 1)
		return 1;
	else
		return 2 * func1(n-1) + 1;
}

进行尾递归优化后：

long long func2 (int n, long long result = 1){
    
    
	if (n == 0)
		return 0;
	else if (n == 1)
		return result;
	else
		return func2(n-1, 2*result+1);
}

5. 汉诺塔（2）

输出移动过程

问题改变！现在不允许将盘子从 A 移到 C，且不允许从 C 移到 A。输入盘子总数 n，请输出每一次的移动过程。

输入和输出：

2
第1个盘子移动：A->B
第1个盘子移动：B->C
第2个盘子移动：A->B
第1个盘子移动：C->B
第1个盘子移动：B->A
第2个盘子移动：B->C
第1个盘子移动：A->B
第1个盘子移动：B->C

分析：只有一个盘子，从 A 移到 B，从 B 移到 C；只有两个盘子，小盘子从 A 移到 B、从 B 移到 C，大盘子从 A 移到 B，小盘子从 C 移到 B、从 B 移到 A，大盘子从 B 移到 C，小盘子从 A 移到 B、从 B 移到 C。

继续使用分治思想，将 n 个盘子从 A 移到 C 的步骤与两个盘子是类似的：

• 将 n-1 个盘子从 A 移到 B；
• 将 n-1 个盘子从 B 移到 C；
• 将第 n 个盘子（也是最大的盘子）从 A 移到 B；
• 将 n-1 个盘子从 C 移到 B；
• 将 n-1 个盘子从 B 移到 A；
• 将第 n 个盘子（也是最大的盘子）从 B 移到 C；
• 将 n-1 个盘子从 A 移到 B；
• 将 n-1 个盘子从 B 移到 C。

以上步骤等价于：

• 将 n-1 个盘子从 A 移到 C，实质上就是将 B 当成缓冲区；
• 将第 n 个盘子（也是最大的盘子）从 A 移到 B，实质上就是将 C 当成缓冲区；
• 将 n-1 个盘子从 C 移到 A，实质上就是将 B 当成缓冲区；
• 将第 n 个盘子（也是最大的盘子）从 B 移到 C，实质上就是将 A 当成缓冲区；
• 将 n-1 个盘子从 A 移到 C，实质上就是将 B 当成缓冲区。

代码如下：

#include <cstdio>
using namespace std;

void func (int n, char init, char buffer, char dist){
    
      
	if (n == 0){
    
    
		return;
	}
	else if (n == 1){
    
    
		printf("第%d个盘子移动：%c->%c\n", n, init, buffer);
		printf("第%d个盘子移动：%c->%c\n", n, buffer, dist);
		return;
	}
	else{
    
    
		func(n-1, init, buffer, dist);
		printf("第%d个盘子移动：%c->%c\n", n, init, buffer);
		func(n-1, dist, buffer, init);
		printf("第%d个盘子移动：%c->%c\n", n, buffer, dist);
		func(n-1, init, buffer, dist);
	}		 
}

int main(){
    
    
	int n;
	while (scanf("%d", &n) != EOF){
    
    
		func(n, 'A', 'B', 'C'); 
	}
	return 0;
}

输出移动步数

输入盘子总数 n，请输出所需移动步数。

分析：结合以上步骤可得出递推式。

• 将 n-1 个盘子从 A 移到 C，需要的移动次数设为f(n-1)；
• 将第 n 个盘子从 A 移到 B，需要的移动次数为 1；
• 将 n-1 个盘子从 C 移到 A，需要的移动次数依然为f(n-1)；
• 将第 n 个盘子从 B 移到 C，需要的移动次数为 1；
• 将 n-1 个盘子从 A 移到 C，需要的移动次数依然为f(n-1)。

所以递推式为f(n) = 3f(n-1) + 2。

接下来考虑初值情况，从 A 到 C 移动需 2 次，所以易知f(1) = 2, f(2) = 8，n=2 时正好与递推式算得的结果相吻合。

有读者可能会觉得奇怪，为什么把“从 A 到 C”的移动次数设为f(n-1)，而不把“从 A 到 B”或“从 B 到 C”的移动次数设为f(n-1)，其实这样假设也没有什么区别，只是递推式不一样，但得出的结果肯定是一样的，我们来看看吧！

• 将 n-1 个盘子从 A 移到 B，需要的移动次数设为f(n-1)；
• 将 n-1 个盘子从 B 移到 C，需要的移动次数依然为f(n-1)；
• 将第 n 个盘子从 A 移到 B，需要的移动次数为 1；
• 将 n-1 个盘子从 C 移到 B，需要的移动次数依然为f(n-1)；
• 将 n-1 个盘子从 B 移到 A，需要的移动次数依然为f(n-1)；
• 将第 n 个盘子从 B 移到 C，需要的移动次数为 1；
• 将 n-1 个盘子从 A 移到 B，需要的移动次数依然为f(n-1)；
• 将 n-1 个盘子从 B 移到 C，需要的移动次数依然为f(n-1)。

所以递推式为f(n) = 6f(n-1) + 2。

接下来考虑初值情况，从 A 到 B 移动仅需 1 次，所以易知f(1) = 1, f(2) = 8，n=2 时与递推式算得的结果也相吻合。

最后使用代码实现如下：

代码实现如下：

long long func1 (int n){
    
    
	if (n == 0)
		return 0;
	else if (n == 1)
		return 2;
	else
		return 3 * func1(n-1) + 2;
}

进行尾递归优化后：

long long func2 (int n, long long result = 2){
    
    
	if (n == 0)
		return 0;
	else if (n == 1)
		return result;
	else
		return func2(n-1, 3*result+2);
}

6. 杨辉三角形

输入行数 n，输出 n 行杨辉三角形。

输入和输出：

8
  1
  1   1
  1   2   1
  1   3   3   1
  1   4   6   4   1
  1   5  10  10   5   1
  1   6  15  20  15   6   1
  1   7  21  35  35  21   7   1
10
  1
  1   1
  1   2   1
  1   3   3   1
  1   4   6   4   1
  1   5  10  10   5   1
  1   6  15  20  15   6   1
  1   7  21  35  35  21   7   1
  1   8  28  56  70  56  28   8   1
  1   9  36  84 126 126  84  36   9   1

分析：注意到第 n 行第 1 个元素和第 n 个元素均为 1，其余元素都是由递推式A[i][j] = A[i-1][j-1] + A[i-1][j]得来。

递归代码：

#include <cstdio>
using namespace std;

int YH (int i, int j){
    
    
	if (j == 1 || i == j)
		return 1;
	else 
		return YH(i-1, j-1) + YH(i-1, j);
}

int main(){
    
    
	int n;
	while (scanf("%d", &n) != EOF){
    
    
		for (int i = 1; i <= n; i++){
    
    
			for (int j = 1; j <= i; j++){
    
    
				printf("%3d ", YH(i, j));
			}
			printf("\n");
		}
	}
	return 0;
}

7. 完全二叉树

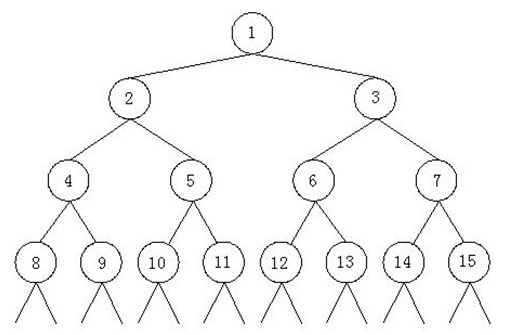
【描述】如上所示，由正整数1，2，3……组成了一颗特殊二叉树。我们已知这个二叉树的最后一个结点是n。现在的问题是，结点m所在的子树中一共包括多少个结点。

比如，n = 12，m = 3那么上图中的结点13，14，15以及后面的结点都是不存在的，结点m所在子树中包括的结点有3，6，7，12，因此结点m的所在子树中共有4个结点。

【输入描述】输入数据包括多行，每行给出一组测试数据，包括两个整数m，n (1 <= m <= n <= 1000000000)。

【输出描述】对于每一组测试数据，输出一行，该行包含一个整数，给出结点m所在子树中包括的结点的数目。

【输入示例】

3 12
0 0

【输出示例】

4

【分析】求结点 m 所在子树总结点数，就是在求结点 m 的左子树总结点数和右子树总结点数，还要加上自身结点。

注意，对于一棵完全二叉树，结点 m 的左子树结点编号为 2m，结点 m 的右子树结点编号为 2m+1。

边界条件：当 m > n 时，结点 m 所在子树总结点数为 0。

【题解】

#include <cstdio>
using namespace std;

// m：结点编号，n：总结点数 
int func (int m, int n){
    
    
	if (m > n)
		return 0;
	else 
		return 1 + func(2*m, n) + func(2*m+1, n);
}

int main(){
    
    
	int m, n;
	while (scanf("%d %d", &m, &n) != EOF){
    
    
		printf("%d\n", func(m, n));
	}
	return 0;
}