算法分析与设计：递归与分治策略

1、递归

定义：递归算法是一个过程或函数在其定义或说明中又直接或间接调用自身的一种方法。
递归算法可以将一个大型的复杂问题转化为一个与原问题相似的规模较小的问题求解，其优势在于用有限的语句定义无限的集合，可以有效减少代码量，使程序简洁易懂；其缺点在于运行效率低，空间消耗大，容易造成堆栈溢出。
递归需要有边界条件，递归前进段和递归返回段。当不满足边界条件时，递归前进；当满足边界条件时，递归返回。递归必须有一个明确的边界条件，又称为递归出口，否则递归将无限进行下去。
递归算法适用的3类问题：

数据的定义是递归定义的。例如Ackerman函数；
问题解法用递归算法实现。例如回溯算法；
数据结构的形式是递归定义的。如树的遍历。

具有递归特性的问题

(1) 阿克曼函数
阿克曼函数的数学定义如下：

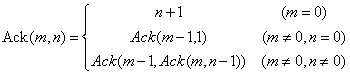
阿克曼函数的算法描述如下：

int ack(int n,int m)
{
    if(m == 0)
        return n + 1;
    else if(n == 0)
        return ack(m - 1,n);
    else
        return ack(m - 1,ack(m,n - 1));
}

(2) 斐波那契数列
斐波那契数列又称黄金分割数列，其头两项均为1；从第三项开始，每一项都等于前两项之和。
斐波那契数列的数学定义如下：

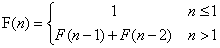
斐波那契数列的递归算法描述如下：

int fibo(int n)
{
    if(n <= 1)
        return 1;
    else
        return fibo(n - 1) + fibo(n - 2);
}

斐波那契数列也可以用转化为递推问题。递推算法描述如下：

int fibo(int n)
{
    int f[n];
    f[0] = f[1] = 1;
    for(int i = 2;i < n;i++)
        f[i] = f[i - 1] + f[i - 2];
    return f[n - 1];
}

(3) 汉诺塔问题
汉诺塔问题可以概括为：某处有三个柱子A，B，C；在柱子A上有64个圆盘的，并且大圆盘在下，小圆盘在上；若一次只能搬动一个圆盘，且搬动过程始终保持大圆盘在下，小圆盘在上。如何搬动才能将柱子A上的圆盘全部转移到柱子B上？
分析：
如果只有一个圆盘，那只需要将它从A搬到B，即可完成；
如果有两个圆盘，那需要先将上方圆盘搬到C，再将下方圆盘搬到B，最后将C上的圆盘搬到B上，即可完成；
如果有三个圆盘，那需要先将上方两个圆盘搬到C，再将最下方圆盘搬到B，最后将上方两个圆盘搬到B，即可完成；
以此类推：对于n个圆盘，先将上方的n-1个圆盘搬到C，再将最下方圆盘搬到B，最后将上方n-1个圆盘搬到B，即可完成。
由此，可得汉诺塔问题的递归算法描述如下：

//move函数的作用是将第一个柱子的第一个圆盘搬到第二个柱子上
void hanoi(int n,char a,char b,char c)	//a为起始柱，b为目标柱，c为中间柱
{
    if(n == 1)  move(a,b);
    else{
        hanoi(n - 1,a,c,b);
        move(a,b);
        hanoi(n - 1,c,b,a);
    }
}

递归算法分析

设递归算法的时间复杂度为T(n)，每次可以将问题划分为a个规模为原来1/b的子问题，且每次划分和重组的花费为d(n)。
当n=1时为递归出口，此时时间复杂度为1；
由此可以计算递归算法的时间复杂度：
T(n)展开
设n = bⁱ，有：
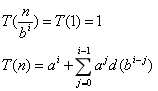
n=bi的情形
设d(x)为积性函数，即d(x*y)=d(x)*d(y)，有：
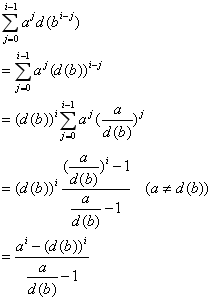
扩展后半部分
若a > d(b)，则有：

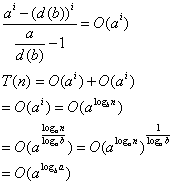
若a < d(b)，则有：

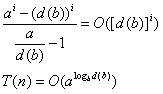
若a = d(b)，则有：

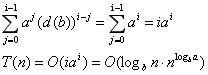
以快速排序算法为例

快速排序的具体算法描述如下：

template<class T>
int Partition(T *p,int low,int high)
{
    T pivot = p[low];     //获取枢轴
    //p[0] = p[low];          //暂存枢轴
    while(low < high){      //两端扫描并划分
        while(low < high && p[high] >= pivot)
            --high;
        p[low] = p[high];
        while(low < high && p[low] <= pivot)
            ++low;
        p[high] = p[low];
    }
    p[low] = pivot;          //记录枢轴
    return low;             //返回枢轴位置
}

template<class T>
void QuickSort(T *p,int low,int high)
{
    if(low < high){         //递归出口
        int pivot = Partition(p,low,high);  //第一次划分
        QuickSort(p,low,pivot-1);   //对左边递归
        QuickSort(p,pivot+1,high);  //对右边递归
    }
}

其a=2，b=2，d(n)=n为积性函数，且a = d(b) = 2；
由此可知，快速排序的时间复杂度为：
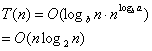
快速排序时间复杂度

2、分治策略

分治策略(又称分治法)是对于一个规模为n的问题，若该问题可以容易地解决则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同。分治策略递归地解这些子问题，再将各个子问题的解合并得到原问题的解。

分治法的基本步骤：

分解：将原问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题；
解决：若子问题规模较小而容易解决则直接解，否则递归地解；
合并：将各子问题的解合并为原问题的解。
合并是分治法的关键所在，需要具体问题具体分析。

分治法的适用条件：

该问题缩小到一定程度可以容易地解决；
该条件对于绝大多数问题能够满足。
该问题可以分解为若干个规模较小的相同子问题，即问题具有最优子结构性质；
该条件是应用分治法的前提，也是大多数问题可以满足的，反映了递归思想的应用。
利用该问题分解出的子问题可以合并为该问题的解；
能否利用分治法完全取决于该条件。若具备条件1、2而不具备条件3，可以考虑动态规划法或贪心法。
该问题的各个子问题是独立的，不包含公共子问题。
该条件涉及分治法的效率。若各子问题不是独立的，则分治法需要很多不必要的工作。

分治策略往往和递归算法同时使用，因此递归算法的时间复杂度分析可适用于分治法。

应用分治法解决问题举例

上面介绍递归算法的时间复杂度计算时举例的快速排序也是分治法的一种应用。

(1) 二分查找法
给定n个元素组成的有序序列{0:n-1]，在这n个元素中找到特定元素x。若使用顺序查找法，最坏情况下的时间复杂度为O(n)；
利用有序的条件，采用二分查找法可以在最坏情况下将时间复杂度减少到O(log n)。

二分查找法的基本思想是：

将n个元素分成两半，取a[n/2[与x比较；若x = a[n/2[，则找到对应元素，查找结束；
若x <a[n/2]，则在数组的左半部分继续查找；否则在右半部分继续查找；
无法再划分时，查找失败；

二分查找法的算法描述如下：

int binarySearch(int a[],int x,int n)
{
    int low = 0;
    int high = n - 1;
    while(low <= high){
        int middle = (low + high) / 2;
        if(a[middle] == x)
            return middle;
        else if(x < a[middle])
            high = middle - 1;
        else
            low = middle + 1;
    }
    return -1;
}

每次while循环都将待查找的数组减小了一半，因此在最坏情况下，while循环执行了O(log n)次,而循环体内的执行时间为O(1)，因此二分查找法在最坏情况下的时间复杂度为O(log n)。

(2) 棋盘覆盖问题
在一个2^k * 2^k 个方格组成的棋盘中，若恰有一个与其他方格不同，称该方格为特殊方格，且称该棋盘为特殊棋盘。要求用4种不同形状(方向不同)的L型骨牌覆盖棋盘上除特殊方格以外的所有方格，且L型骨牌不得重叠覆盖。显然，在任何一个棋盘中，使用的L型骨牌个数为(4^k-1)/3。

使用分治策略可以得到棋盘覆盖问题的一个简捷的算法。算法基本思想如下：

沿棋盘的两条对称线，将棋盘划分为4个2^k-1 * 2^k-1 个方格组成的子棋盘；划分后，4个子棋盘中将有一个棋盘为特殊棋盘，剩余的棋盘中均不包含特殊方格。
为了将三个普通棋盘转化为普通方格，将三个棋盘的汇合处（即原棋盘中点附近四个方格中的三个）用一个L型骨牌覆盖，并在子棋盘中将它们看作特殊方格；
重复使用这种分治策略，直至棋盘划分为11的子棋盘，则三个11子棋盘的方格可以用一个L型骨牌覆盖，即棋盘覆盖完成。

棋盘覆盖问题的分治算法描述如下：

int board[1025][1025];//为方便递归，将棋盘设为全局变量，其中[0][0]表示左上角方格。
static int title = 1;//使用的骨牌编号

void chessboard(int tr,int tc,int dr,int dc,int size)//tr,tc表示棋盘的左上角坐标；dr,dc表示特殊方格坐标;size表示棋盘大小
{
    if(size == 1)   return;
    int s = size / 2;
    int t = title++;
    if(dr < tr + s && dc < tc + s) //特殊方格在左上角棋盘
        chessboard(tr,tc,dr,dc,s);
    else{//不在左上角棋盘，使用t号骨牌覆盖右下角方格
        board[tr + s - 1][tc + s - 1] =t;
        chessboard(tr,tc,tr+s-1,dr+s-1,s);
    }
    if(dr < tr + s && dc >= tc + s) //在右上角棋盘
        chessboard(tr,tc+s,dr,dc,s);
    else{   //不在右上角棋盘
        board[tr + s - 1][tc + s] = t;
        chessboard(tr,tc+s,tr+s-1,tc+s,s);
    }
    if(dr >= tr + s && dc < tc + s)//左下角
        chessboard(tr+s,tc,dr,dc,s);
    else{
        board[tr + s][tc + s - 1] = t;
        chessboard(tr+s,tc,tr+s,tc+s-1,s);
    }
    if(dr >= tr + s && dc >= tc + s)//右下角
        chessboard(tr+s,tc+s,dr,dc,s);
    else{
        board[tr + s][tc + s] = t;
        chessboard(tr+s,tc+s,tr+s,tc+s,s);
    }
}

每一次分治，都将问题分解为四个规模为原先一半的子问题(边长)，总共需要分解k次。而分解和合并花费的时间为O(1)；因此该算法的时间复杂度为O(4^k)。
(3) 大整数乘法
设有两个二进制数X和Y，现要计算它们的乘积X * Y。按计算规则，X中每个数都要与Y中所有数相乘，因此一般方法下乘法的时间复杂度位O(n²)。
采用分治算法处理降低算法复杂度。将X，Y分别分成两个部分，每个部分分别有n / 2位。大整数乘法
则有如下关系：
分组运算
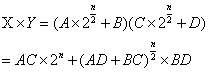
其时间复杂度可以写成如下递归形式：
分治后时间复杂度
对于T(n)，可以计算得到：T(n) = O(n²)，并没有改进算法的性能。
要提升算法性能，需要减少乘法的计算次数。借助如下数学方法，可以提升算法性能。
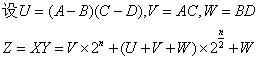
数学方法改进
该计算过程中共进行3次n/2位的乘法运算，6次加减法和2次移位。其时间复杂度：
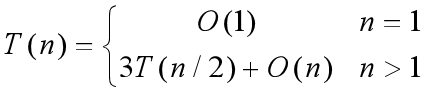
改进后时间复杂度
可计算得T(n) = O(log 3) = O(n^1.59)，算法的性能得到改进。

(4) 矩阵乘法
进行矩阵运算C=A×B，其中A，B为n×n矩阵。矩阵乘法一般的运算方法是：
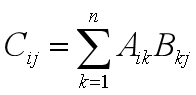
矩阵乘法一般规则
根据该规则，完成一次矩阵乘法，需要进行3次次数为n的循环，因此时间复杂度为O(n³)。
现根据分治策略，将矩阵划分为四个子矩阵。
矩阵分治策略
根据分块矩阵的运算规则，可以得到计算公式：
分治后矩阵乘法运算
其时间复杂度可以写为递归形式：
分治后时间复杂度
可以计算得到，此算法时间复杂度T(n) = O(n³)，未提升算法性能。
为了提升性能，需要减少乘法运算的次数。采用如下数学方法进行优化：
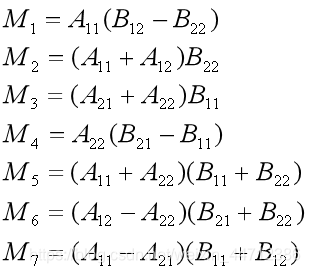
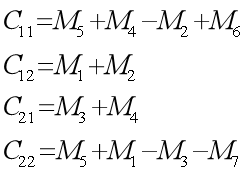
在这里插入图片描述
其时间复杂度的递归形式如下：

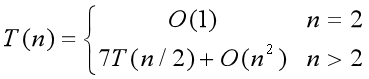
最后算得时间复杂度：T(n) = O(log 7) = O(n^2.87)。