统计学习方法——知识点（2）拉格朗日对偶性

版权声明：署名，允许他人基于本文进行创作，且必须基于与原先许可协议相同的许可协议分发本文 （Creative Commons）

拉格朗日乘数法简介

机器学习的本质是建立模型，使用损失函数对模型的性能进行度量。实现损失函数最小化（优化问题），是一切机器学习的关键。通常对于无约束优化问题，采用梯度下降法、牛顿法/拟牛顿法，对于有约束优化问题，拉格朗日方法应用广泛，是机器学习的理论基础，是理解最优化问题的关键。

拉格朗日方法何时有用？

拉格朗日乘数最常见的应用是找到函数的最大值或最小值（“极值”，即最优化问题），通常会有限制条件。特别是限制变量多且复杂时。如“如何最大限度提升工厂利润，且只有15000元可以投资”。

典型例子：最短路径问题

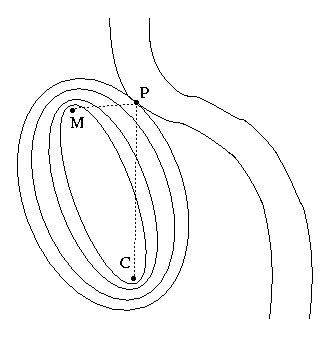
目标函数：求M到C的最短路径；限制条件，需要经过河边。目标函数 $f(x)$可以表述为：以M，C为焦点的椭圆，限制条件是 $g(x,y)=0$的曲线。以M，C为焦点依次从小到大画椭圆，直到椭圆和河岸接触，所得的相切点就是最小路径。

• 在极值点，椭圆（目标函数）与河边曲线（限制条件）相切，具有相同的法线方向。即 $\nabla f(x) = \lambda \nabla g(x)$，其中 $\lambda$是必须的，表示一个比例关系，不改变法线方向。

拉格朗日方法

拉格朗日方法是将求目标函数的条件极值问题转换为拉格朗日函数的无条件极值。
假设 $f(x),c_i(x),h_j(x)$是定义在 $R^n$上的连续可微函数。考虑约束最优化问题（又称凸优化问题）
$\underset{x∈R^n}{min}f(x) \tag 1$s.t. $c_i(x) \leq 0, \quad i=1,2,\cdots,k\tag 2$ $h_j(x)=0, \quad j=1,2,\cdots,l \tag 3$引进广义拉格朗日函数（generalized Lagrange function） $L(x,\alpha,\beta)=f(x)+\sum_{i=1}^k{\alpha_ic_i(x)}+\sum_{j=1}^l\beta_jh_j(x) \tag 4$这里， $\alpha_i,\beta_i$是拉格朗日乘子， $\alpha_i\geq0$，考虑 $x$的函数： $\theta_P(x)=\underset{\alpha,\beta;\alpha_i \geq0}{max}L(x,\alpha,\beta)$注：假设这一函数是关于 $\alpha,\beta$的函数，选择恰当的 $\alpha,\beta$，使目标函数最大化。

未完待续，持续完善

参考：
1、李航《统计学习方法》
2、http://www.slimy.com/~steuard/teaching/tutorials/Lagrange.html