机器学习自学笔记——最好懂的支持向量机

文章目录

文献参考

· 百度知道：桂纶美

基本概念

支持向量

概念：位于分类超平面附近的样本点，称为支持向量

在数学中，点这个概念常常用向量去取代。比如在直角坐标系下，点A坐标为(3,4)，我们可以认为它代表着向量OA = (3,4)

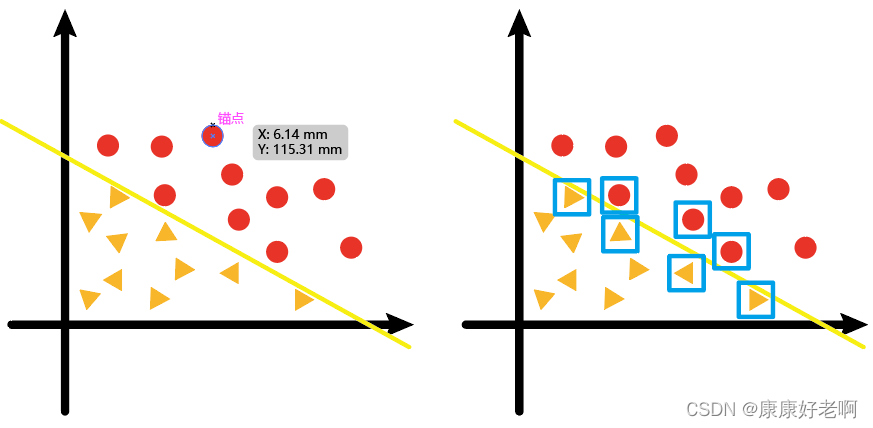
现在我们有如下左图的一个二维样本点（向量），其中黄色的线是经过线性回归计算得出来的分类线；而右图那些临近回归线的点（用蓝色方形标注），就叫做支持向量。

“支持” 的含义可以这样理解：

那些临近分类边界的点，才是对回归线（超平面）的走向有影响的点；距离分类边界较远的点，它们对回归线（超平面）如何去画并没有什么影响

请添加图片描述

如果我们将“机”理解成“算法”，那么支持向量机不难理解为“与支持点相关的(求出分类超平面的)算法”

下面给出支持向量机较为标准的概念：

支持向量机(SVM)

是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器。

对于下面这一些数据集，要用一条回归线将其分开，现有①、②、③三条线，哪一条效果最好呢？

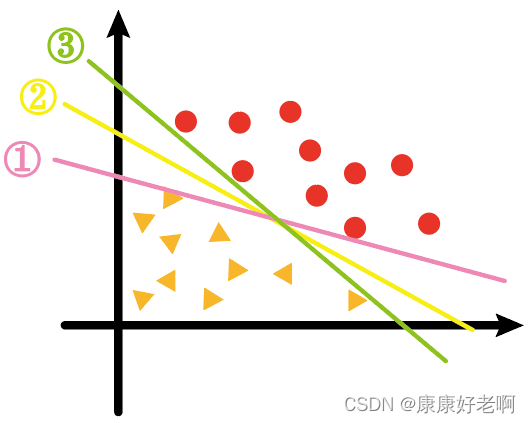
请添加图片描述

我想绝大部分人都会认为是②。虽然三条线都满足了将三角形和圆形分开，但是对于②线来说，三角形和圆形的支持向量到②线的距离看上去更加“均衡”，像是从中间位置将其分隔。

其实，支持向量机的意思是指：求支持向量到超平面的距离之和尽可能的大的算法。

事实上，根据基本不等式，距离之和最大和距离更加“均衡”其实是等价的

那么这里就引出了最大间隔超平面的概念

最大间隔超平面

上图中对应的②线——也就是我们看起来的最“均衡线”，它其实是以最大间隔把两类样本分开的线（高维的称作超平面），即最大间隔超平面。

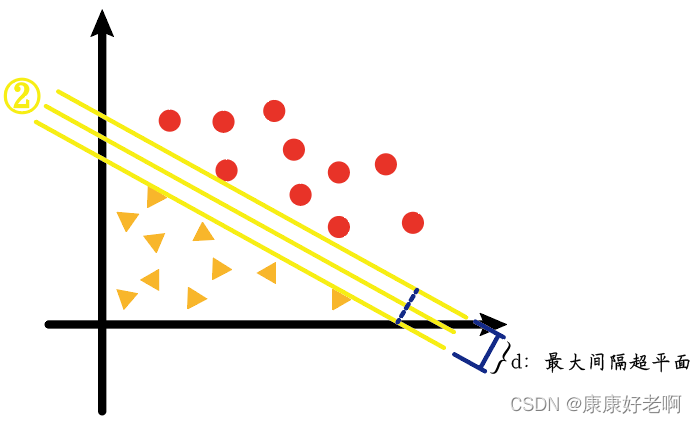
请添加图片描述

我们会发现①、③两条线的样本间隔要比②的小很多，如下图

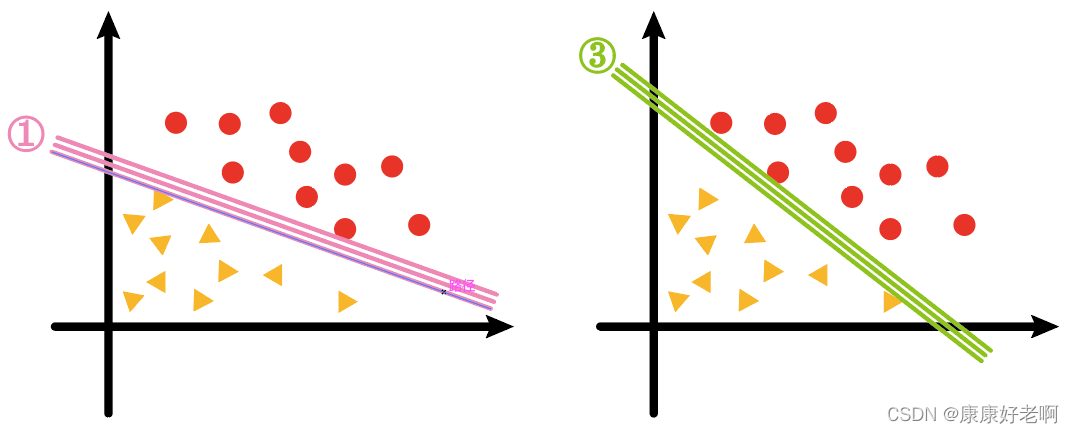
请添加图片描述

而我们支持向量机算法（SVM）实质上求的就是②这样的线、平面或者超平面

软间隔与硬间隔

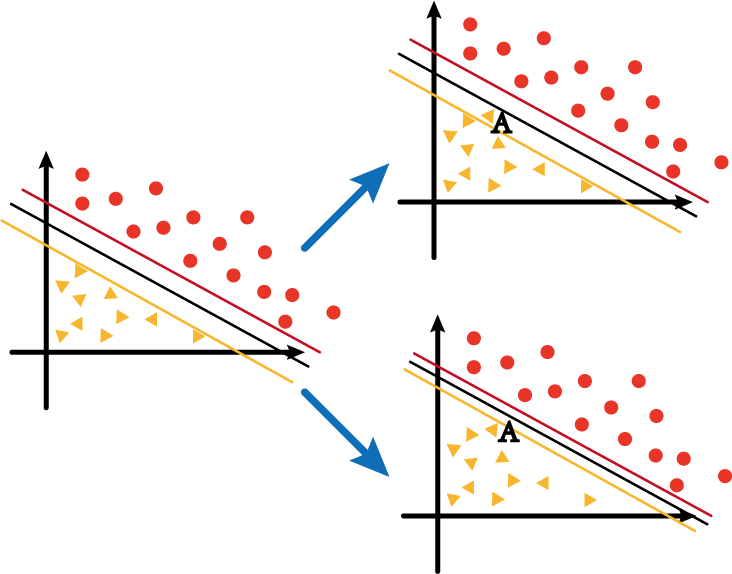
请添加图片描述

假设上图中左边的坐标系中黄色、黑色和红色分别为负/决策/正超平面，而此时如果在黄线和红线之间新增了一个数据点 $A$ ，那么围绕超平面是否进行调整，会分成两种情况：

第一种就是右上角的图1，虽然加入了 $A$ ，但是仍然使其在黄线与红线之间；
第二种就是右下角的图2，随着 $A$ 的加入，超平面也随之发生变化，最终保证 $A$ 在黄线之下。

第一种情况中的黄线与红线的距离我们称之为软间隔；第二种情况中的黄线与红线的距离我们称之为硬间隔。

SVM最优化问题求解思路

在线性代数中，任意超平面可以用下面这个线性方程来描述：
$W^{T}X+b=0$
其中
$W=[w_1,w_2,···，w_n]$

$X=[x_1,x_2,···，x_n]$

为系数矩阵，矩阵W转置后

$\left[ \begin{array} {} W_1\\ W_2\\ ·\\ ·\\ ·\\ W_n \end{array} \right]$

故
$W^TX=w_1x_1+w_2x_2+w_3x_3+···+w_nx_n$
就是我们正常看到的超平面函数表达式

根据点到直线的距离公式

$\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$
从二维拓展成高维
$\frac{|w_1x_1+w_2x_2+w_3x_3+···+w_nx_n+b|}{\sqrt{w_1^2+w_2^2+···+w_n^2}}$
其中
$w_1x_1+w_2x_2+w_3x_3+···+w_nx_n=W^TX$
为前面所得出的公式
$\sqrt{w_1^2+w_2^2+···+w_n^2}=||W||$
为向量的模的定义

对于二维向量 X = (3,4)，其模
$||X||=\sqrt{3^2+4^2}=5$
高维向量以此类推

所以上面的高维距离公式可以转化为

$\frac{|W^TX+b|}{||W||}$

支持向量机数学原理

通过上文介绍，我们大概了解了支持向量机的作用与简单原理。下面我们详细介绍一下支持向量机的数学原理以及其算法。

第一步：建立支持向量方程

首先补充一下上文介绍超平面的内容。我们一般将中间的用于分隔的超平面叫做决策超平面，决策超平面也是我们最后求得的超平面。而决策超平面的正方向与负方向分别有两个超平面：正超平面和负超平面。这两个超平面用于辅助生成决策超平面。为了简单化，我们先只考虑二维的支持向量机。

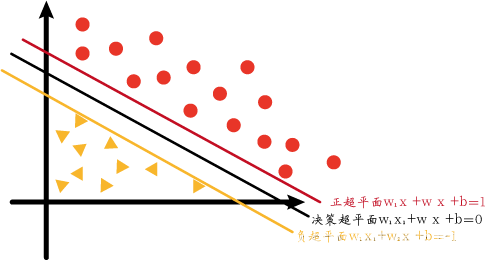
请添加图片描述

图中正超平面、决策超平面、负超平面的方程分别如下：
$w_1x_1+w_2x_2+b=1\\w_1x_1+w_2x_2+b=0\\w_1x_1+w_2x_2+b=-1$
这个并非是超平面的唯一写法。前面基础部分我们介绍了线性方程如何用矩阵来表达，这种写法只是上面的一种等价变式（移项），方便后面的运算。

现在我们假设在正超平面和负超平面上分别有两个支持向量M和N。他们分别满足下式：
$w_1x_{1m}+w_2x_{2m}+b=1\\w_1x_{1n}+w_2x_{2n}+b=-1$
目前现有的这两个方程对我们并没有什么作用或者启发，考虑到两个式子中都可以提出公因子 $w_1、w_2$ ，以及都有常数 $b$ ，所以我们将两式作差，会得到如下结果：
$w_1(x_{1m}-x_{1n})+w_2(x_{2m}-x_{2n})=2$
如果我们将上述式子看成两个向量做点积，我们会得到：
$\vec{w}(\vec{x_m}-\vec{x_n})=2$
其中 $\vec{w}=[w_1 \ w_2]$ ， $\vec{x_m}=[x_{1m} \ x_{2m}]^T$ ， $\vec{x_n}=[x_{1n} \ x_{2n}]^T$

根据 $\vec{a}·\vec{b}=||\vec{a}||*||\vec{b}||*cos\theta$ ，
$||\vec{w}||*||\vec{x_m}-\vec{x_n}||*cos\theta=2$
其中 $||\vec{w}||=\sqrt{w_1^2+w_2^2}$ 。

移项
$||\vec{x_m}-\vec{x_n}||*cos\theta=\frac{2}{||\vec{w}||}$

通过移项 $x$ 与 $w$ 分别在等式左右两边。左边是数据点的坐标，右边是待求的权重值。

第二步：求出最大间隔 $L$ 表达式

这里我们不妨思考下 $||\vec{x_m}-\vec{x_n}||*cos\theta$ 的意义。

所以我们画出下图，尝试从几何角度去观察上式的意义。

我们知道向量点积可以转化为投影，即将一个向量的模乘 $cos\theta$ 投影到另外一个向量的方向上，相同方向会极大的方便计算。

请添加图片描述

于是我们画出了下面的坐标系与向量（称为图1）。我们想用向量点积投影，但是我们并不知道MN和 $\vec{w}$ 的夹角。

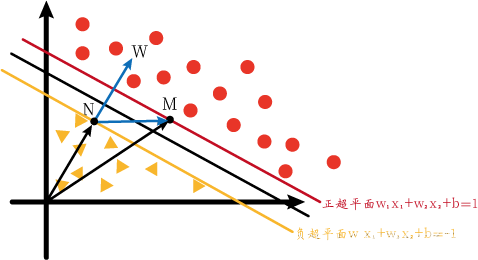
请添加图片描述

但是我们可以进行转化。我们知道M、N两点在正负超平面上，那如果M、N在决策超平面上呢？由于这三个超平面的方程只有等号右边的常数不一样，所以如果M、N在决策超平面上时的 $\vec{w}$ 应该与上图的一样。所以我们不妨先设M、N在决策超平面上。我们可以画出下图（称为图2）：

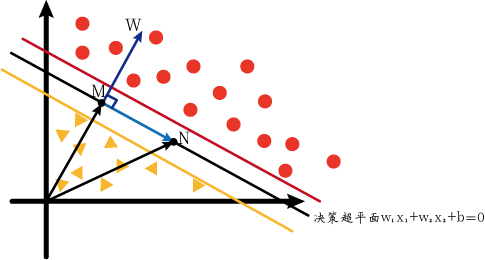
请添加图片描述

此时的M、N分别满足下列式子：
$w_1x_{1m}+w_2x_{2m}+b=0\\w_1x_{1n}+w_2x_{2n}+b=0$
两式作差，可以得到：
$w_1(x_{1m}-x_{1n})+w_2(x_{2m}-x_{2n})=0$
即
$\vec{w}(\vec{x_m}-\vec{x_n})=0$
向量点积为零说明两向量互相垂直。观察上图， $\vec{x_m}-\vec{x_n}$ 即为 $\vec{NM}$ 。而这也就意味着 $\vec{w}$ 垂直于决策超平面，也就垂直与正、负超平面。好，这时我们从图2转回图1，我们再次将图1放出来方便说明。

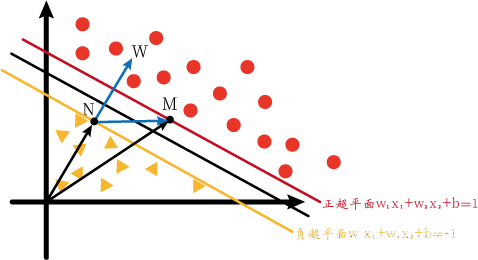
请添加图片描述

由于 $\vec{w}$ 垂直于超平面，所以 $||\vec{NM}||$ 在 $\vec{w}$ 上的投影就为正负超平面的最大间隔 $L$ 。而正好 $||\vec{NM}||=||\vec{x_m}-\vec{x_n}||*cos\theta$ ，故
$L=\frac{2}{||\vec{w}||}$

第三步：求 $L$ 约束条件，得出优化问题

正超平面：所有红点属于正类，所以 $y_i=1$ ；所有红点都在正超平面上方，所以 $\vec{w}·\vec{x_i}+b≥1$

负超平面：所有黄点属于负类，所以 $y_i=-1$ ；所有黄点都在负超平面下方，所以 $\vec{w}·\vec{x_i}+b≤1$

上面两种情况可以总结成下面这个式子：
$y_i*(\vec{w}·\vec{x_i}+b)≥1$
而这个式子就是约束条件。

所以，求决策超平面问题就转化为：

在 $y_i*(\vec{w}·\vec{x_i}+b)≥1$ 条件下， $||\vec{w}||$ 的最小值。

由于 $||\vec{w}||=\sqrt{w_1^2+w_2^2}$ 中含有根号，所以最小值并不是很好求。所以我们转化一下，将 $||\vec{w}||$ 转化成 $\frac{||\vec{w}||^2}{2}$ ，于是问题等价为：

在 $y_i*(\vec{w}·\vec{x_i}+b)≥1$ 条件下， $\frac{||\vec{w}||^2}{2}$ 的最小值。

第四步：解出优化问题解的前四个条件

这种问题我们会通过拉格朗日乘子法进行求解。

但是有一个问题，就是约束条件 $y_i*(\vec{w}·\vec{x_i}+b)≥1$ 是不等式而不是等式，所以我们要先经过一步转化，将不等式转化为等式。

我们将 $y_i*(\vec{w}·\vec{x_i}+b)≥1$ 转换成 $y_i*(\vec{w}·\vec{x_i}+b)-1=p_i^2$ ，由于 $p_i^2≥0$ 恒成立，故 $y_i*(\vec{w}·\vec{x_i}+b)-1≥0$ 恒成立。

所以原问题等价为：

在 $y_i*(\vec{w}·\vec{x_i}+b)-1=p_i^2$ 条件下， $\frac{||\vec{w}||^2}{2}$ 的最小值。

下面构造拉格朗日函数：
$L(w,b,\lambda_i,p_i)=\frac{||\vec{w}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2)$
然后进行求解。拉格朗日函数对每个未知数求偏导并令其等于0。
$\frac{\partial{L}}{\partial{w}}=0;\frac{\partial{L}}{\partial{b}}=0;\frac{\partial{L}}{\partial{\lambda_i}}=0;\frac{\partial{L}}{\partial{p_i}}=0$
下面我们一个个来计算。

首先是 $\frac{\partial{L}}{\partial{w}}=0$ 。 $w$ 出现在两个位置，分别是 $\frac{||\vec{w}||^2}{2}$ 和 $\sum_{i=1}^s\lambda_i*y_i*(\vec{w}·\vec{x_i}+b)$ ，很容易求导得下式：

$\vec{w}-\sum_{i=1}^s\lambda_iy_i\vec{x_i}=0············①$

然后是 $\frac{\partial{L}}{\partial{b}}=0$ 。 $b$ 只出现在一个位置，为 $\sum_{i=1}^s\lambda_i*y_i*b$ ，很容易求导得下式：

$\sum_{i=1}^s\lambda_iy_i=0············②$

接着是 $\frac{\partial{L}}{\partial{\lambda_i}}=0$ 。 $\lambda_i$ 只出现在一个位置，为 $\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2)$ 。本来求偏导得到的结果应该是 $\sum_{i=1}^{s}{y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2=0}$ ，但其实根据限制条件， $y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2=0$ ，没有必要使用求和符号。

$y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2=0············③$

最后是 $\frac{\partial{L}}{\partial{p_i}}=0$ 。 $p_i$ 只出现在一个位置，为 $\sum_{i=1}^s\lambda_i*(-p_i^2)$ ，很容易求导得到下式：

$2\lambda_ip_i=0············④$

下面的步骤就是利用①~④式和原式求出 $||\vec{w}||$ 的最小值。首先我们将④式左右两边同时除以2并乘 $p_i$ ，得到下式：
$\lambda_ip_i^2=0$
之所以要这样做是因为③式中有一个 $p_i^2$ ，这样做可以一定程度上化简计算。我们将③式代入④式，得到：
$\lambda_i(y_i*(\vec{w}·\vec{x_i}+b)-1)=0$
这个式子非常有趣。之前我们在第三步得到 $y_i*(\vec{w}·\vec{x_i}+b)≥1$ 这个约束条件，那这样上式只可能在两种情况下成立：

① $y_i*(\vec{w}·\vec{x_i}+b)-1)＞0$ ， $\lambda_i=0$ ;

② $y_i*(\vec{w}·\vec{x_i}+b)-1=0$ ， $\lambda_i≠0$ 。

第五步：得出优化问题解的第五个条件

对于拉格朗日函数 $L(w,b,\lambda_i,p_i)=\frac{||\vec{w}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2)$ 来说，当不满足约束条件时，即 $y_i*(\vec{w}·\vec{x_i}+b)-1<0$ 时，如果 $\lambda_i<0$ ，则 $\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2)>0$ ，而 $L(w,b,\lambda_i,p_i)$ 也会更小。根据拉格朗日函数的性质，越符合约束条件拉格朗日函数的值越小。这就说明， $\lambda_i$ 小于0是不符合常理的，故其应该大于等于0。

我们同样也可以通过图像来解释这个问题。

我们假设是二维空间，在这个二维空间中，横纵坐标分别是 $w_1$ 和 $w_2$ ，那么 $||\vec{w}||=\sqrt{w_1^2+w_2^2}$ 在图像上表示的几何含义为一个圆心为原点，半径为 $\sqrt{w_1^2+w_2^2}$ 的圆。

请添加图片描述

我们所要求得的优化问题 $min\frac{||\vec{w}||^2}{2}$ ，即为 $||\vec{w}||$ 取最小值时取到。而由于 $||\vec{w}||$ 即为圆的半径，所以我们希望圆尽可能的小。

现在我们加入约束条件。第一个约束条件为 $g_1=y_1*(\vec{w}·\vec{x_1}+b)-1≥0$ ，它在图像上表示的含义是可行区域在一条直线之上（浅绿色），如下图：

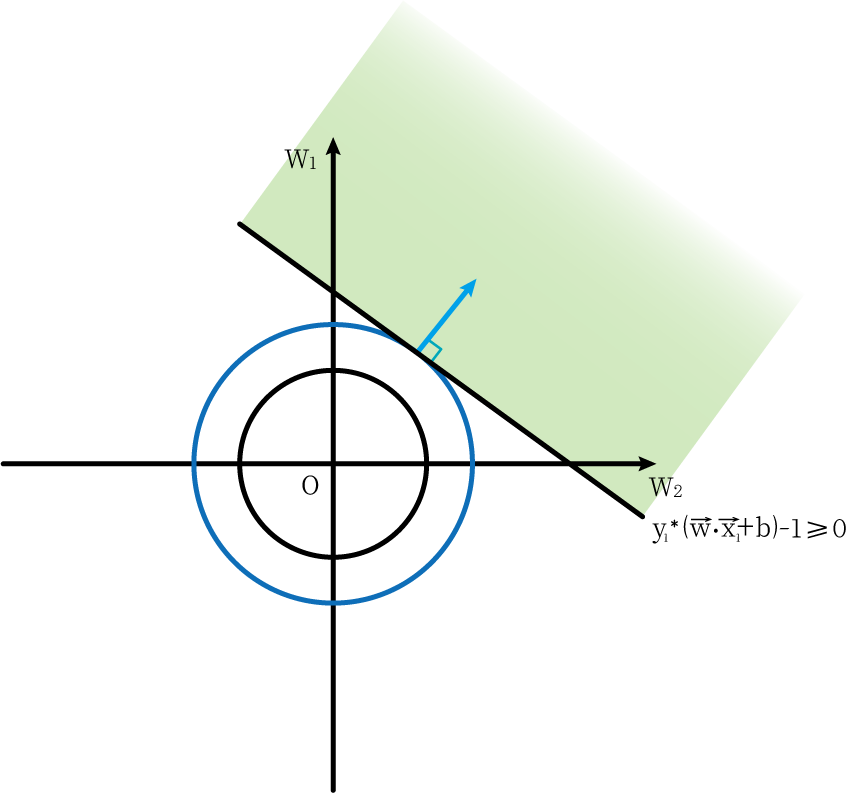
请添加图片描述

而能够使圆上有点能在可行区域之内，且圆的半径要最小的情况就是圆与直线相切（如图中深蓝色圆所表示）

此时我们加入另外一个限制条件， $g_2=y_2*(\vec{w}·\vec{x_2}+b)-1≥0$ 。此时在两个限制条件下，最小的圆是经过两条直线交点的圆。而此时的 $\vec{w}=(w_1,w_2)$ 的方向（红色线所表示）只要在两个直线之内即可。

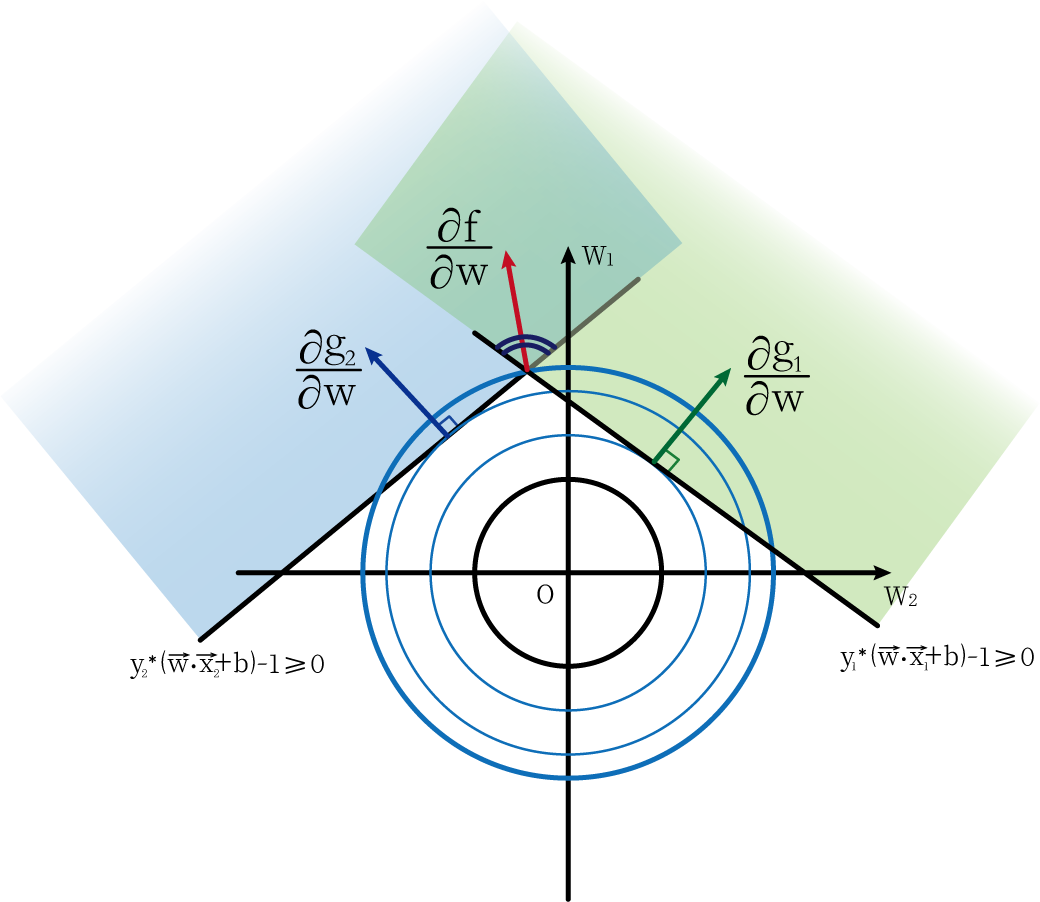
请添加图片描述

通过上图直观理解，我们也可以得出下面一个式子：向量 $\frac{\partial{f}}{\partial{w}}$ 可以由 $\frac{\partial{g_1}}{\partial{w}}和\frac{\partial{g_2}}{\partial{w}}$ 线性表出，而它们的系数 $\lambda_1$ 和 $\lambda_2$ 都为非负数（通过直观理解或者用矢量三角形理解）。
$\frac{\partial{f}}{\partial{w}}=\lambda_1\frac{\partial{g_1}}{\partial{w}}+\lambda_2\frac{\partial{g_2}}{\partial{w}}$
通过上述图像也可以帮助我们理解， $\lambda_i$ 为什么大于等于0。我们也就得到了第五个条件：
$\lambda_i≥0············⑤$
综合上述，我们已经得到了解的五个条件，又称为KKT条件：
$\vec{w}-\sum_{i=1}^s\lambda_iy_i\vec{x_i}=0····················①\\\sum_{i=1}^s\lambda_iy_i=0·························②\\y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2=0············③\\2\lambda_ip_i=0····························④\\\lambda_i≥0·······························⑤$

第六步：转化成SVM对偶问题

对偶问题是一种求解线性规划问题的常用方法。通过将一个问题转化为其对偶问题，有时能大大简化求解问题的难度。

我们先回顾一下原问题：

在 $g_i(w,b)=y_i*(\vec{w}·\vec{x_i}+b)-1=p_i^2$ 条件下， $求\frac{||\vec{w}||^2}{2}$ 的最小值。

我们先假设原问题的最优解为 $w^*、b^*$ 。然后设
$q(\lambda_i)=min(L(w,b,\lambda_i))=min(\frac{||\vec{w}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2))$
代入 $w^*、b^*$ ，可以得到下面的式子：
$q(\lambda_i)=min(L(w,b,\lambda_i))≤min(L(w^*,b^*,\lambda_i))$
即 $min(\frac{||\vec{w}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w}·\vec{x_i}+b)-1-p_i^2))≤\frac{||\vec{w^*}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w^*}·\vec{x_i}+b^*)-1-p_i^2)$

小于等于号的存在是由 $min$ 最小值函数决定的。

根据KKT条件的③和⑤， $\sum_{i=1}^s\lambda_i*(y_i*(\vec{w^*}·\vec{x_i}+b^*)-1-p_i^2)$ 必定大于0，故
$\frac{||\vec{w^*}||^2}{2}-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w^*}·\vec{x_i}+b^*)-1-p_i^2)≤\frac{||\vec{w^*}||^2}{2}$
又由于 $\vec{w^*}$ 是原问题最优解，所以我们可以得到：
$\frac{||\vec{w^*}||^2}{2}≤\frac{||\vec{w}||^2}{2}$
所以我们可以得到下面一个不等式链：
$q(\lambda_i)≤min(L(w^*,b^*,\lambda_i))≤\frac{||\vec{w^*}||^2}{2}≤\frac{||\vec{w}||^2}{2}$
我们假设 $\lambda_i^*为q(\lambda_i)$ 的最优解。则
$q(\lambda_i)≤q(\lambda_i^*)≤\frac{||\vec{w^*}||^2}{2}≤\frac{||\vec{w}||^2}{2}$
好，进行到这一步我们就可以将原问题转化成对偶问题了。

原问题：

在 $g_i(w,b)=y_i*(\vec{w}·\vec{x_i}+b)-1≥0$ 条件下， $求\frac{||\vec{w}||^2}{2}$ 的最小值。

对偶问题：

在 $\lambda_i≥0$ 的条件下，求 $q(\lambda_i)=min(L(w,b,\lambda_i))$ 的最大值。

当 $q(\lambda_i^*)=\frac{||\vec{w^*}||^2}{2}$ 时，两个问题为强对偶问题，应同时取得最优解，下面进行证明：

因为
$q(\lambda_i)≤\frac{||\vec{w}||^2}{2}$
所以
$q(\lambda_i^*)≤\frac{||\vec{w}||^2}{2}$
故
$\frac{||\vec{w^*}||^2}{2}≤\frac{||\vec{w}||^2}{2}$
而又根据前面得到的 $q(\lambda_i)≤min(L(w^*,b^*,\lambda_i))≤\frac{||\vec{w^*}||^2}{2}$ ，所以
$q(\lambda_i)≤\frac{||\vec{w^*}||^2}{2}=q(\lambda_i^*)$
所以 $q(\lambda_i^*)$ 为 $q(\lambda_i)$ 的最大值解。

故证明在强对偶条件下，原问题和对偶问题的最优解同时取到。

第七步：优化方程

根据前面的拉格朗日函数，我们已经得到：
$max(q(\lambda))=max(min(\frac{||\vec{w}||}{2})-\sum_{i=1}^s\lambda_i*(y_i*(\vec{w^*}·\vec{x_i}+b^*)-1)))$
将KKT条件代入化简可得：
$max(q(\lambda))=max(\sum_{i=1}^s{\lambda_i}-\frac{1}{2}\sum_{i=1}^{s}\sum_{j=1}^s\lambda_i\lambda_jy_iy_j\vec{x_i}·\vec{x_j})$

第八步：得出算法步骤

上文我们推导过下列式子：

① $y_i*(\vec{w}·\vec{x_i}+b)-1>0$ ， $\lambda_i=0$ ;

② $y_i*(\vec{w}·\vec{x_i}+b)-1=0$ ， $\lambda_i≠0$ 。

同时我们也推导出 $\lambda_i≥0$ 这个条件。

根据上面的两个条件我们可以得到一些结论。

如果数据点在正负超平面 $\vec{w}·\vec{x_i}+b±1=0$ 上，由于 $y_i|=1$ ，所以 $y_i*(\vec{w}·\vec{x_i}+b)-1=0$ ，则属于情况②，故 $\lambda_i＞0$ 。
如果数据点不在正负超平面上 $\vec{w}·\vec{x_i}+b±1=0$ 上，则属于情况①，所以 $\lambda_i=0$ 。而将 $\lambda_i=0$ 代入可得 $\lambda_i(y_i*(\vec{w}·\vec{x_i}+b)-1)=0$ 。

上述推导说明，我们在计算超平面权重值 $w$ 时只需要用到支持向量（在正负超平面上的数据点），而不需要非支持向量。

有了前文铺垫，我们就可以得出支持向量机SVM算法了。

① 通过下列问题求得 $\lambda_i$ 的值
$max(q(\lambda))=max(\sum_{i=1}^s{\lambda_i}-\frac{1}{2}\sum_{i=1}^{s}\sum_{j=1}^s\lambda_i\lambda_jy_iy_j\vec{x_i}·\vec{x_j})\\其中\lambda_i≥0$
② 根据KKT条件
$\vec{w}=\sum_{i=1}^s\lambda_iy_i\vec{x_i}$
可以求出 $\vec{w}$

标题

③ 根据 $y_i*(\vec{w}·\vec{x_i}+b)-1=0$ 求解出 $b$

升维转换与核技巧

我们看下面一个情景：

比如现在在一维x轴上有一些数据点，红色和蓝色。我们现在想要将其用一个函数（对于一维来说就是一个常量）去划分红点和蓝点。很直观地可以看出，这个是不可能的。

请添加图片描述

但是，如果上图是由二维平面图形投影到一维x轴上而产生的，我们“还原”二维平面，或许会发现不一样的世界：

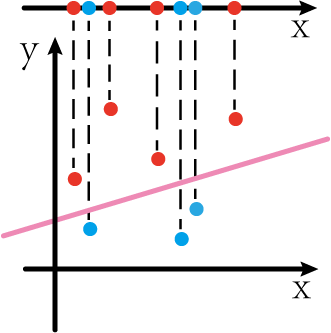
请添加图片描述

如上图，如果我们能通过某些方法将一维的数据点转化为二维的数据点，那么我们似乎可以很容易对数据点进行划分（如图中粉红色那条线）

这一过程即为升维转换。

在支持向量机中我们也可以利用这个方法。我们先回顾下优化方程：
$max(q(\lambda_i))=max(\sum_{i=1}^s{\lambda_i}-\frac{1}{2}\sum_{i=1}^{s}\sum_{j=1}^s\lambda_i\lambda_jy_iy_j\vec{x_i}·\vec{x_j})\\其中\lambda_i≥0$
$\vec{x_i}·\vec{x_j}$ 表示在原维度下对应向量坐标的点积。但是事实上，上述方程是无解的，所以我们可以利用核技巧进行升维变换。我们会通过一个函数 $T (x)$ 进行升维变换操作，这个函数我们称之为维度转换函数。通过维度转换函数，原来的 $\vec{x_i}$ 变成了 $T(\vec{x_i})$ ， $\vec{x_j}$ 变成了 $T(\vec{x_j})$ 。所以原问题也转换成了下式：
$max(q(\lambda_i))=max(\sum_{i=1}^s{\lambda_i}-\frac{1}{2}\sum_{i=1}^{s}\sum_{j=1}^s\lambda_i\lambda_jy_iy_jT(\vec{x_i})·T(\vec{x_j}))\\其中\lambda_i≥0$
事实上，这里我们既可以通过 $\vec{x_i}、\vec{x_j}$ 写出 $T(\vec{x_i})、T(\vec{x_j})$ ，然后再进行点积操作，也可以直接令 $K(\vec{x_i},\vec{x_j})=T(\vec{x_i})·T(\vec{x_j})$ ，然后进行计算。这两者的区别在于，后者是直接将 $\vec{x_i}·\vec{x_j}$ 看成一个未知数整体代入计算。而这里的 $K(\vec{x_i},\vec{x_j})$ 即为核函数。其一般表达式如下：
$K(\vec{x_i},\vec{x_j})=(c+\vec{x_i}·\vec{x_j})^d$
那么参数 $c 和 d$ 都有什么作用呢？

对于相同的 $d$ ，不同的 $c$ 来说， $c$ 可以控制低次项的存在与否，以及低次项的系数；

对于相同的 $c$ ，不同的 $d$ 来说， $d$ 的大小决定了最高维度大小。

除此之外，核函数还可以由多个核函数线性组合而成，比如： $K_1'(\vec{x_i},\vec{x_j})+K_2'(\vec{x_i},\vec{x_j})$

也有一种比较特殊的核函数，即将二维转化成无穷维。这个核函数是高斯核函数(RBF)，其公式如下：
$K(\vec{x_i},\vec{x_j})=e^{-\gamma||\vec{x_i}-\vec{x_j}||^2}$

软间隔

前文中解释过软硬间隔的概念，下面我们详细讨论下。

请添加图片描述

如上图，有个点A违反了约束条件，在黄线和黑线之内。

我们知道硬间隔约束条件为 $y_i*(\vec{w^*}·\vec{x_i}+b^*)-1≥0$ 。如果点A违背约束条件，则点A满足式子 $y_a*(\vec{w^*}·\vec{x_a}+b^*)-1＜0$ 。我们想要把不等式转化为等式，则需要一个 $\epsilon_a$ 来衡量误差，式子如下：
$\epsilon_a=1-y_a*(\vec{w^*}·\vec{x_a}+b^*)$
所以软间隔优化问题如下：

在 $g_i(w,b)=y_i*(\vec{w}·\vec{x_i}+b)-1＞0$ 和 $max(0,1-y_a*(\vec{w^*}·\vec{x_a}+b^*))$ 条件下，

$求\frac{||\vec{w}||^2}{2}+C\sum_{i=1}^s{\epsilon_i}$ 的最小值。

我们可以和之前的硬间隔优化问题进行比对：

在 $g_i(w,b)=y_i*(\vec{w}·\vec{x_i}+b)-1＞0$ 条件下，

$求\frac{||\vec{w}||^2}{2}$ 的最小值。

事实上，软间隔相比于硬间隔的最大差别是在于多了一项
$C\sum_{i=1}^s{\epsilon_i}$
这一项的意思就是，将所有的误差 $\sum_{i=1}^s{\epsilon_i}$ 考虑到优化问题中，这样求最小值的时候也能够起到减少误差的作用。而常数 $C$ 是我们人为规定的，它起到调节误差容忍度的作用。

$C$ 越大，说明对 $\epsilon_i$ 的容忍度越小，也就是最终算出来的结果中产生的误差越少；
$C$ 越小，说明对 $\epsilon_i$ 的容忍度越大，也就是最终算出来的结果中产生的误差越大；