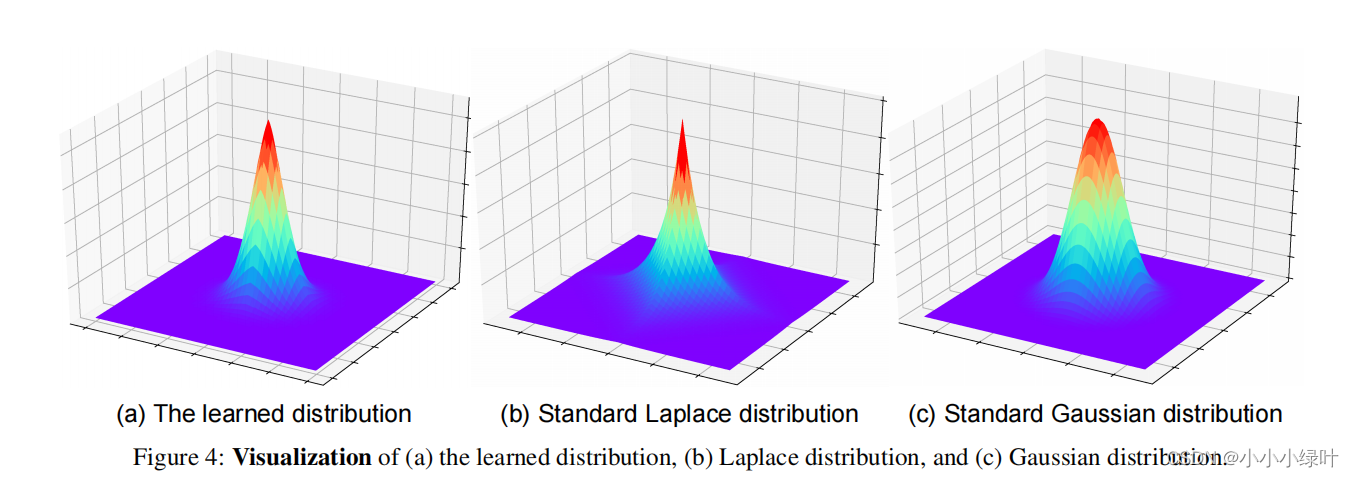
最近看了一篇论文Human Pose Regression with Residual Log-likelihood Estimation(RLE)很有意思,而且效果贼棒,与大家分享一下。
前言
做过关键点的同学都知道,一般Heatmap-based方法在性能上会优于Regression-based的方法。因为Heatmap-based方法通过显式地渲染高斯热图,让模型学习输出的目标分布,将输入图片滤波成为最终希望得到的高斯热图即可,这极大地简化了模型的学习难度,并且这种方式规定了学习的分布,相对于除了结果以外内部一切都是黑盒的Regression-based方法,对于各种情况(遮挡、动态模糊、截断等)要鲁棒得多。
但是,相较于Heatmap-based方法,Regression-based也有其无法比拟的地方。Regression-based方法不需要生成heatmap,计算成本内存开销较低。同时,Regression-based方法输出是连续的,不必担心量化误差。那么Heatmap为什么性能会由于Regression呢?
总结来说,Heatmap全卷积的结构能够完整地保留位置信息,因此高斯热图的空间泛化能力更强。而回归方法因为最后需要将图片向量展开成一维向量,reshape过程中会对位置信息有所丢失。除此之外,Regression中的全连接网络需要将位置信息转化为坐标值,对于这种隐晦的信息转化过程,其非线性是极强的,因此不好训练和收敛。
动机
论文发现在Regression-based方法中,使用L1 loss效果优于L2 loss。从极大似然估计的角度来理解,L1 loss服从拉普拉斯的先验假设,而L2 loss则服从高斯分布先验假设,一个合适的概率分布对于回归是有益的。RLE可以帮助网络构建误差概率分布的损失,模拟生成真实误差概率分布,相较于heatmap显示地将分布标注并作为学习目标,RLE隐性的概率分布损失可以帮助regression更好的回归。
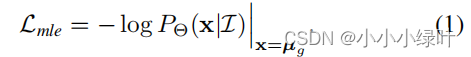
我们解释一下如何从极大似然估计的角度去理解L2, L1损失。看到公式1, P Θ ( X ∣ I ) P_\Theta{(X|\mathcal{I})} PΘ(X∣I),表示GT出现在位置x中的概率,其中Θ表示可学习的模型参数, μ g \mu_g μg表示GT坐标。 L m l e L_{mle} Lmle就是它的似然函数。假设概率密度函数是高斯分布,那么模型需要预测两个值 μ ^ , σ ^ \hat{\mu},\hat{\sigma} μ^,σ^来构建 P Θ ( X ∣ I ) P_\Theta{(X|\mathcal{I})} PΘ(X∣I)。
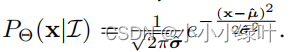
当我们最大化它的似然函数,那么损失函数就可以看作公式2。如果,我们把公式2中的 σ ^ \hat{\sigma} σ^看作常数,损失就退化成标准的L2 loss: L = ( μ g − μ ^ ) 2 L=(\mu_g-\hat{\mu})^2 L=(μg−μ^)2.同理,当假设概率密度函数是拉普拉斯分布时,损失退化成标准的L1 loss。
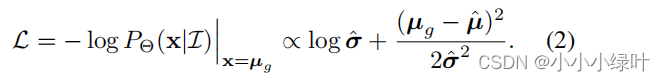
RLE为了获得合适的概率分布,使用Flow-based generative model去模拟并生成误差概率分布。
Flow-based generative model
论文使用Flow-based方法生成误差概率分布,想详细了解Flow-based generative model的请参考这里。下面我简单介绍一下这部分内容。
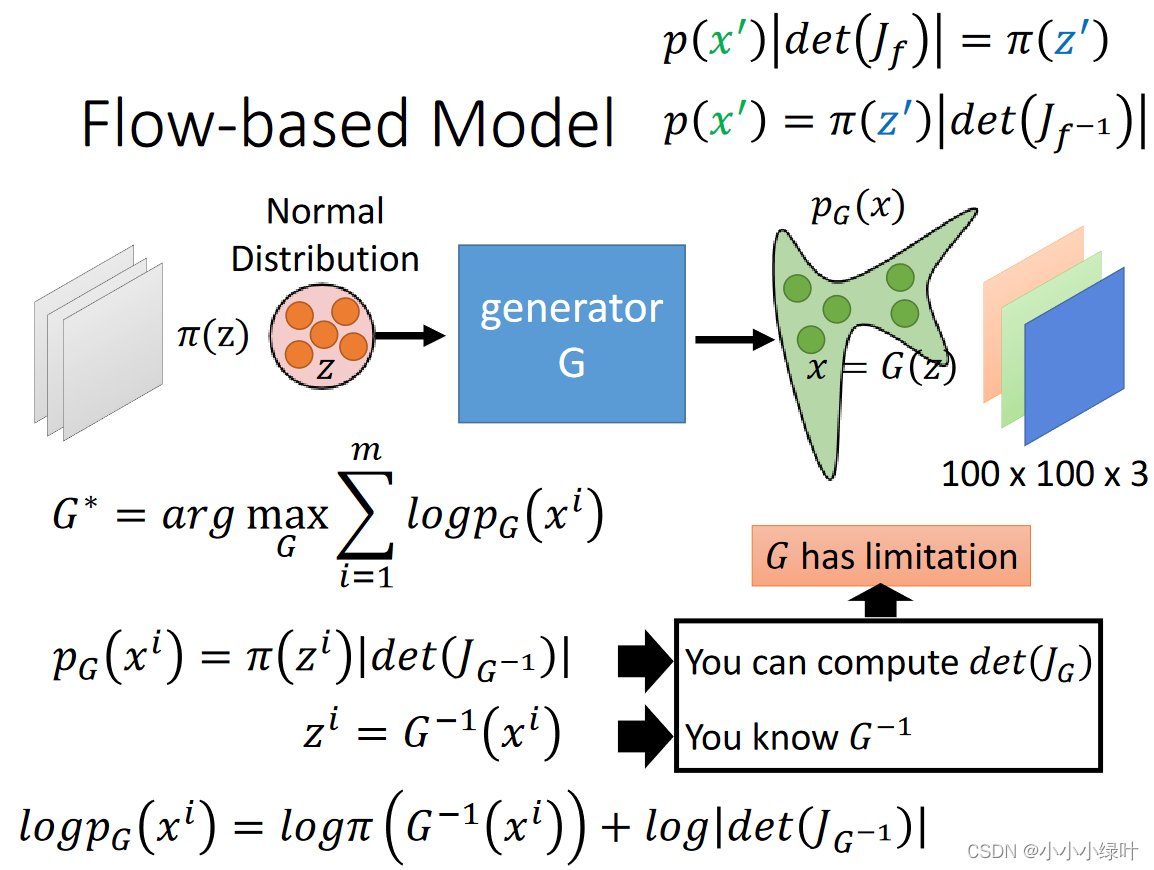
假设我们已知两个概率密度函数 π ( z ) , p ( x ) \pi(z),p(x) π(z),p(x),这两个概率密度函数存在 x = f ( z ) x=f(z) x=f(z)这样的映射关系。由于存在映射关系,所以两个函数对应部分积分的面积是相等的,我们可以获得 p ( x ) ∣ d e t ( J f ) ∣ = π ( z ) p(x)|det(J_f)|=\pi(z) p(x)∣det(Jf)∣=π(z)等式,这个等式是Flow论文中推理出来的,我们可以默认他是对的。下图中的 P G P_G PG就是一个随机参数的概率密度函数,我们从 P d a t a P_{data} Pdata真实样本分布中抽取样本 x i x^i xi,将其带入 P G ( x i ) P_G(x^i) PG(xi),并max( l o g P G ( x i ) logP_G(x^i) logPG(xi)),通过极大似然损失不断迭代就可以使 P G P_G PG越来越接近 P d a t a P_{data} Pdata。Flow中通过CNN来定义映射函数f,也就是生成器G。
事实上在RLE中,RLE通过流模型的极大似然损失训练生成器G,并通过G去修正基础分布(高斯分布或者拉普拉斯分布)。
Design
下面介绍论文是如何设计Flow-based model,获取生成器的极大似然损失,从而生成真实误差概率分布,提高Regression-based精度。
1.Basic Design
假设基础分布 P Θ ( Z ∣ I ) P_\Theta(Z|I) PΘ(Z∣I)服从高斯分布,样本 μ , σ \mu,\sigma μ,σ来自regression的predict(这里会多预测2个方差,作为 σ \sigma σ),同时 X = f ϕ ( z ) X=f_\phi(z) X=fϕ(z),其中 ϕ \phi ϕ是flow model的可学习参数。那么 P Θ P_\Theta PΘ如公式3所示。
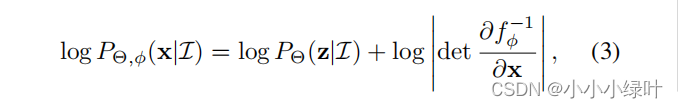
直接学习关键点真实坐标 μ g \mu_g μg的样本分布,训练时从真实样本即GT: μ g \mu_g μg中抽样,通过最大化 L m l e L_{mle} Lmle,将 P Θ , P d a t a P_\Theta,P_{data} PΘ,Pdata拉近。但是这样设计对于流模型的训练不太友好,因为每次输入的样本 ( μ , σ ) (\mu,\sigma) (μ,σ)不同,训练样本分散,模型拟合过于困难。
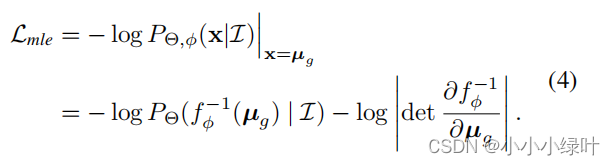

公式4中的loss会引导 ϕ \phi ϕ学习拟合所有图像中µg的分布。为了更好的训练流模型,RLE选择对 ( μ , σ ) (\mu,\sigma) (μ,σ)重参数化学习生成误差概率分布。
2.Reparameterization
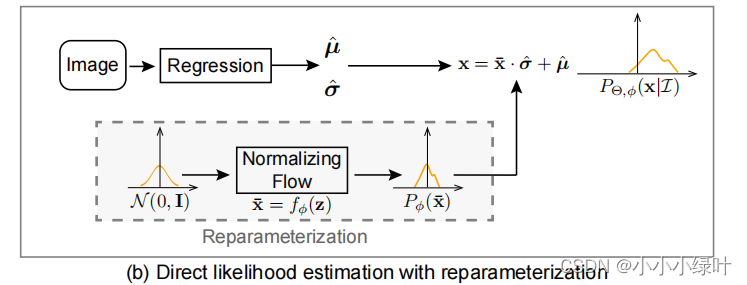
如图b所示,RLE学习误差概率分布,用重参数化技巧将 ( μ , σ ) (\mu,\sigma) (μ,σ)重参成误差 μ ˉ g = ( μ g − μ ^ ) / σ ^ \bar{\mu}_g=(\mu_g-\hat{\mu})/\hat{\sigma} μˉg=(μg−μ^)/σ^。基础分布 π ( z ˉ ) \pi(\bar{z}) π(zˉ)设置为标准正态分布, X ˉ = f ϕ ( z ) \bar{X}=f_\phi(z) Xˉ=fϕ(z). L m l e L_{mle} Lmle如下所示,当回归模型趋于稳定时,回归预测的 μ ^ \hat{\mu} μ^会逐渐接近target μ ˉ \bar{\mu} μˉ,流模型的输入样本 μ ˉ g = ( μ g − μ ^ ) / σ ^ \bar{\mu}_g=(\mu_g-\hat{\mu})/\hat{\sigma} μˉg=(μg−μ^)/σ^也会趋向于0,简化了流模型的收敛难度。
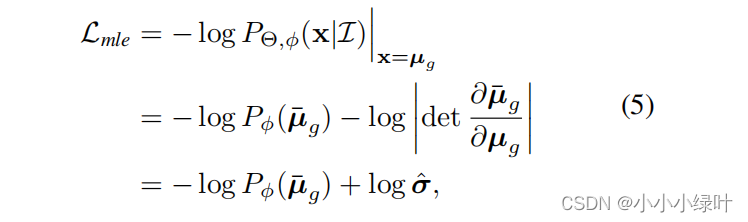
由于训练过程中regression预测的 μ ^ , σ ^ \hat{\mu},\hat{\sigma} μ^,σ^与 f ϕ f_\phi fϕ是耦合的,在训练的开始阶段,坐标预测误差很大、Flow也刚开始训练,很可能Flow学到了错误的误差分布,而 Regressor 又采用了这种错误的误差分布(损失函数)作为指导,无法互相促进。这增加了训练回归模型的难度,并可能会降低模型的性能。
3.Residual Log-likelihood Estimation.
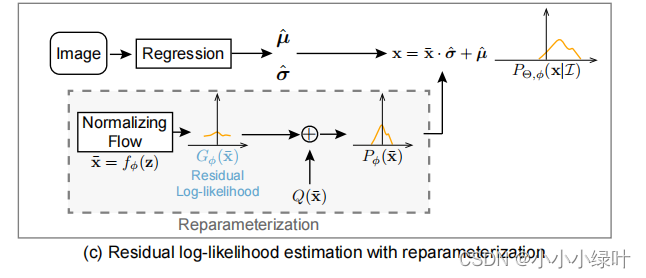
为了便于训练,RLE设计了残差对数似然结构来减少这两个模型之间的依赖性。
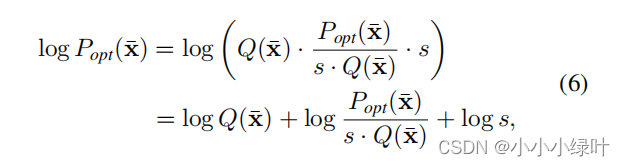
形式上,流模型预测的分布 P ϕ ( X ˉ ) P_\phi(\bar{X}) Pϕ(Xˉ)试图拟合最优的潜在分布 P o p t ( X ˉ ) P_{opt}(\bar{X}) Popt(Xˉ),如公式6被分成3部分,其中 Q ( X ˉ ) Q(\bar{X}) Q(Xˉ)服从(0,1)正态分布, l o g P o p t ( X ˉ ) s ∗ Q ( X ˉ ) log\frac{P_{opt}(\bar{X})}{s*Q(\bar{X})} logs∗Q(Xˉ)Popt(Xˉ)是论文提出的残差对数似然结构,s是为了确保残差对数似然结构满足概率密度函数的要求而设置的常数。如公式14所示,因为 P ϕ ( X ˉ ) P_\phi(\bar{X}) Pϕ(Xˉ)是概率密度函数,对x积分的值为1,所以s可以设置为常数,该值对损失没有影响。
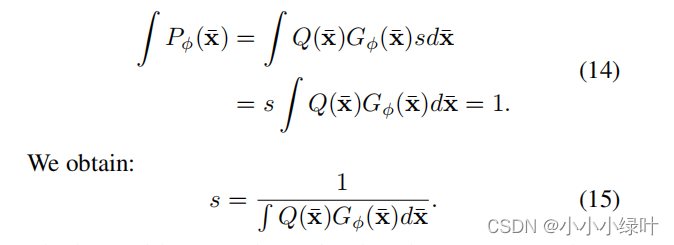
因为误差 μ ˉ g = ( μ g − μ ^ ) / σ ^ \bar{\mu}_g=(\mu_g-\hat{\mu})/\hat{\sigma} μˉg=(μg−μ^)/σ^符合中心极限定理,RLE假设 Q ( X ˉ ) Q(\bar{X}) Q(Xˉ)大概匹配误差潜在分布, l o g P o p t ( X ˉ ) s ∗ Q ( X ˉ ) log\frac{P_{opt}(\bar{X})}{s*Q(\bar{X})} logs∗Q(Xˉ)Popt(Xˉ)可以在 Q ( X ˉ ) Q(\bar{X}) Q(Xˉ)的基础上做出合理的调整,生成合适的误差概率分布。最终的loss如公式8所示。
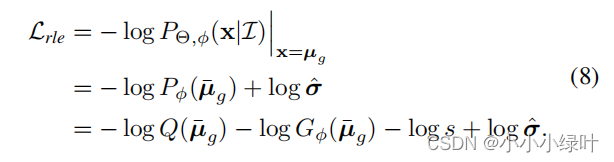
Conclusion
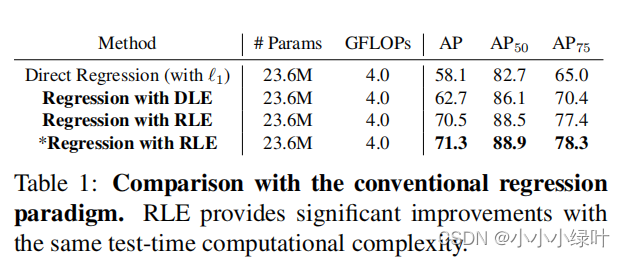
从结果来看,RLE通过无监督极大似然损失,帮助模型感知误差概率分布,与L1 Regression方法相比,提高了AP 12.4%。RLE多引入了方差,在RLE方法中,模型预测的sigma是完全自适应优化的,用来反映模型预测的不确定度。 σ \sigma σ为何可以在没有target的情况下获得模型预测均值的不确定性呢?
σ \sigma σ最开始时是模型预测出来的随机值,随着回归损失梯度下降,预测的 μ ^ \hat\mu μ^会越来越接近target μ g \mu_g μg。由于误差 μ ˉ g = ( μ g − μ ^ ) / σ ^ \bar{\mu}_g=(\mu_g-\hat{\mu})/\hat{\sigma} μˉg=(μg−μ^)/σ^服从流模型生成的误差概率分布(此分布在基础分布(0,1)正态分布上做出修正),因此 μ ˉ g \bar\mu_g μˉg应趋于0。而RLE loss中存在 l o g σ log\sigma logσ,随着梯度下降 σ \sigma σ也会趋近于0。当输入样本图片的关键点语义清晰没有遮挡时,误差 μ ˉ g = ( μ g − μ ^ ) / σ ^ \bar{\mu}_g=(\mu_g-\hat{\mu})/\hat{\sigma} μˉg=(μg−μ^)/σ^的分子更容易趋于0,因此 σ ^ \hat\sigma σ^趋于0的裕量较大。然而,当输入关键点存在遮挡时,预测的 μ ^ \hat\mu μ^与target μ g \mu_g μg容易产生误差,误差 μ ˉ g = ( μ g − μ ^ ) / σ ^ \bar{\mu}_g=(\mu_g-\hat{\mu})/\hat{\sigma} μˉg=(μg−μ^)/σ^的分子不易趋于0,误差 μ ˉ g \bar{\mu}_g μˉg又需要服从流模型的误差概率分布,因此 σ ^ \hat\sigma σ^趋于0的裕量较小。
总结来说,关键点图片质量越高,预测出来的 σ ^ \hat\sigma σ^越接近0,表示预测的坐标 μ ^ \hat\mu μ^周围的分布方差越小,即 μ ^ \hat\mu μ^不确定性越小。相反,关键点图片质量越低,预测出来的 σ ^ \hat\sigma σ^越不趋于0,表示预测的坐标 μ ^ \hat\mu μ^周围的分布方差越大,即 μ ^ \hat\mu μ^不确定性越大。这与真实情况是相符的。
因此,RLE通过流模型预测方差 σ \sigma σ反映模型预测坐标的不确定性,结合预测的坐标均值 μ \mu μ,RLE可以确定概率分布函数。而Regression只关心离散概率分布的均值(一个均值可以对应无数种分布),丢失了 μ \mu μ周围分布的信息,相较于heatmap显示地将GT分布(人为设置方差 σ \sigma σ)标注成高斯热图并作为学习目标,RLE隐性的极大似然损失可以帮助regression确定概率分布均值与方差,从而更好的回归坐标。
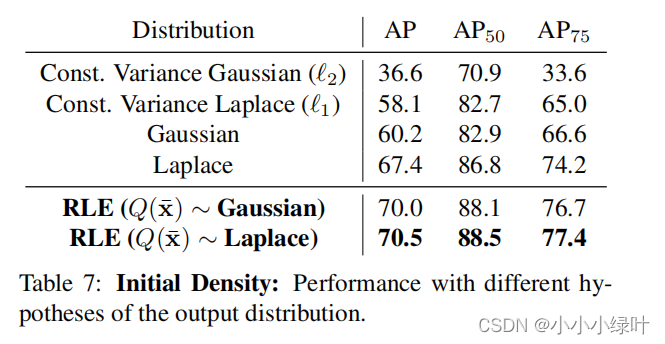
从表7中,我们可以发现,当固定高斯分布的 σ \sigma σ时,loss就退化成L2,AP降至36.6,当模型具有可学习参数 σ \sigma σ时,AP涨幅惊人。使用RLE生成概率分布可以有效提高AP。
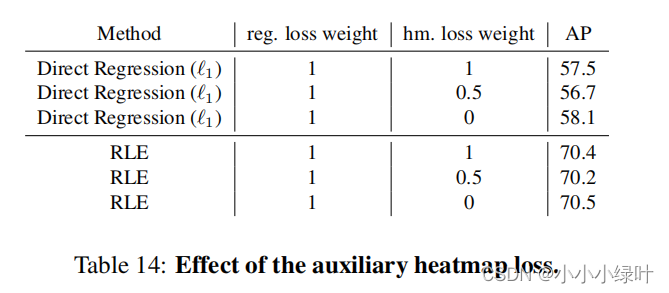
从表14中,我们可以发现,当加入heatmap loss时,Regression的性能会降低,说明heatmap 与 Regression的损失相关性不大,一定程度上可以认为时一种噪声。而在RLE中加入heatmap loss影响不大,热图显式地将这个分布标注出来,作为学习目标,而RLE则相对不那么直接地利用学习到的分布,从侧面说明,RLE极大似然损失隐性地构造概率分布可以弥补heatmap构造的显示概率分布形成的loss,提高回归性能。