目录
一,原理
回归:
假设存在一些数据点,用一条直线或者曲线或折现去拟合这些点就叫做回归。也就是找出平面点上两个轴变量之间的函数关系,或者其他坐标系下的变量间关系。一句话就是:回归就是依靠已有数据点去拟合函数关系。
常见的回归有:线性回归,非线性回归,局部加权回归……
逻辑回归:回归的目标是一个二值结果(0和1),是一种常见的二元分类模型。本质就是线性回归与激活函数sigmoid的结合,与大脑神经元工作方式类似,是入门机器学习的基础。
应用:对于一个具体的实际问题,我们可以得到他既有的一些数据,那么就可以使用逻辑回归对这些数据进行特征处理学习,让计算机去寻找处数据之间的函数关系。当我们得到新的数据,就可以应用计算机得到的函数关系去预测某些数据所产生的结果。
理论来源:
数学实现:
线性回归指的是多个y=ax+b这种的一元函数进行累加,如下面所说的数据综合体。由于需要进行分类,使用sigmoid函数将连续的线性结果人为分为0和1两种状态。
sigmoid函数:
以0.5为界限。
使用数学来实现神经元处理信息的过程:
前提:最终结果是0和1,表示两种分类结果。w(数据权重)成了模型的参数。
第一步:定义损失函数
第二步:
求解L(w)的某一个w使其函数值最小,那么与实际结果数据就越吻合。
第三步:
看这些符号已经头昏眼花。
第四步:程序实现
二,python代码
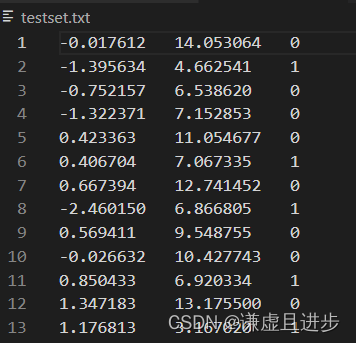
2.1 数据集的格式
命名为testset.txt,是一个N×3的形式。-0.017612与14.053064之间是一个tab的距离。
2.2 代码
import numpy as np
import matplotlib.pyplot as plt
# 定义激活函数sigmoid
def sigmoid(z):
return 1.0 / (1 + np.exp(-z))
# datas NxD
# labs Nx1
# w Dx1
# 权重更新
def weight_update(datas, labs, w, alpha=0.01):
z = np.dot(datas, w) # Nx1,神经元接受的数据综合体,有N个数据
h = sigmoid(z) # Nx1,激活函数的值,0-1之间,相对于预测值
Error = labs - h # Nx1,预测值与实际值的误差,Y-h
w = w + alpha * np.dot(datas.T, Error)
return w
#进行训练,求解参数,非随机梯度下降
def train_LR(datas, labs, n_epoch=2, alpha=0.005):
N, D = np.shape(datas)# datas NxD
w = np.ones([D, 1]) # Dx1,给权重赋初始值,都是1
# 进行n_epoch轮迭代
for i in range(n_epoch):
w = weight_update(datas, labs, w, alpha)
error_rate = test_accuracy(datas, labs, w)#计算误差率
print("epoch %d error %.3f%%" % (i, error_rate * 100))
return w
# 随机梯度下降,带batchsize的,可以使更快的找到导数为0的点,而不会在此左右徘徊,alpha也不能取太大,导致在导数为0的点处左右徘徊
def train_LR_batch(datas, labs, batchsize, n_epoch=2, alpha=0.005):
N, D = np.shape(datas)
# weight 初始化
w = np.ones([D, 1]) # Dx1
N_batch = N // batchsize
for i in range(n_epoch):
# 数据打乱
rand_index = np.random.permutation(N).tolist()
# 每个batch 更新一下weight
for j in range(N_batch):
# alpha = 4.0/(i+j+1) +0.01
index = rand_index[j * batchsize:(j + 1) * batchsize]
batch_datas = datas[index]
batch_labs = labs[index]
w = weight_update(batch_datas, batch_labs, w, alpha)
error = test_accuracy(datas, labs, w)
print("epoch %d 误差率 %.2f%%" % (i, error * 100))
return w
# 测试精确性,与模型无关,用于提醒展示效果,作用是计算误差率
def test_accuracy(datas, labs, w):
N, D = np.shape(datas)
z = np.dot(datas, w) # Nx1
h = sigmoid(z) # Nx1
lab_det = (h > 0.5).astype(np.float)
error_rate = np.sum(np.abs(labs - lab_det)) / N
return error_rate
# 画图,直观地表示出结果
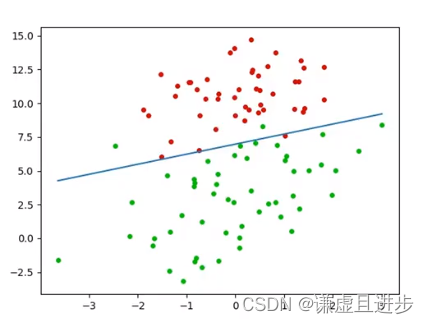
def draw_desion_line(datas, labs, w, name="0.jpg"):
dic_colors = {0: (.8, 0, 0), 1: (0, .8, 0)}
# 画数据点
for i in range(2):
index = np.where(labs == i)[0]
sub_datas = datas[index]
plt.scatter(sub_datas[:, 1], sub_datas[:, 2], s=16., color=dic_colors[i])
# 画判决线
min_x = np.min(datas[:, 1])
max_x = np.max(datas[:, 1])
w = w[:, 0]
x = np.arange(min_x, max_x, 0.01)
y = -(x * w[1] + w[0]) / w[2]
plt.plot(x, y)
plt.savefig(name)
#加载数据集进行训练或者加载测试数据对模型进行检验
def load_dataset(file):
with open(file, "r", encoding="utf-8") as f:
lines = f.read().splitlines()
# 取 lab 维度为 N x 1
labs = [line.split("\t")[-1] for line in lines]
labs = np.array(labs).astype(np.float32)
labs = np.expand_dims(labs, axis=-1) # Nx1
# 取数据 增加 一维全是1的特征
datas = [line.split("\t")[:-1] for line in lines]
datas = np.array(datas).astype(np.float32)
N, D = np.shape(datas)
# 增加一个维度
datas = np.c_[np.ones([N, 1]), datas]
return datas, labs
if __name__ == "__main__":
# 加载数据
file = "1.txt"
datas, labs = load_dataset(file)
weights = train_LR_batch(datas, labs,batchsize=2, alpha=0.001, n_epoch=800)
print('w1是{},w2是{},b是{}'.format(weights[0][0],weights[1][0],weights[2][0]))
#回归直线就是w1x+w2y+b=0
draw_desion_line(datas, labs, weights, name="test_1.jpg")#将结果保存为jpg文件
三,适用条件
多用于二维平面点集的分类,当数据集维度过大,逻辑回归的效果并不好,无法使交叉熵趋于0。