目录
1 二叉树的定义与性质
1.1 递归定义
通俗来讲,二叉树由许多个节点构成,每个节点存储一个数据,位于二叉树顶层的节点称为根节点(root)。根节点指向两个孩子节点(child),分别叫做左孩子和右孩子,两个孩子节点互为兄弟(siblings)。相应的,根节点叫做这两个孩子节点的父节点(parent)。以这两个孩子节点作为根节点,又组成了两个子树(subtree)。这两个子树也是二叉树,分别叫做左子树和右子树。
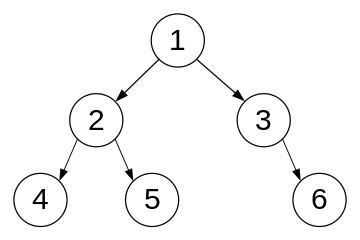
上图是一个二叉树的实例,每个圆圈代表一个节点,圆圈中的数字表示节点中存储的数据。根据上面的定义,包含数据 2 的节点是包含数据 4 节点的父节点,包含数据 3 的节点的左孩子为空节点,包含数据 4 的节点的兄弟节点为包含数据 5 的节点。
由上面的例子可以看出,二叉树的内容有且只有以下两种情况:
- 为空节点;
- 为一个根节点,根节点包含数据和另外两个二叉树。
下面的伪代码定义了二叉树的这两种情况:
BinaryTree = null //空节点
BinaryTree = {
data; // 节点存储的数据
BinaryTree left; // 左子树
BinaryTree right; // 右子树
}
通过观察可以发现,上述二叉树的定义中又包含了二叉树的定义,因此这是一个递归的定义。这种递归定义体现出了二叉树的递归结构。
根据上面的伪代码,我们可以用下面的 Python 代码定义二叉树:
class BinaryTree: def __init__(self, data): # 左子树 self.left = None # 右子树 self.right = None # 该树的根节点存储的数据 self.data = data class Node: def __init__(self, data): # 左孩子 self.left = None # 右孩子 self.right = None # 该节点存储的数据 self.data = data
值得注意的是,上面的代码给出了二叉树的两种定义方式。从代码中可以看出,这两种定义命名不同,但代码结构是完全等价的(都只包含三个成员:left, right 和 data),因此这两种定义是等价的。
之所以说这两种定义是等价的,原理在于我们只需要根节点的信息来表示一棵二叉树,因此 Node 类和 BinaryTree 类都可以表示出二叉树所有的信息。许多其他教程采用的是 Node 类的定义方式。下文中我们统一使用 Node 类来表示二叉树。
上图的二叉树可以通过下列 Python 代码进行构造:
node1 = Node(1) node2 = Node(2) node3 = Node(3) node2.left = Node(4) node2.right = Node(5) node3.right = Node(6) node1.left = node2 node1.right = node3 tree = node1
1.2 二叉树的高度、层数
在二叉树中,两个孩子节点都为空的节点称为叶子节点(leaf)。二叉树中,节点的高度(height)定义为从叶子节点到该节点的最大距离。因此,上图中包含数据 4 的节点的高度为 0,包含数据 2 的节点的高度为 1,根节点的高度为 2。此外,二叉树的高度定义为根节点的高度,所以上图二叉树的高度为 2。
节点的层数(level)定义为该节点到根节点的距离+1。因此在上图中,根节点的层数为 1,包含数据 4 的节点的层数为 3。
不难发现,二叉树具有以下性质:
- 二叉树的第 i 层至多有 2i-1个节点;
- 高度为 h 的二叉树至多有 2h 个叶子节点,至多有 2h+1-1 个节点;
- 具有 n 个节点的二叉树至少具有高度⌈log2n+1-1⌉。
2 二叉树的遍历
为了取得二叉树上存储的数据,我们通常从二叉树的根节点开始,按照一定的顺序,对树上的每个节点进行一次访问。访问的过程称为二叉树的遍历(traversal)。根据访问节点的顺序不同,通常使用的二叉树遍历可以分为前序遍历(preorder traversal)、中序遍历(inorder traversal)和后序遍历(postorder traversal)。
对上图的二叉树进行这三种遍历,节点的遍历顺序为:
- 先序遍历(根、左、右):1,2,4,5,3,6;
- 中序遍历(左、根、右):4,2,5,1,3,6;
- 后序遍历(左、右、根):4,5,2,6,3,1。
2.1 递归遍历算法
根据二叉树的递归定义,我们很容易得到这三种遍历的递归算法。因为二叉树的内容或为空,或为根节点,因此递归算法只需针对这两种情况进行相应处理就能保证算法的正确性。下面是使用这三种遍历打印二叉树的 Python 代码:
def preorder_print(root): if root == None: return else: # 根节点 -> 左子树 -> 右子树 print(root.data) preorder_print(root.left) preorder_print(root.right) def inorder_print(root): if root == None: return else: # 左子树 -> 根节点 -> 右子树 inorder_print(root.left) print(root.data) inorder_print(root.right) def postorder_print(root): if root == None: return else: # 左子树 -> 右子树 -> 根节点 postorder_print(root.left) postorder_print(root.right) print(root.data)
若二叉树的总节点数为 n,高度为 h,则上述递归算法的时间复杂度均为 O(n)。若考虑递归函数调用消耗的栈空间,则空间复杂度为 O(h)。
2.2 迭代遍历算法
由于递归算法的函数调用对算法运行的时间和空间开销都有较大影响,因此我们可以将递归算法转化为迭代算法(iteration),使用循环代替递归调用。转化后的迭代算法需要一个额外的栈(stack)作为辅助。
下面分别是前序、中序和后序遍历迭代算法的 Python 代码:
def preorder_print_with_stack(root): stack = [] stack.append(root) while stack: current = stack.pop() print(current.data) if current.right: stack.append(current.right) if current.left: stack.append(current.left) def inorder_print_with_stack(root): stack = [] current = root while True: if current: stack.append(current) current = current.left elif stack: current = stack.pop() print(current.data) current = current.right else: break def postorder_print_with_stack(root): stack = [] current = root while True: if current: stack.append(current) current = current.left elif stack: peek = stack[-1] if peek.right: current = peek.right else: previous = stack.pop() print(previous.data) while stack and previous == stack[-1].right: previous = stack.pop() print(previous.data) else: break
若二叉树的总节点数为 n,高度为 h,则上述迭代算法的时间复杂度为 O(n),额外栈需要的空间复杂度为 O(h)。尽管迭代算法和递归算法的时间复杂度都为 O(n),空间复杂度也同为 O(h),但是递归算法复杂度的常数系数通常会更大,所以迭代算法的实际运行效率会更高。
2.3 Morris 迭代遍历
此外,上述的迭代算法还可以进一步优化,使其不需要额外的栈空间,优化了算法的空间复杂度。这种迭代算法称为 Morris 遍历算法。Morris 算法在遍历时会修改二叉树的结构以保存路径信息,遍历之后再恢复成原来的二叉树。因此 Morris 算法的空间复杂度为 O(1),时间复杂度依然为 O(n)。
def preorder_print_morris(root): current = root while current: if not current.left: print(current.data) current = current.right else: # 找到 current 的左子树最右端,即前驱节点 predecessor = current.left while predecessor.right != current and predecessor.right: predecessor = predecessor.right if predecessor.right == None: # 此时左子树还没遍历,令前驱节点的右孩子指向 current 节点 predecessor.right = current print(current.data) current = current.left else: # 此时左子树遍历完成,恢复前驱节点的右孩子 predecessor.right = None current = current.right # 与上面算法打印 current 的时机不同,其余完全一致 def inorder_print_morris(root): current = root while current: if not current.left: print(current.data) current = current.right else: predecessor = current.left while predecessor.right != current and predecessor.right: predecessor = predecessor.right if predecessor.right == None: predecessor.right = current current = current.left else: predecessor.right = None print(current.data) current = current.right
Morris 后序遍历算法与上面算法类似,只有两点不同:
- 需要一个额外的辅助函数用来反向打印;
- 算法的开头增加了一个辅助节点 dummy,把原来的二叉树作为辅助节点的左子树,用来使算法可以正确遍历原二叉树的右子树。
下面是前序和中序遍历的 Morris 算法的 Python 代码:
def reverse_print(begin, end): # 反转链表 current = begin.right pre = begin end = end.right while current != end: tmp = current.right current.right = pre pre, current = current, tmp # 反向打印并恢复链表 pre, current = current, pre while current != begin: print(current.data) tmp = current.right current.right = pre pre, current = current, tmp print(begin.data) def postorder_print_morris(root): dummy = Node(None) dummy.left = root current = dummy while current: if not current.left: current = current.right else: predecessor = current.left while predecessor.right != current and predecessor.right: predecessor = predecessor.right if predecessor.right == None: predecessor.right = current current = current.left else: predecessor.right = None reverse_print(current.left, predecessor) current = current.right
3 相关问题
3.1 判断两个二叉树是否相同
类比先序遍历。先判断根节点是否相同,再递归判断左子树和右子树。算法对每个节点都进行了一次比较,因此时间复杂度为 O(n)。
def is_equal(r1, r2): if not r1 and not r2: return True elif not r1 or not r2: return False else: return (r1.data == r2.data and is_equal(r1.left, r1.left) and is_equal(r1.right, r2.right))
3.2 计算二叉树的大小(高度、最大值、最小值)
类比后序遍历。先递归计算左子树和右子树的值,再计算出根节点的值。计算高度、最大值、最小值等性质的算法与计算大小的算法类似。算法对每个节点都进行了一次计算,因此时间复杂度是 O(n)。下面是计算大小的 Python 代码:
def get_size(root): if not root: return 0 else: return get_size(root.left) + get_size(root.right) + 1
3.3 求两个节点的最近公共祖先
如果树中不包含这两个节点,则公共祖先为空;如果根节点等于这两个节点中的任意一个,则最近公共祖先为根节点;如果两个子树的最近公共祖先都不为空,则最近公共祖先为根节点。算法的时间复杂度为 O(n)。Python 代码如下:
def lowest_common_ancestor(root, a, b): if not root: return None if root == a or root == b: return root left = lowest_common_ancestor(root.left, a, b) right = lowest_common_ancestor(root.right, a, b) if left and right: return root elif left: return left else: return right
3.4 逐层遍历(从上到下、从下到上、蛇形)
利用一个额外的队列。初始化时将根节点加入队列,然后从队列头循环取出节点,把节点的左孩子和右孩子依次加入队列末尾,直到队列为空。下面是从上到下逐层遍历的 Python 代码:
def levelbylevel_topdown(root): if not root: return from collections import deque queue = deque() queue.append(root) while queue: current = queue.popleft() print(current.data) if current.left: queue.append(current.left) if current.right: queue.append(current.right)
如果要从下到上逐层遍历,那么还需要一个额外的栈。修改上面的算法,令右孩子先入队,同时把打印结果替换成结果压入栈,遍历完之后把结果依次弹出栈。出栈的顺序即为从下到上逐层遍历的顺序。
蛇形逐层遍历具有先进先出的特点,可以使用两个栈来实现。队列的两头都可以进出,所以可以使用队列来模拟两个栈。此外队列的实现需要标记二叉树每层的末尾,以便在遍历到每层末尾时,交换取节点和加节点的位置。标记的方法有许多种,可以使用计数器记录每层节点的个数,也可以在末尾添加分隔符。下面的代码采用分隔符法。
def spiral_print(root): if not root: return from collections import deque queue = deque() queue.append(root) queue.append(None) while len(queue) > 1: # 头部取节点,尾部加节点 current = queue[0] while current: queue.popleft() print(current.data) if current.left: queue.append(current.left) if current.right: queue.append(current.right) current = queue[0] # 遇到分隔符,变成尾部取节点,头部加节点 current = queue[-1] while current: queue.pop() print(current.data) if current.right: queue.appendleft(current.right) if current.left: queue.appendleft(current.left) current = queue[-1]
以上算法对于每个节点都只遍历一次,因此时间复杂度为 O(n)。
3.5 根据遍历结果还原二叉树
根据二叉树前序和中序遍历的结果,我们可以还原出二叉树的结构。算法假设二叉树中没有重复的节点。首先我们知道前序遍历的第一个节点为根节点,在中序遍历里查找根节点出现的索引。那么以根节点为界,在中序遍历中根节点之前的节点都属于左子树,之后的节点属于右子树。相似的,我们把前序遍历也分成左右两部分。最后,递归构造左右子树,得到最终结果。
根据后序和中序遍历的结果同样也能还原二叉树,原理和上述算法类似。然而前序和后序遍历的结果无法还原二叉树,原因在于左右子树节点的分界点只能通过中序遍历的结果得出。
下面是这两种算法的 Python 代码。值得注意的是,如果使用一维搜索查找根节点的索引,那么算法的总体复杂度为 O(n2)。因此下面的算法使用字典来优化查找根节点索引,优化后的算法时间复杂度为 O(n):
def build_from_inorder_preorder(inorder, preorder): index = {x:i for i, x in enumerate(inorder)} def build_from_range(in_begin, in_end, pre_begin, pre_end): if in_begin > in_end or pre_begin > pre_end: return None data = preorder[pre_begin] root_index = index[data] root = Node(data) root.left = build_from_range(in_begin, root_index - 1, pre_begin + 1, pre_begin + (root_index - in_begin)) root.right = build_from_range(root_index + 1, in_end, pre_begin + (root_index - in_begin) + 1, pre_end) return root return build_from_range(0, len(inorder)-1, 0, len(preorder)-1) def build_from_inorder_postorder(inorder, postorder): index = {x:i for i, x in enumerate(inorder)} def build_from_range(in_begin, in_end, post_begin, post_end): if in_begin > in_end or post_begin > post_end: return None data = postorder[post_end] root_index = index[data] root = Node(data) root.left = build_from_range(in_begin, root_index - 1, post_begin, post_begin + (root_index - in_begin) - 1) root.right = build_from_range(root_index + 1, in_end, post_begin + (root_index - in_begin), post_end - 1) return root return build_from_range(0, len(inorder)-1, 0, len(postorder)-1)