文章和代码已经归档至【Github仓库:algorithms-notes】或者公众号【AIShareLab】回复 算法笔记 也可获取。
贪心的核心思想:最优解,短视。
按照数据规模猜测贪心,一般在 1 0 5 10 ^ 5 105是排序, 1 0 6 10 ^ 6 106或 1 0 7 10 ^ 7 107是O(n)的做法,扫描一边,1000左右是两重循环,100左右是三重循环。
股票买卖 II
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
输入格式
第一行包含整数 N,表示数组长度。
第二行包含 N 个不大于 10000 的正整数,表示完整的数组。

输出格式
输出一个整数,表示最大利润。
数据范围
1 ≤ N ≤ 1 0 5 1≤N≤10^5 1≤N≤105
输入样例1:
6
7 1 5 3 6 4
输出样例1:
7
输入样例2:
5
1 2 3 4 5
输出样例2:
4
输入样例3:
5
7 6 4 3 1
输出样例3:
0
样例解释
样例1:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。共得利润 4+3 = 7。
样例2:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
样例3:在这种情况下, 不进行任何交易, 所以最大利润为 0。
贪心思路:
任何跨度大于一天的交易都可以拆分成跨度等于一天的交易(中间部分的买和卖相互抵消了)。所以最优解只需要聚焦在这跨度为1的交易上即可,那么基本思路就是如果后一天价格大于前一天,则交易一次。
code
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int price[N];
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i ++ )scanf("%d", &price[i]);
int res = 0;
for(int i = 0; i + 1 < n; i ++ )
{
int dt = price[i + 1] - price[i];
if(dt > 0) res += dt;
}
printf("%d", res);
}
货仓选址
在一条数轴上有 N 家商店,它们的坐标分别为 A 1 A_1 A1∼ A N A_N AN。
现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。
为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
输入格式
第一行输入整数 N。
第二行 N 个整数 A 1 A_1 A1∼ A N A_N AN。
输出格式
输出一个整数,表示距离之和的最小值。
数据范围
1 ≤ N ≤ 100000 1≤N≤100000 1≤N≤100000,
0 ≤ A i ≤ 40000 0≤A_i≤40000 0≤Ai≤40000
输入样例:
4
6 2 9 1
输出样例:
12
思路:
中位数有非常优秀的性质,比如说在这道题目中,每一个点到中位数的距离,都是满足全局的最有性,而不是局部最优性。
具体的来说,我们设在仓库左边的所有点,到仓库的距离之和为p,右边的距离之和则为q,那么我们就必须让p+q的值尽量小。
当仓库向左移动的话,p会减少x,但是q会增加n−x,所以说当为仓库中位数的时候,p+q最小。

每次只关注局部最优解,即可推出全局最优解。
code
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100010;
int x[N];
int n;
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i ++ ) scanf("%d", &x[i]);
// 首先需要进行排序
sort(x, x + n);
// 这里求中点采用下取整的方式,
// 可以举例eg:n = 3,则0 1 2 3,中点为[3/2]=1即可(在两者之间即为最短)。
int c = x[n / 2];
LL res = 0;
for (int i = 0; i < n; i ++ ) res += abs(x[i] - c);
printf("%lld", res);
return 0;
}
糖果传递
有 n 个小朋友坐成一圈,每人有 a[i] 个糖果。
每人只能给左右两人传递糖果。
每人每次传递一个糖果代价为 1。
求使所有人获得均等糖果的最小代价。
输入格式
第一行输入一个正整数 n,表示小朋友的个数。
接下来 n 行,每行一个整数 a[i],表示第 i 个小朋友初始得到的糖果的颗数。
输出格式
输出一个整数,表示最小代价。
数据范围
1 ≤ n ≤ 1000000 1≤n≤1000000 1≤n≤1000000,
0 ≤ a [ i ] ≤ 2 × 1 0 9 0≤a[i]≤2×10^9 0≤a[i]≤2×109,
数据保证一定有解。
输入样例:
4
1
2
5
4
输出样例:
4
思路:
题目可以绘图如下:

其中:
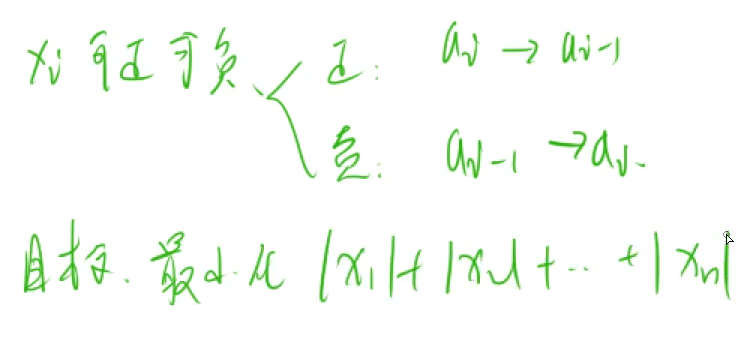
那么可以看到:


由上式,可以归纳出:
c i = c i + 1 + a ˉ − a i c_{i}=c_{i+1}+\bar{a}-a_{i} ci=ci+1+aˉ−ai
那么原目标函数可以化简为:

这样就转换成与上一题一样的思想了。
code
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1000010;
int n;
int a[N];
LL c[N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
LL sum = 0;
for (int i = 1; i <= n; i ++ ) sum += a[i];
LL avg = sum / n;
for (int i = n; i > 1; i -- )
{
c[i] = c[i + 1] + avg - a[i];
}
c[1] = 0;
sort(c + 1, c + n + 1);
LL res = 0;
// 由于i从1开始,因此取中点时,c[(n + 1) / 2],相当于上取整
for (int i = 1; i <= n; i ++ ) res += abs(c[i] - c[(n + 1) / 2]);
printf("%lld\n", res);
return 0;
}
雷达设备
假设海岸是一条无限长的直线,陆地位于海岸的一侧,海洋位于另外一侧。
每个小岛都位于海洋一侧的某个点上。
雷达装置均位于海岸线上,且雷达的监测范围为 d,当小岛与某雷达的距离不超过 d 时,该小岛可以被雷达覆盖。
我们使用笛卡尔坐标系,定义海岸线为 x 轴,海的一侧在 x 轴上方,陆地一侧在 x 轴下方。
现在给出每个小岛的具体坐标以及雷达的检测范围,请你求出能够使所有小岛都被雷达覆盖所需的最小雷达数目。
输入格式
第一行输入两个整数 n 和 d,分别代表小岛数目和雷达检测范围。
接下来 n 行,每行输入两个整数,分别代表小岛的 x,y 轴坐标。
同一行数据之间用空格隔开。
输出格式
输出一个整数,代表所需的最小雷达数目,若没有解决方案则所需数目输出 −1。
数据范围
1 ≤ n ≤ 1000 1≤n≤1000 1≤n≤1000,
− 1000 ≤ x , y ≤ 1000 −1000≤x,y≤1000 −1000≤x,y≤1000
输入样例:
3 2
1 2
-3 1
2 1
输出样例:
2
思路:

给定若干区间,最少选择多少个点,可以使每个区间上最少选一个点?
贪心策略:
-
将所有区间按右端点从小到大排序;
-
依次考虑每个区间:
-
如果当前区间包含最后一个选择的点,则直接跳过;
-
如果当前区间不包含最后一个选择的点,则在当前区间的右端点的位置选一个新的点;
-
证明:
cnt:算法得到的结果
opt:最优解
最优解表示所有方法的最小值,因此 o p t ≤ c n t opt \le cnt opt≤cnt 。
再证明 o p t ≥ c n t opt \ge cnt opt≥cnt :
- 所有可行解必然都大于等于cnt:选了cnt个点,则意味着必然存在cnt个互不相交的区间。
首先上述做法一定可以保证所有区间都至少包含一个点。
然后我们再证明这样选出的点的数量是最少的,不妨设选出的点数是 m:
按照上述做法,我们选择的点都是某个区间的右端点,而且由于区间按右端点排好序了,所以我们选择的点也是排好序的;
只有在当前区间和上一个点所对应的区间是没有交集时,我们才会选择一个新点,所以所有选出的点所对应的区间是如下图所示的情况,两两之间没有交集。
所以我们找到了 m 个两两之间没有交集的区间,因此我们至少需要选 m 个点。而且通过上述做法,我们可以只选 m 个点。因此最优解就是 m。
时间复杂度
-
计算每个坐标所对应的区间,需要 O(n)的计算量;
-
将所有区间排序需要 O(nlogn) 的计算量;
-
扫描所有区间需要 O(n)的计算量;
所以总共的时间复杂度是 O(nlogn)。
code:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 1010;
int n, d;
// 用stl的pair也可以,这里自己定义结构 segment 了
struct Segment
{
double l, r;
// 重载比较符
bool operator< (const Segment& t) const
{
return r < t.r;
}
}seg[N];
int main()
{
scanf("%d%d", &n, &d);
bool failed = false;
for (int i = 0; i < n; i ++ )
{
int x, y;
scanf("%d%d", &x, &y);
// 离海岸线大于d,则不可能存在,因此失败
if (y > d) failed = true;
else
{
// 计算线段长度
double len = sqrt(d * d - y * y);
// 左右端点
seg[i].l = x - len, seg[i].r = x + len;
}
}
if (failed)
{
puts("-1");
}
else
{
sort(seg, seg + n);
int cnt = 0;
double last = -1e20;
for (int i = 0; i < n; i ++ )
// last 小于左边界,则增加右边界的点
if (last < seg[i].l)
{
cnt ++ ;
last = seg[i].r;
}
printf("%d\n", cnt);
}
return 0;
}