变换
线性变换
线性变换的定义
先来研究一下数学函数 τ ( v ) = τ ( x , y , z ) = ( x ′ , y ′ , z ′ ) τ(v) = τ(x, y, z) = (x^′, y^′, z^′) τ(v)=τ(x,y,z)=(x′,y′,z′)。此函数输入输出都是向量。我们称 τ τ τ为线性变换,当且仅当函数具有下列性质时候:
τ ( u + v ) = τ ( u ) + τ ( v ) τ(u+v) = τ(u)+τ(v) τ(u+v)=τ(u)+τ(v)
τ ( k v ) = τ ( u ) + k τ ( v ) τ(kv) = τ(u)+kτ(v) τ(kv)=τ(u)+kτ(v)
( u 、 v u、v u、v为向量, k k k为标量)
易得:
如果 τ τ τ是线性函数,那么有:

矩阵表示法
设 u = ( x , y , z ) , i = ( 1 , 0 , 0 ) , j = ( 0 , 1 , 0 ) , k = ( 0 , 0 , 1 ) ( i , j , k , 表示坐标轴上三个方向的单位向量,叫做标准基向量) u=(x,y,z),i=(1,0,0),j=(0,1,0),k=(0,0,1)(i,j,k,表示坐标轴上三个方向的单位向量,叫做标准基向量) u=(x,y,z),i=(1,0,0),j=(0,1,0),k=(0,0,1)(i,j,k,表示坐标轴上三个方向的单位向量,叫做标准基向量):
u = ( x , y , z ) = x i + y j + z k x = x ( 1 , 0 , 0 ) + y ( 0 , 1 , 0 ) + z ( 0 , 0 , i ) u=(x,y,z)=xi+yj+zkx=x(1,0,0)+y(0,1,0)+z(0,0,i) u=(x,y,z)=xi+yj+zkx=x(1,0,0)+y(0,1,0)+z(0,0,i)
假设 τ τ τ是一条线性曲线,由上面公式可得:
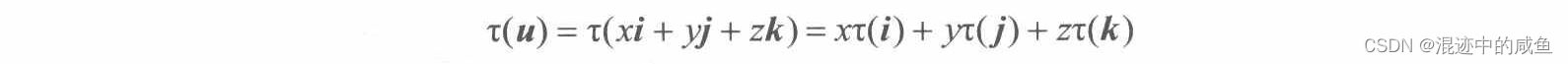
结合矩阵的公式:
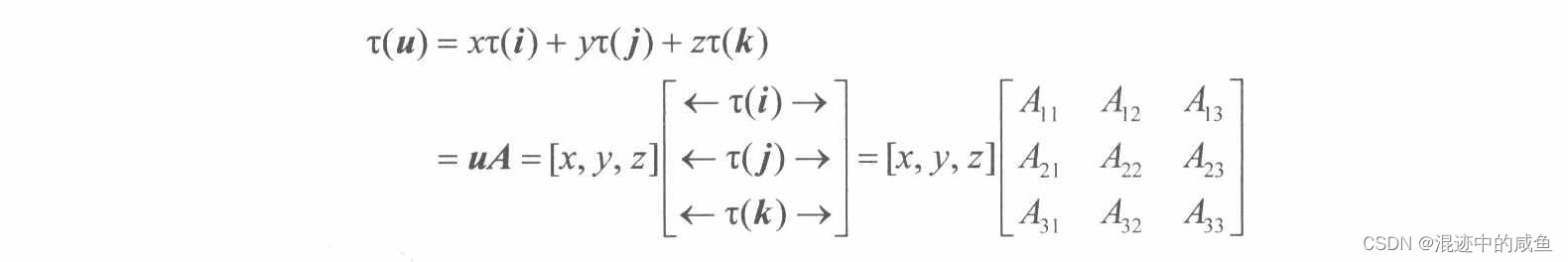
τ ( i ) = τ ( A 11 , A 12 , A 13 ) τ(i) = τ(A_{11}, A_{12}, A_{13}) τ(i)=τ(A11,A12,A13), τ ( j ) = τ ( A 21 , A 22 , A 23 ) τ(j) = τ(A_{21}, A_{22}, A_{23}) τ(j)=τ(A21,A22,A23), τ ( k ) = τ ( A 31 , A 32 , A 33 ) τ(k) = τ(A_{31}, A_{32}, A_{33}) τ(k)=τ(A31,A32,A33),这时候的 A A A我们可以称之为矩阵 τ τ τ的线性变换的矩阵表示法。
缩放矩阵
缩放的计算常见于游戏中,比如获得增益体型增大等等。
在这我们先放置缩放矩阵,再进行逆推:
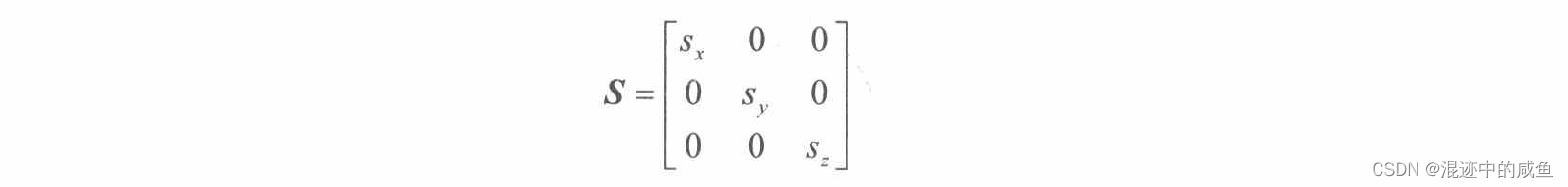
假设我们有一个立方体边长为4,那么我们得到了一个向量 [ 4 , 4 , 4 ] \;[4,4,4]\; [4,4,4],这时候我们想在 x x x轴放大2倍, y y y轴缩小俩倍,z轴放大5倍,那么这时候我们有个缩放矩阵: [ 2 0 0 0 0.5 0 0 0 5 ] \left[\begin{array}{ccc}2 & 0 & 0 \\0 & 0.5 & 0 \\0 & 0 & 5\end{array}\right] ⎣
⎡20000.50005⎦
⎤这时候,我们用向量乘矩阵的计算则有:
[ 4 , 4 , 4 ] [ 2 0 0 0 0.5 0 0 0 5 ] = [ 8 , 2 , 20 ] [4,4,4]\left[\begin{array}{ccc}2 & 0 & 0 \\0 & 0.5 & 0 \\0 & 0 & 5\end{array}\right]=[8,2,20] [4,4,4]⎣
⎡20000.50005⎦
⎤=[8,2,20]
这时候通过计算验证,也成功得到了我们想要缩放之后的结果。
再假设一个坐标[-4,-4,0],我们要让他在 x x x轴缩小俩倍, y y y轴放大俩倍, z z z轴不变,同样的计算:
[ − 4 , − 4 , 0 ] [ 0.5 0 0 0 2 0 0 0 1 ] = [ 2 , 8 , 0 ] [-4,-4,0]\left[\begin{array}{ccc}0.5 & 0 & 0 \\0 & 2 & 0 \\0 & 0 & 1\end{array}\right]=[2,8,0] [−4,−4,0]⎣
⎡0.500020001⎦
⎤=[2,8,0]
最终也一致的得到我们想要的结果。
变换过程如下图所示:
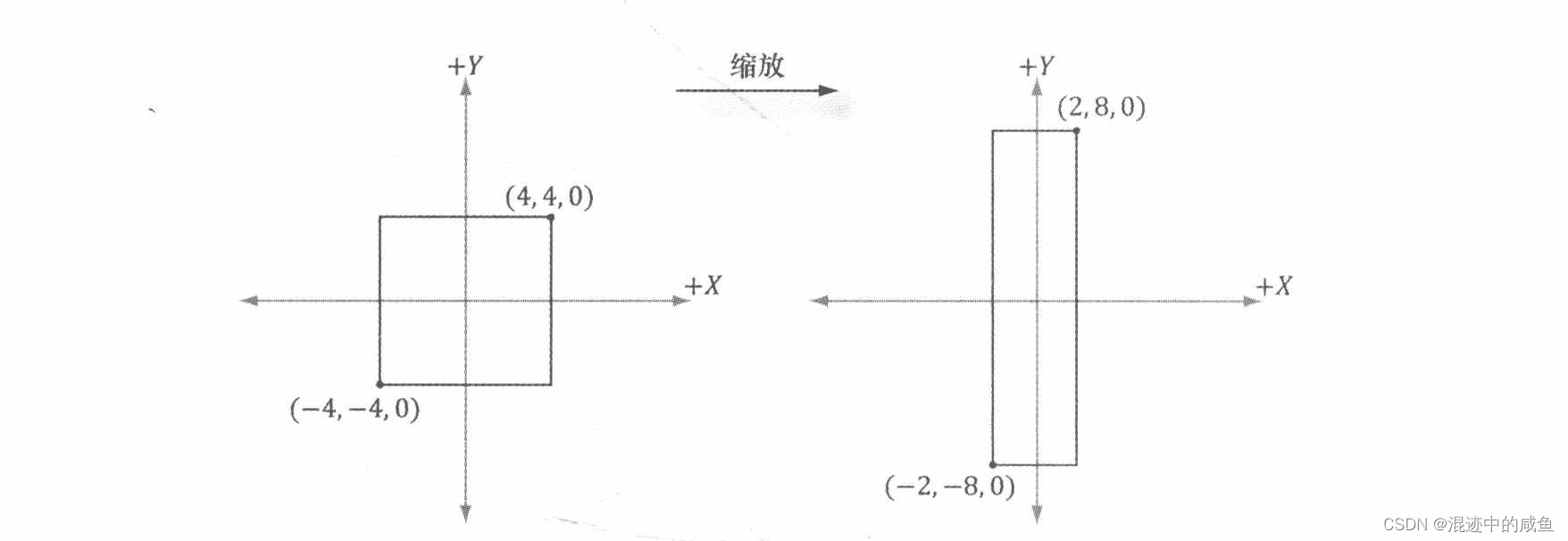
旋转矩阵
旋转矩阵公式
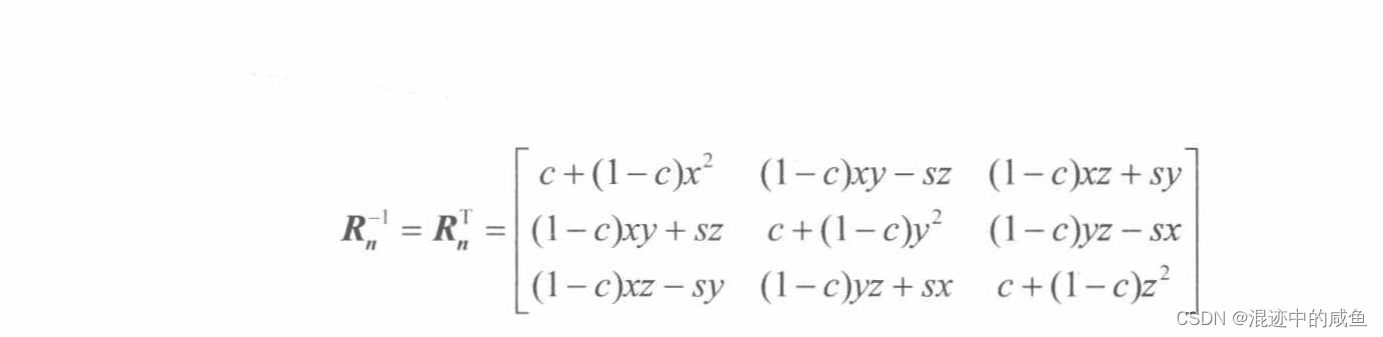
对于矩阵公式的推导(整个推导过程较为复杂,关心的朋友可以自己去看看原版的推导过程),我们其实不怎么关注,下面就直接放公式,分别是对于 x , y , z x,y,z x,y,z轴的旋转
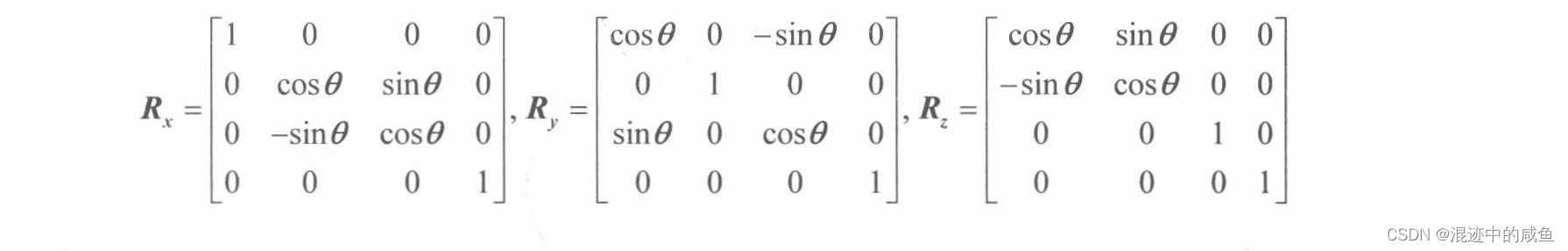
仿射变换
齐次坐标
向量的平移是没意义的,因为,它只有大小和方向,与位置无关,而齐次坐标这个概念就能帮我处理向量的问,我们采用其次方式,将坐标扩充为四元组,第四个坐标 w w w的取值根据被描述对象是点还是向量而定。
1. ( x , y , z , 0 ) (x,y,z,0) (x,y,z,0)表示向量
2. ( x , y , z , 1 ) (x,y,z,1) (x,y,z,1)表示点
仿射变换的定义以及其矩阵表示
一个线性变换与平移变换的组合,放射变换不能表示出我们需要的所有变换,因此在其中添加一个平移向量 b b b
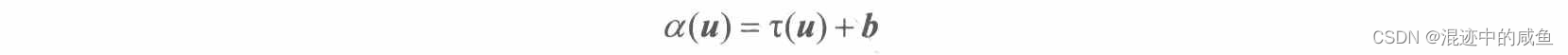

平移变换
蚂蚁借助位移向量 b b b进行位移,现将平移变换定义为仿射变换:

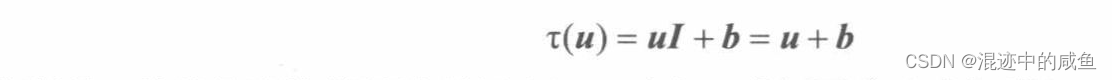
最终有:
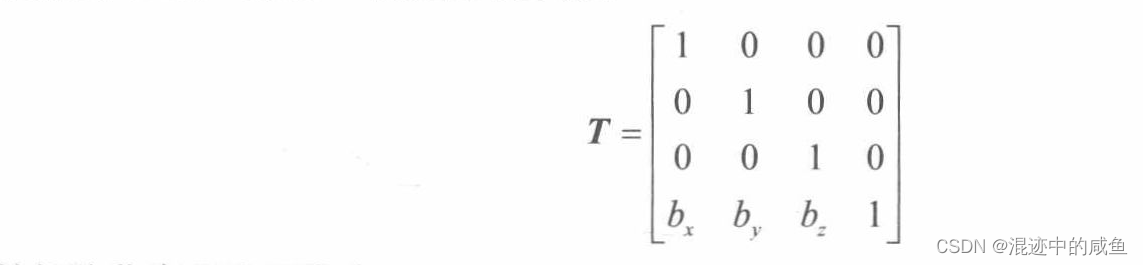
该矩阵就是平移矩阵(数据计算的验证过程,大家就可以自己去试试了)。
缩放和旋转的放射矩阵
我们将平移选择结合到一起则有:
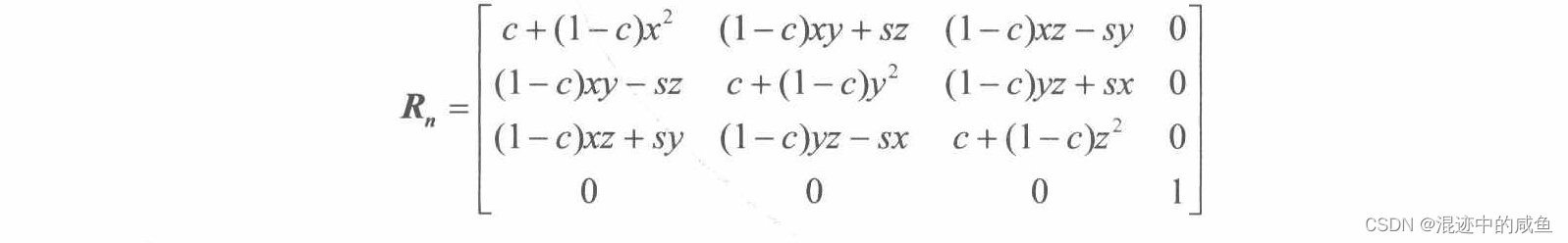
变换的复合
下面试俩种变换方式
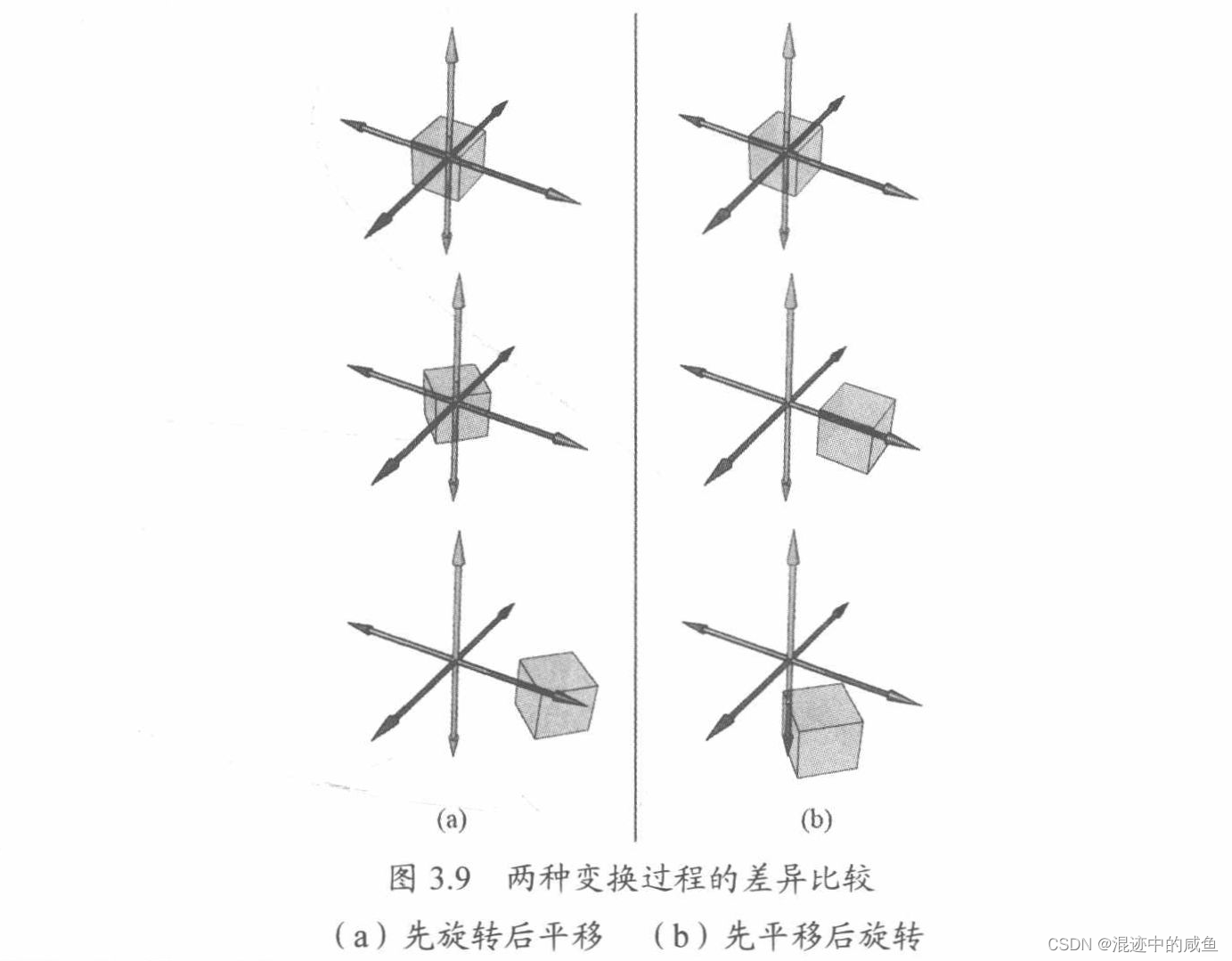
在大多计算中,都是先把物体移动到原点,然后做自身的旋转,最后再平移,这才是我们想要的结果,当然,如果要围绕着某个轴旋转那例外。
标架的矩阵

DriectXMath库提供的变换函数
//构建缩放矩阵
XMMATRIX XM_CALLCONV XMMatrixScaling(
float ScaleX,
float ScaleY,
float ScaleZ);
//用缩放系数构建缩放矩阵
XMMATRIX XM_CALLCONV XMMatrixScalingFromVector(FXMVECTOR Scale);
XMMATRIX XM_CALLCONV XMMatrixRotationX(float Angle);
XMMATRIX XM_CALLCONV XMMatrixRotationY(float Angle);
XMMATRIX XM_CALLCONV XMMatrixRotationZ(float Angle);
XMMATRIX XM_CALLCONV XMMatrixRotationAxis(FXMVECTOR Axis, float Angle);
XMMATRIX XM_CALLCONV XMMatrixTranslation(float OffsetX,float OffsetY,float OffsetZ);
XMMATRIX XM_CALLCONV XMMatrixTranslationFromVector(FXMVECTOR Offset);//用3D向量中的一个分类来构建平移矩阵
XMVECTOR XM_CALLCONV XMVector3TransformCoord(FXMVECTOR V, CXMMATRIX M); //计算点与矩阵乘积
XMVECTOR XM_CALLCONV XMVector3TransformNormal(FXMVECTOR V, CXMMATRIX M); //计算向量矩阵乘积