CS224W课程学习笔记（一）：课程介绍与图深度学习概念

引言

我们从怎么利用图形或网络表示数据这一动机开始。网络成为了用于描述复杂系统中交互实体的通用语言。从图片上讲，与其认为我们的数据集由一组孤立的数据点组成，不如考虑这些点之间的相互作用和关系。

在不同种类的网络之间进行哲学上的区分是有启发性的。对网络的一种解释是作为现实生活中出现的现象的例子。我们称这些网络为 natural graphs 。比如：

• 人类社交网络(70多亿个体的集合)
• 互联网通信系统(电子设备的集合)

网络的另一种解释是作为一种可用于解决特定预测问题的数据结构。在这种情况下，我们对实体之间的关系更为感兴趣，因此我们可以有效地执行学习任务。我们称这些网络为 information graphs ，比如：

• 场景图（场景中的对象如何相互关联）
• 相似性网络（连接数据集中的相似点）。

在本课程中，我们主要考虑和学习的问题涉及到此类系统的组织方式与模式属性的问题，也可以将具有丰富关系结构的数据集表示为用于许多预测任务的图形，建立在这种基础之上，我们希望明确对关系的建模以获得更好的预测性能，比如：

• 节点分类： 我们预测给定节点的类型/颜色
• 链接预测： 我们预测两个节点是否链接
• 社区检测（Community detection） ： 我们在其中识别密集链接的节点簇
• 相似度计算： 我们测量两个节点或网络的相似度

总而言之，网络是一种描述复杂数据的通用语言，并且可以推广到各种不同的领域。随着数据可用性的增加和各种计算挑战的出现，学习网络知识可以做出各种各样的贡献。

（PS：翻译自Stanford的助教笔记，后文不再标出，原文地址：https://snap-stanford.github.io/cs224w-notes/preliminaries/introduction-graph-structure）

课程链接与相关工具介绍

官方原版视频

https://www.youtube.com/watch?v=JAB_plj2rbA&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=1

https://www.youtube.com/watch?v=JAB_plj2rbA&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=2

课程主页

Stanford官网：https://web.stanford.edu/class/cs224w

Graph Representation Learning Book：https://www.cs.mcgill.ca/~wlh/grl_book/

Lecture 1.1 - Why Graphs：https://www.youtube.com/watch?v=JAB_plj2rbA&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=1

扫描二维码关注公众号，回复： 14653215 查看本文章

图机器学习编程工具

PyG（PyTorch Geometric）：www.pyg.org

NetworkX：networkx.org

DGL (DEEP GRAPH LIBRARY)：https://www.dgl.ai/

AntV图可视化工具Graphin： graphin.antv.vision

AntV图可视化工具G6：g6.antv.antgroup.com

Echarts可视化：echarts.apache.org/examples/zh/index.html#chart-type-graphGL

医学知识图谱数据集收录站：https://bios.idea.edu.cn/

Hypercrx（Tracking, mining and insight into open source projects and developer relationships.）：https://crx.hypertrons.io/

Code Galaxies Visualization（github项目可视化开源图）：http://open-galaxy.x-lab.info/

课程大纲

cs224w本课程将聚焦图的机器学习和表示学习多个领域，课程大纲如下：

1. Traditional methods: Graphlets, Graph Kernels
2. Methods for node embeddings: DeepWalk, Node2Vec
3. Graph Neural Networks: GCN, GraphSAGE, GAT, Theory of GNNs
4. Knowledge graphs and reasoning: TransE, BetaE
5. Deep generative models for graphs
6. Applications to Biomedicine, Science, Industry
   
   

图

图的概念（非224w，实为记录DS相关）

什么是图？图是由顶点集合和顶点之间边的集合组成，通常记为$G=(V,E)$ ，其中，G表示一个图，V表示图G中顶点的有限非空集合，E表示图G中边的关系集合。若 V = { v 1 , v 2 , ⋯   , v n } V=\left\{v_1, v_2, \cdots, v_n\right\} V={ v1​,v2​,⋯,vn​}，则用$|V|$表示图G中顶点的个数，$E=\{(u,v)\mid u\in V,v\in V\}$，用$|E|$表示图G中边的条数。

注意： 线性表可以是空表，树可以是空树，但图不可以是空图。就是说，图中不能一个顶点也没有，图的顶点集V一定非空，但边集E可以为空，此时图中只有顶点而没有边。

图的类别（非224w）

图的类别有非常多种，但考虑篇幅问题，就不再这里过多介绍，等之后另开一帖，还需要把之前的一些想法记录融会贯通，再来重新总结图的各种类别应用，以及代码，这里简单整理修改了之前收集的思维导图，那么图的大致种类可分为：

其中里面的一些详细概念介绍为：

DS习题记录

顶点数：

1.例题 无向图$G$有$23$条边，度为$4$的顶点有$5$个，度为$3$的顶点有$4$个，其余都是度为$2$的顶点，则图$G$最多有()个顶点。

$A.6$

$B.15$

$C.16$

$D.21$

解：由于$\sum _{i=1}^{n}TD(v_i)=2e$，则$2\times 23=4\times 5+3\times 4+2\times v_2$，则$v_2=7$，所以最多有$5+4+7=16$个顶点。
（PS：对于具有$n$个顶点，$e$条边的无向图，$\sum _{i=1}^{n}TD(v_i)=2e$。无向图的边数两倍等于图各顶点度数的总和。）

度数：

2.例题 在有$n$个顶点的有向图中，每个顶点的度最大可达()。

$A.n$

$B.n-1$

$C.2n$

$D.2n-2$

解：在有向图中，顶点的度等于入度与出度之和。$n$个顶点的有向图中，任意一个顶点最多还可以与其他$n-1$个顶点有一对指向相反的边相连，所以一共$2(n-1)=2n-2$。

生成树与森林：

3.例题 设无向图$G=(V,E)$和$G^{\prime }=(V^{\prime },E^{\prime })$，若$G^{\prime }$是$G$的生成树，则下列说法中错误的是()。

$A.G^{\prime }$为$G$的子图

$B.G^{\prime }$为$G$的连通分量

$C.G^{\prime }$为$G$的极小连通子图且$V=V^{\prime }$

$D.G^{\prime }$是$G$的一个无环子图

解：连通分量是无向图的极大连通子图，其中极大的含义是将依附于连通分量中顶点的所有边都加上，所以连通分量中可能存在回路，这样就不是生成树了。

4.以下叙述中，正确的是()。

$A.$只要无向连通图中没有权值相同的边，则其最小生成树唯一

$B.$只要无向图中有权值相同的边，则其最小生成树一定不唯一

$C.$从$n$个顶点的连通图中选取$n-1$条权值最小的边，即可构成最小生成树

$D.$设连通图$G$含有$n$个顶点，则含有$n$个顶点、$n-1$条边的子图一定是$G$的生成树

解：选项$A$显然正确，图$G$中权值最小的边一定是最小生成树中的边。否则最小生成树加上权值最小的边后构成一个环，去掉环中任意一条非此边则形成了另一个权值更小的生成树。选项$B$，若无向图本身就是一棵树，则最小生成树就是它本身，这时就是唯一的。选项$C$，选取的$n-1$条边可能构成回路。选项$D$，含有$n$个顶点、$n-1$条边的子图可能构成回路，也可能不连通。

邻接表：

5.假设有$n$个顶点、$e$条边的有向图用邻接表表示，则删除与某个顶点$v$相关的所有边的时间复杂度为()。

$A.O(n)$

$B.O(e)$

$C.O(n+e)$

$D.O(ne)$

解：删除与某顶点$v$相关的所有边的过程如下：先删除下标为$v$的顶点表结点的单链表，出边数最多为$n-1$，对应时间复杂度为$O(n)$；再扫描所有边表结点，删除所有的顶点$v$的入边，对应时间复杂度为$O(e)$。故总的时间复杂度为$O(n+e)$。

网络图概念

网络/图形（从技术上讲，网络通常是指真实的系统(网络，社交网络等)，而图形通常是指网络的数学表示形式(网络图，社会图等)。 在这些笔记中，我们将互换使用这些术语。）被定义为对象的集合，其中一些对象对通过链接连接。我们将对象(节点)的集合定义为 $N$, 对象之间的交互(边/链接)定义为 $E$, 将图形定义为 $G(N,E)$。

无向图： 具有对称/双向链接(例如，Facebook上的朋友关系)。我们定义节点度 $k_i$ 为无向图中与节点 $i$ 相邻的边数。那么平均程度是 $$\bar{k}=⟨k⟩=\frac{1}{|N|}\sum _{i=1}^{|N|}{k}_i=\frac{2|E|}{N}$$ 有向图具有定向链接(例如，在Twitter上关注)。我们定义入度 $k_i^{in}$ 为进入节点 $i$ 的边数。同样，我们定义出度 $k_i^{out}$ 为离开节点 $i$ 的边数。 $$\bar{k}=⟨k⟩=\frac{|E|}{N}$$ 完全图，具有最大数量的边的无向图称为完全图(这样所有节点对都被连接)。完全图有 $|E|=\left(\begin{array}{c}N\\ 2\end{array}\right)=\frac{N(N-1)}{2}$ 条边，并且平均度为 $|N|-1$ 。

二分图： 二分图是其节点可以分为两个不相交的集合 $U$ 和 $V$，使得每个边都连接一个集合 $U$ 的节点和一个集合 $V$ 的节点。如果独立集合 $U$ 和 $V$ 共享至少一个共同的邻居，我们可以通过在独立集合中创建边来 “折叠” 二分图。 在这里，如果集合 $U$ 中的节点至少共享一个在 集合 $V$ 中的邻居节点，则集合 $U$ 中的节点将相连形成投影 $U$，采用相同的过程来获得投影 $V$。

networkx画网络图

上一节中，主要解释的是无向图的概念，网络只是一个修饰，并没有实质性的定义，可以结合前面的思维导图中的概念，我们据此调用networkx的api就能直接画出一个简单的无向图：

import networkx as nx
  
edges = [(1, 2), (1, 6), (2, 3), (2, 4), (2, 6), 
         (3, 4), (3, 5), (4, 8), (4, 9), (6, 7)]


G = nx.Graph()    #初始化一个无向图
G.add_edges_from(edges)
nx.draw_networkx(G)
  
print("Total number of nodes: ", int(G.number_of_nodes()))
print("Total number of edges: ", int(G.number_of_edges()))
print("List of all nodes: ", list(G.nodes()))
print("List of all edges: ", list(G.edges(data = True)))
print("Degree for all nodes: ", dict(G.degree()))
print("List of all nodes we can go to in a single step from node 2: ",
                                                 list(G.neighbors(2)))
"""
Total number of nodes:  9
Total number of edges:  10
List of all nodes:  [1, 2, 6, 3, 4, 5, 8, 9, 7]
List of all edges:  [(1, 2, {}), (1, 6, {}), (2, 3, {}), (2, 4, {}), (2, 6, {}), (6, 7, {}), (3, 4, {}), (3, 5, {}), (4, 8, {}), (4, 9, {})]
Degree for all nodes:  {1: 2, 2: 4, 6: 3, 3: 3, 4: 4, 5: 1, 8: 1, 9: 1, 7: 1}
List of all nodes we can go to in a single step from node 2:  [1, 3, 4, 6]

"""

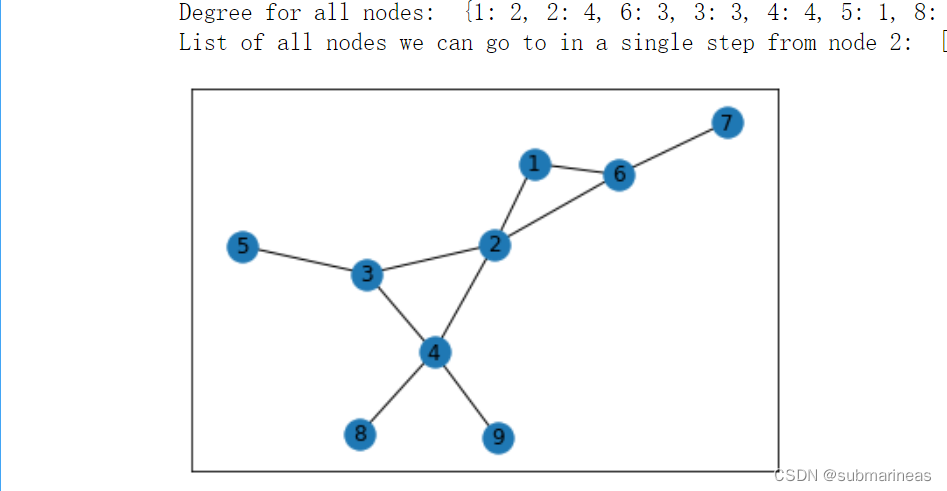
画出无向图后，我们还可以在这个的基础上进行加权，画加权无向图，为：

import networkx as nx
G = nx.Graph()
  
edges = [(1, 2, 19), (1, 6, 15), (2, 3, 6), (2, 4, 10), 
         (2, 6, 22), (3, 4, 51), (3, 5, 14), (4, 8, 20),
         (4, 9, 42), (6, 7, 30)]
  
G.add_weighted_edges_from(edges)
nx.draw_networkx(G, with_labels = True)

我们发现上述图形都是没有方向的，即两个相连的顶点可以互相抵达。而有向图的边是有方向的，即两个相连的顶点，根据边的方向，只能由一个顶点通向另一个顶点。即继续画出有向图为：

Total number of nodes:  9
Total number of edges:  15
List of all nodes:  [1, 7, 2, 3, 6, 5, 4, 8, 9]
List of all edges:  [(1, 1), (1, 7), (7, 2), (7, 6), (2, 1), (2, 2), (2, 3), (2, 6), (3, 5), (6, 4), (5, 4), (5, 8), (5, 9), (4, 3), (8, 7)]
In-degree for all nodes:  {
    
    1: 2, 7: 2, 2: 2, 3: 2, 6: 2, 5: 1, 4: 2, 8: 1, 9: 1}
Out degree for all nodes:  {
    
    1: 2, 7: 2, 2: 4, 3: 1, 6: 1, 5: 3, 4: 1, 8: 1, 9: 0}
List of all nodes we can go to in a single step from node 2:  [1, 2, 3, 6]
List of all nodes from which we can go to node 2 in a single step:  [2, 7]

我们还可以将上述构建节点的权重写进txt文件，通过read_edgelist读出：

import networkx as nx
alist = [(1, 2, 19), (1, 6, 15), (2, 3, 6), (2, 4, 10),
         (2, 6, 22), (3, 4, 51), (3, 5, 14), (4, 8, 20),
         (4, 9, 42), (6, 7, 30)]
with open("data.txt", 'w') as f:
    for i in alist:
        # print(list(i),"..........i")
        f.write(' '.join(str(x) for x in i) + '\n')

G = nx.read_edgelist('edge_list.txt', data =[('Weight', int)])
print(G)
"""
Graph with 9 nodes and 10 edges
"""

我们可以根据该data.txt中的数据直接画出跟上面一致的网络图，这里不再演示，切换成另一数据集，即印度各个城市的人口以及它们之间的距离数据集：

Kolkata Mumbai 2031
Mumbai Pune 155
Mumbai Goa 571
Kolkata Delhi 1492
Kolkata Bhubaneshwar 444
Mumbai Delhi 1424
Delhi Chandigarh 243
Delhi Surat 1208
Kolkata Hyderabad 1495
Hyderabad Chennai 626
Chennai Thiruvananthapuram 773
Thiruvananthapuram Hyderabad 1299
Kolkata Varanasi 679
Delhi Varanasi 821
Mumbai Bangalore 984
Chennai Bangalore 347
Hyderabad Bangalore 575
Kolkata Guwahati 1031

直接替换data.txt 中的内容，或者也能尝试跟我上面那样，我上面写文件的代码只是我写得一个模拟，如果要还原成元组或者列表的形式，可以在换行符和空格这两个做文章，切回正题，文件生成后，加入各城市的人口数据，画出图为：

import networkx as nx
  
G = nx.read_weighted_edgelist('data.txt', delimiter =" ")
  
population = {
    
    
        'Kolkata' : 4486679,
        'Delhi' : 11007835,
        'Mumbai' : 12442373,
        'Guwahati' : 957352,
        'Bangalore' : 8436675,
        'Pune' : 3124458,
        'Hyderabad' : 6809970,
        'Chennai' : 4681087,
        'Thiruvananthapuram' : 460468,
        'Bhubaneshwar' : 837737,
        'Varanasi' : 1198491,
        'Surat' : 4467797,
        'Goa' : 40017,
        'Chandigarh' : 961587
        }
  
for i in list(G.nodes()):
    G.nodes[i]['population'] = population[i]
  
nx.draw_networkx(G, with_label = True)

但这里发现一个问题，就是我们的数据在图中并没有表现出更为具体的信息，按照正常来讲，应该有的是：

1. 节点的大小与城市的人口成正比。
2. 节点颜色的深浅与节点的度数成正比。
3. 边的宽度与边的权重成正比，在这种情况下，就是城市之间的距离。

所以，稍微处理一下这些关系，得到的图表为：

# fixing the size of the figure
plt.figure(figsize =(10, 7))
  
node_color = [G.degree(v) for v in G]
  
node_size = [0.0005 * nx.get_node_attributes(G, 'population')[v] for v in G]
  
edge_width = [0.0015 * G[u][v]['weight'] for u, v in G.edges()]
  
nx.draw_networkx(G, node_size = node_size, 
                 node_color = node_color, alpha = 0.7,
                 with_labels = True, width = edge_width,
                 edge_color ='.4', cmap = plt.cm.Blues)
  
plt.axis('off')
plt.tight_layout();

到此，networkx的一些基本功能与社交网络的一些属性可视化到此为止。

图补充

最短路径

• 单源最短路径：单个顶点到图的其他顶点的最短路径。

  • $BFS$算法（无权图）。
  • $Dijkstra$ 算法（带权图、无权图）。

• 每对顶点间最短路径：每对顶点之间的最短路径。

  • $Floyd$算法（带权图、无权图）。

最短路径一定是简单路径（不存在环）。但是无论有没有环的有向图与是否存在最短路径无关。

$Dijkstra$ 算法伪代码：

void Dijkstra(){
    
    
	for(i=0;i<n-1;++i){
    
    
		min=INF;
		index=0;
		for(j=0;j<n;++j){
    
    
			if(!visited[j] && dis[j]<min){
    
    
				min=dis[j];
				index=j;
			}
		}
		visited[index]=true;
		for(j=0;j<n;++j){
    
    
			if(!visited[j] && edge[index][j]<INF){
    
    
				dis[j]=min(dis[j],dis[index]+edge[index][j]);
			}
		}
	}
}

$Floyd$ 算法伪代码：

void Floyd(){
    
    
	for(k=0;k<n;++k){
    
    
		for(i=0;i<n;++i){
    
    
			for(j=0;j<n;++j){
    
    
				dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
			}
		}
	}
}

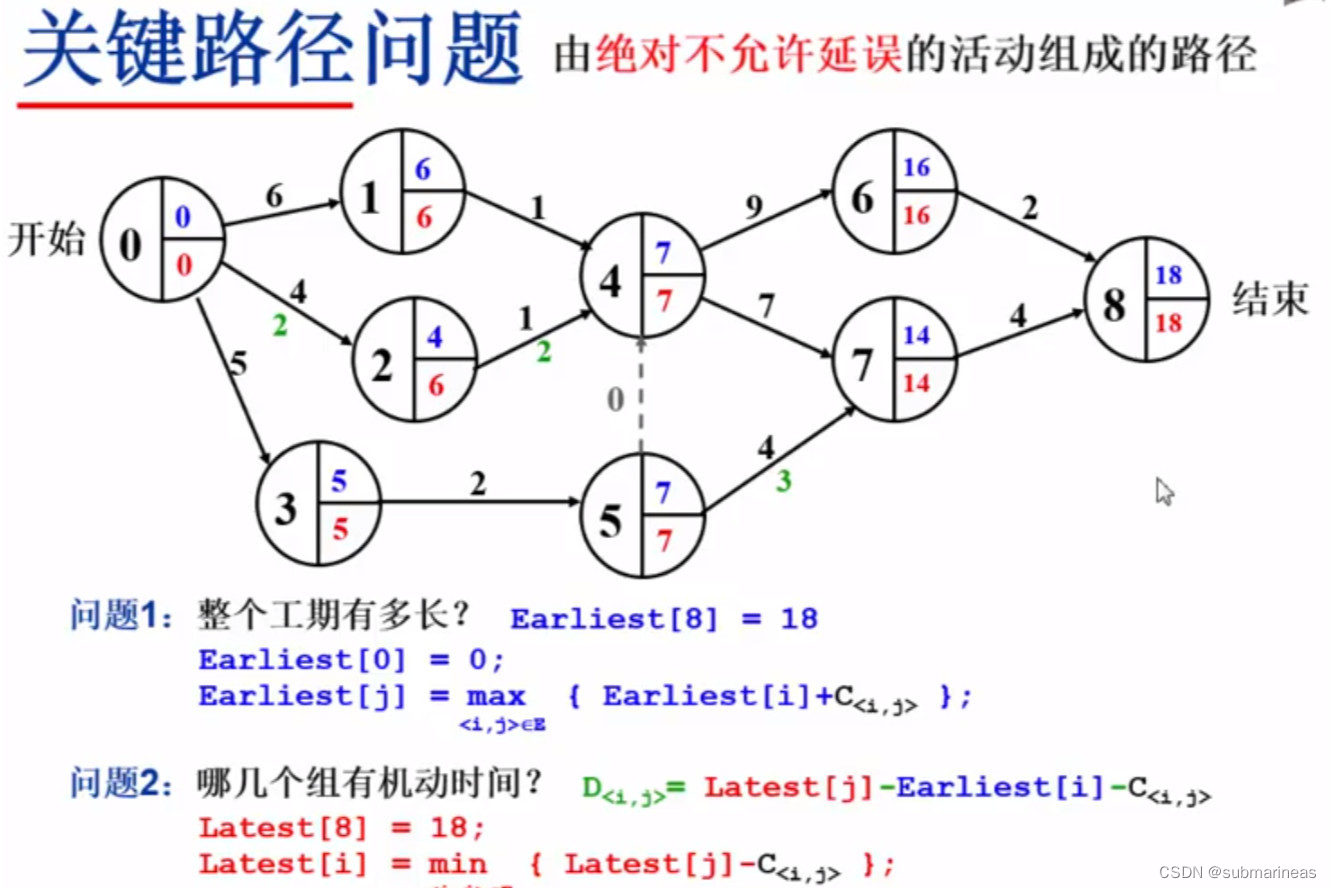
关键路径

在带权有向图中，以顶点表示时间，以有向边表示活动，以边上的权值表示完成该活动的开销，称之为用边表示活动的网络，简称$AOE$网。

• 只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始。
• 只有在进入某顶点的各有向边所代表的活动都已经结束时，该顶点所代表的事件才能发生，活动也可以并行进行。
• 只有一个入度为$0$的顶点，即开始顶点（源点），表示整个工程的开始。
• 只有一个出度为$0$的顶点，称为结束顶点（汇点），表示整个工程的结束。
• 从源点到汇点的有向路径可能有多条，所有路径中，具有最大路径长度的路径称为关键路径（即决定完成整个工程所需的最小时间），而关键路径上的活动称为关键活动。
• 事件的最早发生时间：决定了所有从该事件开始的活动能够开工的最早时间。一个事件的最早发生时间与以该事件为始的弧的活动的最早开始时间相同。
• 活动的最早开始时间：指该活动弧的起点所表示的事件最早发生时间。
• 事件的最迟发生时间：在不推迟整个工程完成的前提下，该事件最迟必须发生的时间。一个事件的最迟发生时间等于$\min${以该事件为尾的弧的活动的最迟开始时间，最迟结束时间与该活动的持续时间的差}。
• 活动的最迟开始时间：指该活动弧的终点所表示的事件的最迟发生时间与该活动所需时间之差。
• 活动的时间余量：在不增加完成整个工程所需总时间的情况下，活动可以拖延的时间。

参考与推荐

[1]. stanfold 224w官方主页：CS224W: Machine Learning with Graphs

[2]. stanfold官方笔记：https://snap-stanford.github.io/cs224w-notes/

[3]. cs224w（图机器学习）2021冬季课程学习笔记集合

[4]. 同济子豪兄：斯坦福CS224W图机器学习

[5]. https://github.com/TommyZihao/zihao_course

[6]. 王道2023——数据结构

[7]. Directed Graphs, Multigraphs and Visualization in Networkx

[8]. 最短路径算法

[9]. Dijkstra算法和Floyd算法超详解以及区别

[10]. 关键路径法