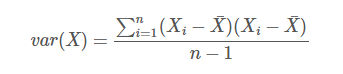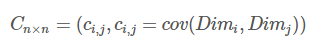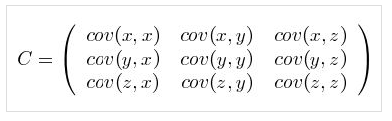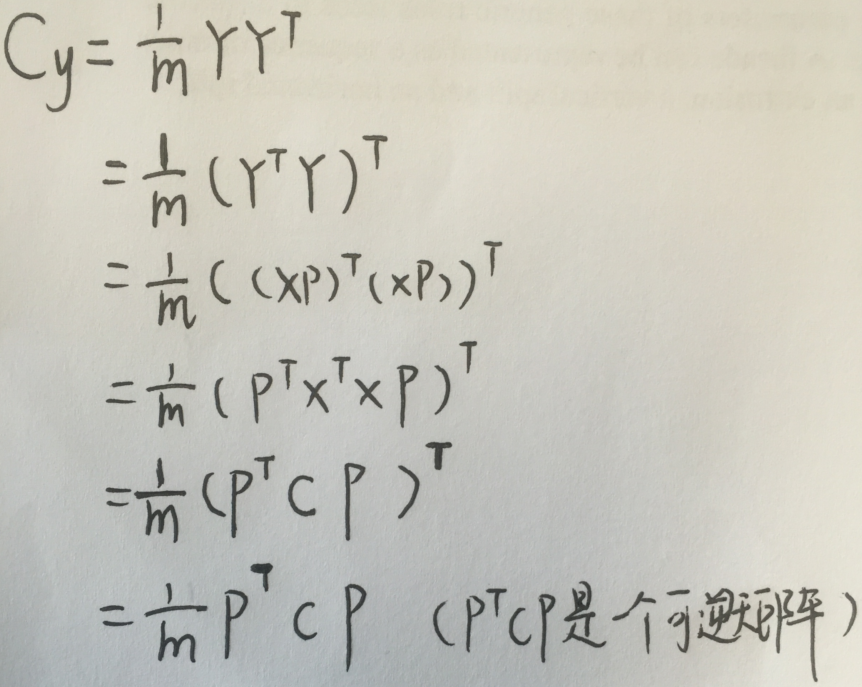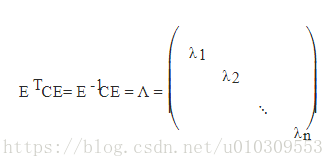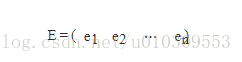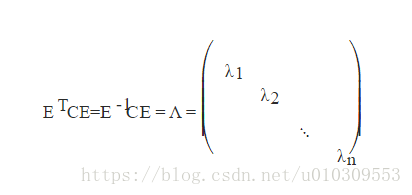一、协方差矩阵
一个维度上方差的定义:
协方差的定义:
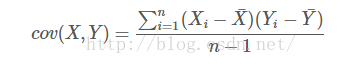
协方差就是计算了两个维度之间的相关性,即这个样本的这两个维度之间有没有关系。
协方差为0,证明这两个维度之间没有关系,协方差为正,两个正相关,为负则负相关。
协方差矩阵的定义:
对n个维度,任意两个维度都计算一个协方差,组成矩阵,定义如下
直观的对于一个含有x,y,z三个维度的样本,协方差矩阵如下
可以看出,对角线表示了样本在在各个维度上的方差。
其他元素表示了不同维度之间两两的关联关系。
二、协方差矩阵的计算
(1)先让样本矩阵中心化,即每一维度减去该维度的均值,使每一维度上的均值为0,
(2)然后直接用新的到的样本矩阵乘上它的转置
(3)然后除以(N-1)即可‘
数学推导相对容易,样本矩阵中心化以后,样本均值为0,因此式a中每个维度无需减去均值,只需要进行与其他维度的乘法,
这样就可以用转置相乘实现任意两两维度的相乘。
三、矩阵相乘的“变换的本质”理解
A*B两个矩阵相乘代表什么?
A的每一行所表示的向量,变到B的所有列向量为基底表示的空间中去,得到的每一行的新的表示。
B的每一列所表示的向量,变到A的所有行向量为基底表示的空间中去,得到的每一列的新的表示。
三、PCA深入
PCA的目的是降噪和去冗余,是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维。
样本矩阵的格式:
样本1 [特征a1,特征a2,特征a3,…..,特征an]
样本2 [特征a1,特征a2,特征a3,…..,特征an]
样本3 [特征a1,特征a2,特征a3,…..,特征an]
样本4 [特征a1,特征a2,特征a3,…..,特征an]
PCA后:r<n
样本1 [特征b1,特征b2,特征b3,…..,特征br]
样本2 [特征b1,特征b2,特征b3,…..,特征br]
样本3 [特征b1,特征b2,特征b3,…..,特征br]
样本4 [特征b1,特征b2,特征b3,…..,特征br]
直白的来说,就是对一个样本矩阵,
(1)换特征,找一组新的特征来重新表示
(2)减少特征,新特征的数目要远小于原特征的数目
我们来看矩阵相乘的本质,用新的基底去表示老向量,这不就是重新找一组特征来表示老样本吗???
所以我们的目的是什么?就是找一个新的矩阵(也就是一组基底的合集),让样本矩阵乘以这个矩阵,实现换特征+减少特征的重新表示。
因此我们进行PCA的基本要求是:
(1)第一个要求:使得样本在选择的基底上尽可能的而分散。
为什么这样?
极限法,如果在这个基底上不分散,干脆就在这个基地上的投影(也就是特征)是一样的。那么会有什么情况?
想象一个二维例子:
以下这一组样本,有5个样本,有2个特征x和y,矩阵是
[-1,-2]
[-1, 0]
[ 0, 0]
[ 2, 1]
[ 0, 1]
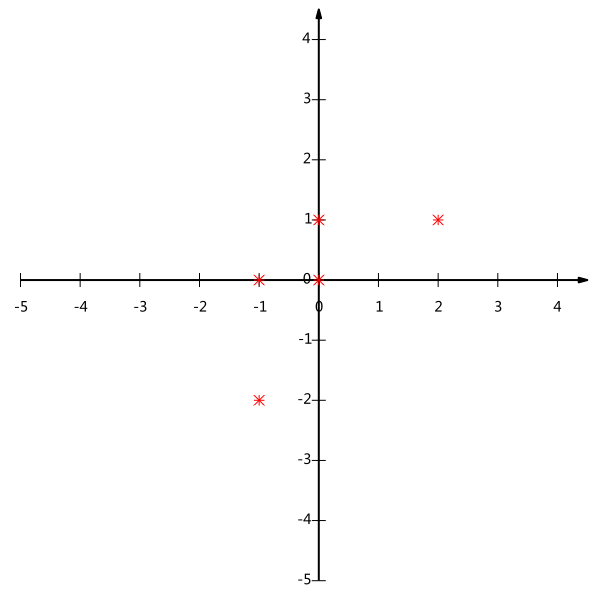
画图如下:
我现在是二维特征表示,x一个特征,y一个特征。我现在降维。
降成一维,我要选一个新的基底(特征)。
如果我选(1,0)作为基底,就是x轴嘛,然后我把这些样本投影到x轴,或者乘以[1,0]列向量。
得,里面好几个数都一样,分不出来了。
所以这就是为样本在基底上要尽可能分散了,这个分散不就是样本在这个“基底上的坐标”(这个基底上的特征值)的方差要尽可能大么?
(2)第二个要求:使得各个选择的基底关联程度最小。
刚才是二维降一维,只选则一个一维基底就可以了,太拿衣服了。
考虑一个三维点投影到二维平面的例子。这样需要俩基底。
基底得一个一个找啊,先找第一个,要找一个方向,使得样本在这个方向上方差最大。
再找第二个基底,怎么找,方差最大?这不还是找的方向和第一个差不多么?那这两个方向表示的信息几乎是重复的。
所以从直观上说,让两个字段尽可能表示更多的原始信息,我们是不希望它们之间存在(线性)相关性的,因为相关性意味着两个字段不是完全独立,必然存在重复表示的信息。所以最好就是选择和第一个基底正交的基底。
那怎么找呢?不能随便写一个矩阵吧?答案肯定是要基于原来的样本的表示。
我们求出了原来样本的协方差矩阵,协方差矩阵的对角线代表了原来样本在各个维度上的方差,其他元素代表了各个维度之间的相关关系。
也就是说我们希望优化后的样本矩阵,它的协方差矩阵,对角线上的值都很大,而对角线以外的元素都为0。
现在我们假设这个样本矩阵为X(每行对应一个样本),X对应的协方差矩阵为Cx,而P是我们找到的对样本进行PCA变换的矩阵,即一组基按列组成的矩阵,我们有Y=XP
Y即为我们变化后的新的样本表示矩阵,我们设Y的协方差矩阵维Cy,我们想让协方差矩阵Cy是一个对角阵,那么我们先来看看Cy的表示
注意:
推导规程为了把X凑一起,我们用了Y Yt=((Y Yt)t)t=(Yt Y)t
把样本组织成行向量和列向量是一样的原来,最后结果只需要一个转置就变成一个格式了。把样本X组织成列向量,就要把基底P组织成行向量,就要写PX了
好了,我们退出了Cy的表示,最后的结果很神奇的成了一个熟悉的形式:方阵可对角化的表达式
让我们来回忆一下可对角化矩阵的定义,顺便也回忆了矩阵相似的定义:
(1)什么是可对角化和相似:如果一个方块矩阵 A 相似于对角矩阵,也就是说,如果存在一个可逆矩阵 P 使得 P −1AP 是对角矩阵,则它就被称为可对角化的。
(2)如何判断可对角化呢:我们再来回忆一下矩阵可对角化的条件:n × n 矩阵 A 只在域 F 上可对角化的,如果它在 F 中有 n 个不同的特征值,就是说,如果它的特征多项式在 F 中有 n 个不同的根,也就说他有n个线性无关的特征向量,这三条件是等价的,满足一个就可以对角化。
注意哦:有n个线性无关的特征向量并不一定代表有n个不同的特征值,因为可能多个特征向量的对于空间的权重相同嘛。。。但是n个不同的特征值一定有n个线性无关的特征向量啦。
C是啥呢,C是协方差矩阵,协方差矩阵是实对称矩阵,就是实数的意思,有很多很有用的性质
1)实对称矩阵不同特征值对应的特征向量,不仅是线性无关的,还是正交的。
2)设特征向量重数为r,则必然存在r个线性无关的特征向量对应于,因此可以将这r个特征向量单位正交化。
3) n阶实对称矩阵C,一定存在一个正交矩阵E,满足如下式子,即C既相似又合同于对角矩阵。(这里又温习了合同的概念哦)
由上面两条可知,一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量,设这n个特征向量为e1,e2,…,en
我们将其按列组成矩阵:
则对协方差矩阵C有如下结论:
PCA算法步骤总结:
设有m条n维数据,这里比较糊涂就是按行组织样本还是按列组织样本,下面是按行组织样本:
1)将原始数据按行组成n行m列矩阵X,代表有n个数据,每个数据m个特征
2)将X的每一列(代表一个属性字段)进行零均值化,即减去这一列的均值
3)求出协方差矩阵C=1/n* XXT
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按列排列成矩阵,取前k列组成矩阵P
6)Y=XP即为降维到k维后的数据
按列组织是这样的,理解一下:
1)将原始数据按列组成n行m列矩阵X
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵C=1/m*XXT
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6)Y=PX即为降维到k维后的数据
</div>
一、协方差矩阵
一个维度上方差的定义:
协方差的定义:
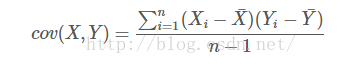
协方差就是计算了两个维度之间的相关性,即这个样本的这两个维度之间有没有关系。
协方差为0,证明这两个维度之间没有关系,协方差为正,两个正相关,为负则负相关。
协方差矩阵的定义:
对n个维度,任意两个维度都计算一个协方差,组成矩阵,定义如下
直观的对于一个含有x,y,z三个维度的样本,协方差矩阵如下
可以看出,对角线表示了样本在在各个维度上的方差。
其他元素表示了不同维度之间两两的关联关系。
二、协方差矩阵的计算
(1)先让样本矩阵中心化,即每一维度减去该维度的均值,使每一维度上的均值为0,
(2)然后直接用新的到的样本矩阵乘上它的转置
(3)然后除以(N-1)即可‘
数学推导相对容易,样本矩阵中心化以后,样本均值为0,因此式a中每个维度无需减去均值,只需要进行与其他维度的乘法,
这样就可以用转置相乘实现任意两两维度的相乘。
三、矩阵相乘的“变换的本质”理解
A*B两个矩阵相乘代表什么?
A的每一行所表示的向量,变到B的所有列向量为基底表示的空间中去,得到的每一行的新的表示。
B的每一列所表示的向量,变到A的所有行向量为基底表示的空间中去,得到的每一列的新的表示。
三、PCA深入
PCA的目的是降噪和去冗余,是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维。
样本矩阵的格式:
样本1 [特征a1,特征a2,特征a3,…..,特征an]
样本2 [特征a1,特征a2,特征a3,…..,特征an]
样本3 [特征a1,特征a2,特征a3,…..,特征an]
样本4 [特征a1,特征a2,特征a3,…..,特征an]
PCA后:r<n
样本1 [特征b1,特征b2,特征b3,…..,特征br]
样本2 [特征b1,特征b2,特征b3,…..,特征br]
样本3 [特征b1,特征b2,特征b3,…..,特征br]
样本4 [特征b1,特征b2,特征b3,…..,特征br]
直白的来说,就是对一个样本矩阵,
(1)换特征,找一组新的特征来重新表示
(2)减少特征,新特征的数目要远小于原特征的数目
我们来看矩阵相乘的本质,用新的基底去表示老向量,这不就是重新找一组特征来表示老样本吗???
所以我们的目的是什么?就是找一个新的矩阵(也就是一组基底的合集),让样本矩阵乘以这个矩阵,实现换特征+减少特征的重新表示。
因此我们进行PCA的基本要求是:
(1)第一个要求:使得样本在选择的基底上尽可能的而分散。
为什么这样?
极限法,如果在这个基底上不分散,干脆就在这个基地上的投影(也就是特征)是一样的。那么会有什么情况?
想象一个二维例子:
以下这一组样本,有5个样本,有2个特征x和y,矩阵是
[-1,-2]
[-1, 0]
[ 0, 0]
[ 2, 1]
[ 0, 1]
画图如下:
我现在是二维特征表示,x一个特征,y一个特征。我现在降维。
降成一维,我要选一个新的基底(特征)。
如果我选(1,0)作为基底,就是x轴嘛,然后我把这些样本投影到x轴,或者乘以[1,0]列向量。
得,里面好几个数都一样,分不出来了。
所以这就是为样本在基底上要尽可能分散了,这个分散不就是样本在这个“基底上的坐标”(这个基底上的特征值)的方差要尽可能大么?
(2)第二个要求:使得各个选择的基底关联程度最小。
刚才是二维降一维,只选则一个一维基底就可以了,太拿衣服了。
考虑一个三维点投影到二维平面的例子。这样需要俩基底。
基底得一个一个找啊,先找第一个,要找一个方向,使得样本在这个方向上方差最大。
再找第二个基底,怎么找,方差最大?这不还是找的方向和第一个差不多么?那这两个方向表示的信息几乎是重复的。
所以从直观上说,让两个字段尽可能表示更多的原始信息,我们是不希望它们之间存在(线性)相关性的,因为相关性意味着两个字段不是完全独立,必然存在重复表示的信息。所以最好就是选择和第一个基底正交的基底。
那怎么找呢?不能随便写一个矩阵吧?答案肯定是要基于原来的样本的表示。
我们求出了原来样本的协方差矩阵,协方差矩阵的对角线代表了原来样本在各个维度上的方差,其他元素代表了各个维度之间的相关关系。
也就是说我们希望优化后的样本矩阵,它的协方差矩阵,对角线上的值都很大,而对角线以外的元素都为0。
现在我们假设这个样本矩阵为X(每行对应一个样本),X对应的协方差矩阵为Cx,而P是我们找到的对样本进行PCA变换的矩阵,即一组基按列组成的矩阵,我们有Y=XP
Y即为我们变化后的新的样本表示矩阵,我们设Y的协方差矩阵维Cy,我们想让协方差矩阵Cy是一个对角阵,那么我们先来看看Cy的表示
注意:
推导规程为了把X凑一起,我们用了Y Yt=((Y Yt)t)t=(Yt Y)t
把样本组织成行向量和列向量是一样的原来,最后结果只需要一个转置就变成一个格式了。把样本X组织成列向量,就要把基底P组织成行向量,就要写PX了
好了,我们退出了Cy的表示,最后的结果很神奇的成了一个熟悉的形式:方阵可对角化的表达式
让我们来回忆一下可对角化矩阵的定义,顺便也回忆了矩阵相似的定义:
(1)什么是可对角化和相似:如果一个方块矩阵 A 相似于对角矩阵,也就是说,如果存在一个可逆矩阵 P 使得 P −1AP 是对角矩阵,则它就被称为可对角化的。
(2)如何判断可对角化呢:我们再来回忆一下矩阵可对角化的条件:n × n 矩阵 A 只在域 F 上可对角化的,如果它在 F 中有 n 个不同的特征值,就是说,如果它的特征多项式在 F 中有 n 个不同的根,也就说他有n个线性无关的特征向量,这三条件是等价的,满足一个就可以对角化。
注意哦:有n个线性无关的特征向量并不一定代表有n个不同的特征值,因为可能多个特征向量的对于空间的权重相同嘛。。。但是n个不同的特征值一定有n个线性无关的特征向量啦。
C是啥呢,C是协方差矩阵,协方差矩阵是实对称矩阵,就是实数的意思,有很多很有用的性质
1)实对称矩阵不同特征值对应的特征向量,不仅是线性无关的,还是正交的。
2)设特征向量重数为r,则必然存在r个线性无关的特征向量对应于,因此可以将这r个特征向量单位正交化。
3) n阶实对称矩阵C,一定存在一个正交矩阵E,满足如下式子,即C既相似又合同于对角矩阵。(这里又温习了合同的概念哦)
由上面两条可知,一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量,设这n个特征向量为e1,e2,…,en
我们将其按列组成矩阵:
则对协方差矩阵C有如下结论:
PCA算法步骤总结:
设有m条n维数据,这里比较糊涂就是按行组织样本还是按列组织样本,下面是按行组织样本:
1)将原始数据按行组成n行m列矩阵X,代表有n个数据,每个数据m个特征
2)将X的每一列(代表一个属性字段)进行零均值化,即减去这一列的均值
3)求出协方差矩阵C=1/n* XXT
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按列排列成矩阵,取前k列组成矩阵P
6)Y=XP即为降维到k维后的数据
按列组织是这样的,理解一下:
1)将原始数据按列组成n行m列矩阵X
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵C=1/m*XXT
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6)Y=PX即为降维到k维后的数据
</div>