协方差->相关系数->协方差矩阵->PCA

协方差

定义

$Cov(X, Y)=\frac{\sum_{i=1}^{n}(X_i-\mu_x)(Y_i-\mu_y)}{n}$

向量形式： $Cov(X, Y)=\frac{(\vec x-\mu_x)^T(\vec y-\mu_y)}{n}$

无偏统计量

向量形式： $Cov(X, Y)=\frac{(\vec x-\bar x)^T(\vec y-\bar y)}{n-1}$

协方差Cov(X, Y)的意义

• 如果两个变量的变化趋势一致（若观察到X大于自身的期望值时，同时观察到Y大于自身的期望值），那么两个变量之间的协方差就是正值
• 如果两个变量的变化趋势相反（若观察到X大于自身的期望值时，同时观察到Y小于自身的期望值），那么两个变量之间的协方差就是负值
• 如果两个变量不相关（若观察到X大于自身的期望值时，同时观察到Y仍为自身的期望值），那么两个变量之间的协方差就是0

不相关却不独立的例子

我们来理一下逻辑，如果我们从样本点的分布，推断出相关关系，那么一定意味者这两个变量一定不独立，这个因素才会导致我们观察到相关关系。我们能直接看出来的只有线性关系。

但我们如果观察不到相关关系，并不意味这两个变量内在没有联系。

反例如下:

(x, y) 均匀分布在单位元 $x^2+y^2=1$上，我们是看不出(x, y)有线性关系的，证明一下：
$E_{XY}(XY)=E_X(E_Y(Y|X))=E_Y(E_X(X|Y))=0$
$Cov(XY)=E(XY)-E(X)E(Y)=0$

总结

• 协方差表征的是两个随机变量间的线性关系，称为相关关系
• 独立一定不相关，不相关不一定独立。 $Cov(X, Y)=E[XY]-E[X]E[Y]=E[X][Y](X, Y相互独立时)-E[X][Y]=0$
• 对于均值为零的高斯随机变量，“独立”和“不相关”等价的
• 协方差的具体取值
  • Cov(X, Y) > 0，样本分布的X, Y变化的方向相同
  • Cov(X, Y) < 0，样本分布的X, Y变化的方向相反
  • Cov(X, Y) = 0，样本分布的X, Y变化的方向无关

相关系数

为了能准确地研究两个变量在变化过程中的相似程度，我们就要把变化幅度对协方差的影响从协方差中剔除掉，得到相关系数：

$r=\frac{Cov(X, Y)}{\sigma_X\sigma_Y}$
向量形式： $r=\frac{(\vec x-\bar x)^T(\vec y-\bar y)}{||\vec x-\bar x||||\vec y-\bar y||}$

相关系数与余弦距离的关系

r其实就是样本序列X: $(x_1, x_2, x_i, ...)$和Y: $(y_1, y_2, y_i, ...)$归一化后的余弦距离。

如，X的样本(-1, 1)和Y的样本(-2, 2)时，r=1；可见r捕捉的时不同随机变量之间的线性趋同性。

性质

• $|r|\le1$
• $|r|=1$的充要条件是存在常数a, b，使得 $P\{Y=a+bX\}=1$

协方差矩阵

设 $X$为 $[\vec{x_1}, \vec{x_2},...]$（其中 $\vec{x_i}$为所有样本的第i维组成的列向量）, $\mu$为 $[\mu_1, \mu_2, ...]$

协方差矩阵 $\sum=\frac{(X-\mu)^T(X-\mu)}{n}$

PCA

对X进行线性变换，则 $Y=XU$（ $U_i$为U的第i列，表征怎么从旧坐标整合出新坐标的第i维度）

此时，Y的协方差矩阵为
$\sum_Y=\frac{(Y-\mu U)^T(Y-\mu U)}{n}=\frac{(XU-\mu U)^T(XU-\mu U)}{n}=U^T\sum_XU$

对于新坐标下的第i维和第j维有如下关系，

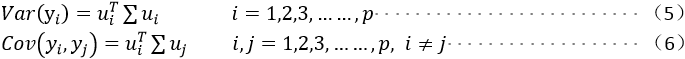
我们想找到的主成分 $max(\sum_Y(1, 1))$，即

根据线性代数的知识可以知道，u应该取 $\sum_X$得最大特征值对应得特征向量。