目录
| Table of Contents |
| - 一.递推最小二乘法(RLS)算法 - 1.1 以N阶线性系统起点, - 1.2 动机: - 1.3 目标函数的定义: - 1.3.1 基于指数加权定义目标函数: - 1.3.2 后验与先验误差对比: - 1.3.2 最小化目标函数J(w): - 1.4 求解滤波器系数 - 1.4.1 推导自相关矩阵和相关向量的时间递推公式: - 1.4.2 自相关矩阵时间递推公式的优化: - 矩阵求逆引理: - R逆的时间递推公式: - 1.4.3 滤波器系数w(n)的时间递推公式: - 1.5 RLS算法的执行流程: - 1.6 RLS vs LMS |
一.递推最小二乘法(RLS)算法
1.1 以N阶线性系统起点,


1.2 动机:
MMSE是一个均匀加权的最优化问题,即每一个时刻的误差信号对目标函数的贡献一样
对于非平稳信号,需要调整目标函数的定义方式,使得越近的时刻误差贡献越大,越远时刻误差贡献越小。
1.3 目标函数的定义:
1.3.1 基于指数加权定义目标函数:

4.1,其实就是均方误差再乘一个步长的指数因子,调节不同时刻的误差大小。
指数函数对应形式y = a^x , 且a(这里那么大)属于(0,1],函数单调递减, 又因为 n-i >=0, 当i越接近n时,n-i越趋近于0,所以值越大,即误差权重越大。
1.3.2 后验与先验误差对比:

这里使用后验误差结果比使用先验误差小,先验和后验实际应用结果有时差别不大,但理论上存在较大差异。
1.3.2 最小化目标函数J(w):

R物理含义是一个加权的相关矩阵的求和。包含了从0时刻到n时刻所有输入向量取相关矩阵。
1.4 求解滤波器系数
1.4.1 推导自相关矩阵和相关向量的时间递推公式:

4.3,可以经过简单的拆项推导可以得出4.5,发现n时刻可以由n-1时刻推出。4.6的得来同理。 所以理论上可以直接经过递推得到R的逆 和r,然后计算出n时刻的 w(n)。
但逆矩阵的存在会导致数值不稳定的风险,所以这里R需要另外再找方法进行推导。
1.4.2 自相关矩阵时间递推公式的优化:
(避开求R逆的逆矩阵)
矩阵求逆引理:
R逆的时间递推公式:

矩阵求逆引理,标量和向量都可以应用。
先验估计误差:
1.4.3 滤波器系数w(n)的时间递推公式:

最终的结果表示,w(n)是由w(n-1)加上一个调整量。 调整量中k(n)是增益向量。瑟塔是先验误差,通过对前一时刻w(n-1)计算得来,所有称之为先验估计误差。
这里先验误差和上一节LMS采用的后验误差有差别,并且维纳滤波也是采用的后验误差。
1.5 RLS算法的执行流程:

如上图1)中, P(0)表示相关矩阵R逆(0),由于相关矩阵可以表示成如上红色笔求和公式。 又因为希望当更新第n时刻的滤波器系数时,时间越远影响越小,所以由输入向量 x 计算的相关矩阵初始值设定为接近0的单位矩阵。
为了计算方便每次计算都对逆矩阵进行更新。
1.6 RLS vs LMS
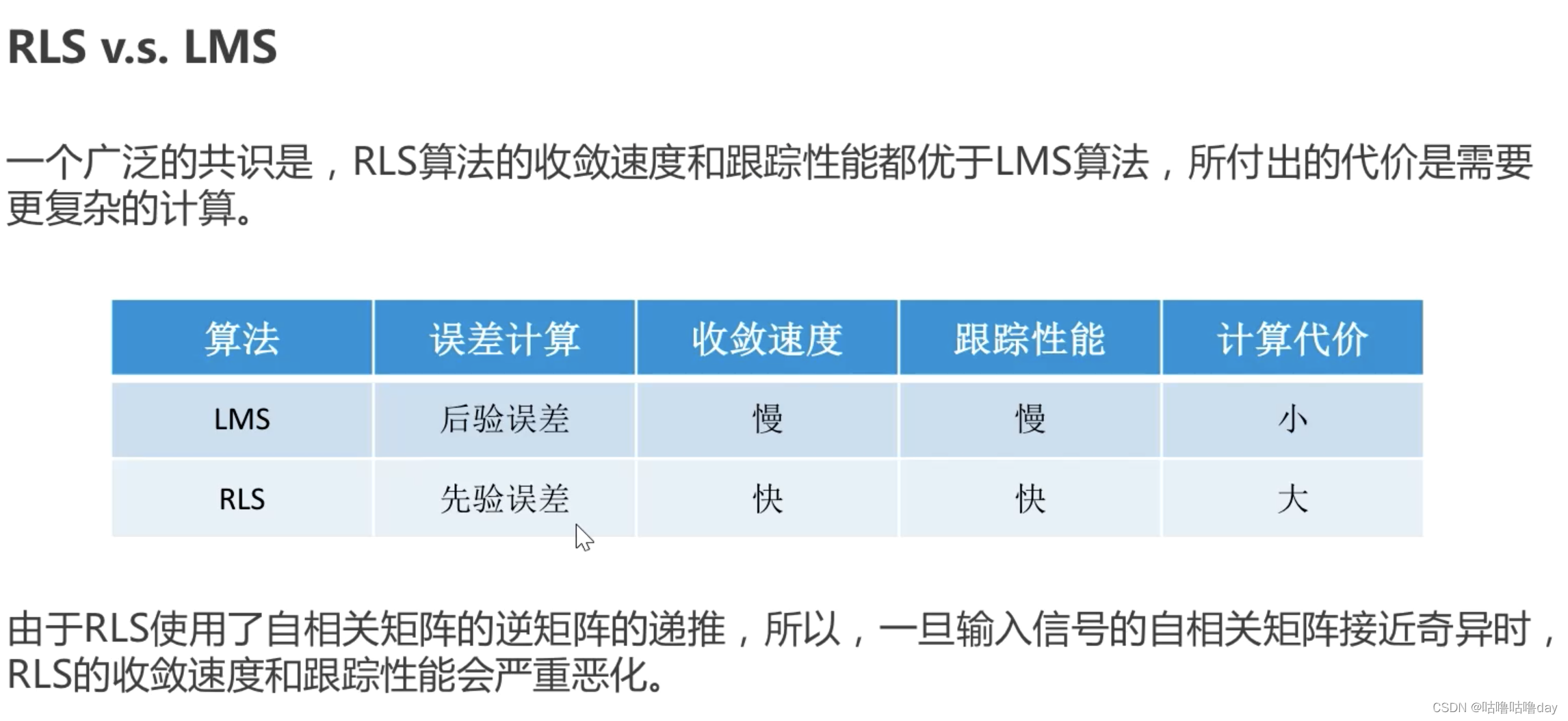
LMS对输入信号也隐含一个条件,即希望输入信号是具有独立性假设,即各个时刻的输入信号尽量不相关,太相关则会导致相关矩阵接近奇异矩阵。与LMS对输入信号的要求一样。