Threshold ECDSA

分为分布式密钥生成和签名，核心内容来自GG18的主要逻辑部分。

ECC

椭圆曲线密码学，基于有限域的椭圆曲线和椭圆曲线离散对数，非对称，私钥为一个整数，公钥为椭圆曲线上的点。

基本概念

椭圆曲线

概念
二元三次方程
最常用的表达式为 { ( x , y ) ∈ R 2 ∣ y 2 = x 3 + a x + b , 4 a 3 + 27 b 2 ≠ 0 } ∪ { 0 } \left\{(x, y) \in \mathbb{R}^{2} \mid y^{2}=x^{3}+a x+b, 4 a^{3}+27 b^{2} \neq 0\right\} \cup\{0\} { (x,y)∈R2∣y2=x3+ax+b,4a3+27b2=0}∪{ 0}，右边为一个无穷远的点，用O或者0这个符号表示。左边括号里面右边的条件是为了保证曲线不含奇点（无极限，无定义）
大概长这样，如图

椭圆曲线上的群论
为了建立曲线上点与点之间的联系，在椭圆曲线上定义阿贝尔群（封闭，结合，单位元，逆元，交换）：

• 群中元素为曲线上点，
• 单位元为无穷处的点，
• 逆元为关于x轴的对称点，
• 加法定义为点加，取一条直线与椭圆曲线相交的非零三点P，Q，R，满足$P+Q+R=0，P+Q=-R$

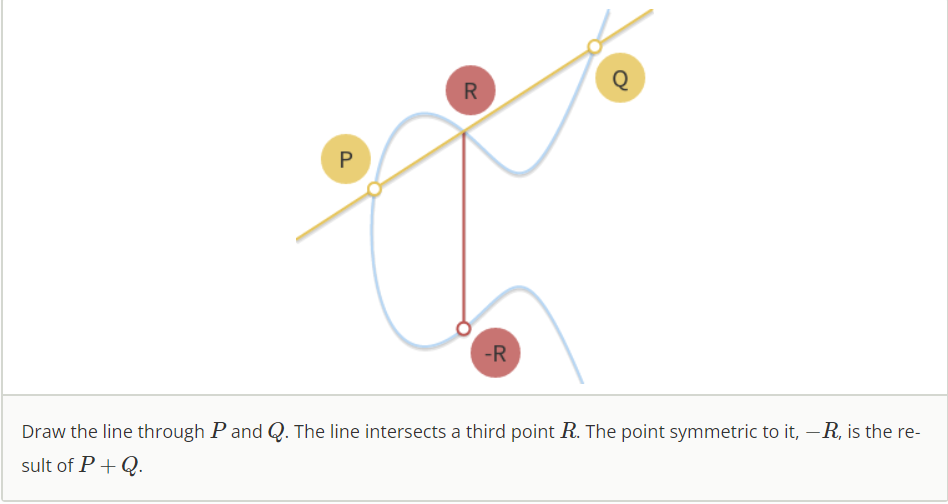
加法
椭圆曲线上的计算主要为点加法，也就是已知两点求另外一点，几何法可以直接画图，代数法如下，
考虑P，Q非零，求得R得方法为

1. 求得斜率$m=\frac{y_P-y_Q}{x_P-x_Q}$
2. 计算交点R的坐标$x_R=m^2-x_P-x_Q，y_R=y_P+m\left(x_R-x_P\right)or{y}_R=y_Q+m\left(x_R-x_Q\right)$
3. 得到坐标$\left(x_P,y_P\right)+\left(x_Q,y_Q\right)=\left(x_R,-y_R\right)$

有限域上的椭圆曲线

椭圆曲线是连续的，并不适合用于加密；所以，把椭圆曲线变成离散的点，即把椭圆曲线定义在有限域$GF(p)$上。形式如下，
{ ( x , y ) ∈ ( F p ) 2 ∣ y 2 ≡ x 3 + a x + b (   m o d   p ) , 4 a 3 + 27 b 2 ≢ 0 (   m o d   p ) } ∪ { 0 } \left\{(x, y) \in\left(\mathbb{F}_{p}\right)^{2} \mid y^{2} \equiv x^{3}+a x+b(\bmod p), 4 a^{3}+27 b^{2} \not \equiv 0(\bmod p)\right\} \cup\{0\} { (x,y)∈(Fp​)2∣y2≡x3+ax+b(modp),4a3+27b2≡0(modp)}∪{ 0}
连续的椭圆曲线在xy轴平面上表现为不相交的点集，如图，

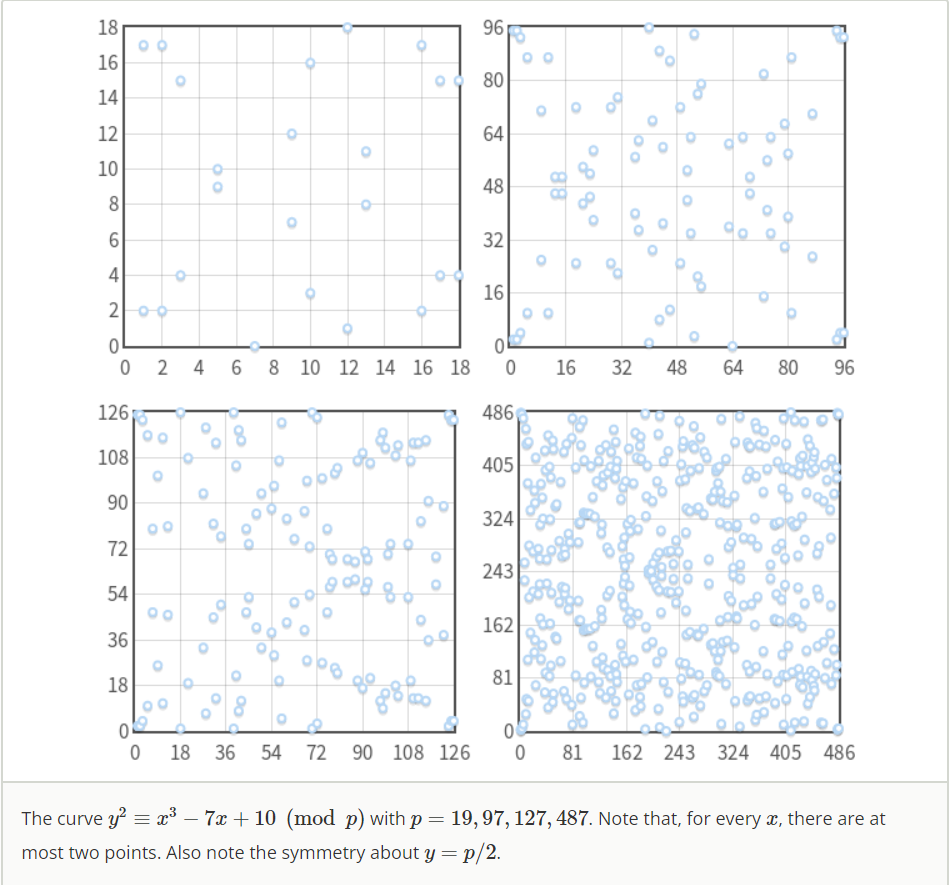
加法
域上的椭圆曲线加法还是定义为在同一直线的三点P，Q，R

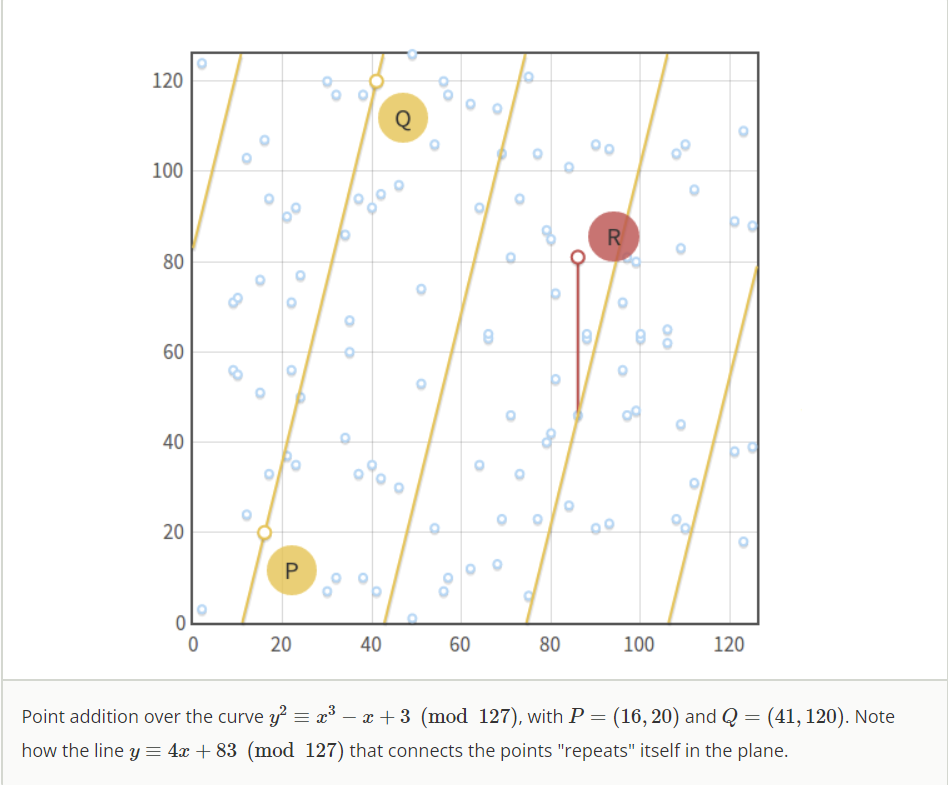
两点成一条线，有mod运算，所以线是不断重复的，其余计算在前文基础上加一个mod运算即可。

如果让$P=Q$那么将得到$P+P=2P=-R$ 进而得到一种数乘$nP=\underset{n\text{ times }}{\underbrace{P+P+\cdots +P}}$。
注意：这是点加，得到的结果是曲线上的点哦。

而定义在椭圆曲线上的这种数乘，将构成一个循环子群，也就是存在一个n，使得$nP=0$，这和模加的运算类似，也就是说，nP的集合是一个循环阿贝尔群。这里的P就是循环子群的生成元或者基点。
椭圆曲线的阶：群的阶表示为群中有多少个点，所以椭圆曲线的阶就是曲线上的点的数目N
**椭圆曲线上某一点的阶：**也就是基点P的阶，定义为满足$nP=0$的n。
由拉格朗日定理，子群的阶是父群的阶的因子。可以通过找N的所有因子，来找n。也就是说有$NP=n(hP)=0$,h永远为一个整数，令$G=hP$，可以得到点G生成了一个阶为n的一个子群。

一般离散对数问题

给定一个整数b和一个质数p的一个原根a，找到一个唯一的指数i，使得 $b=a^i\mathrm{mod}p$成立，其中$0\le i\le p-1$。

椭圆曲线上的离散对数问题

是指给定两个椭圆曲线上的点 G 和 H，找到一个整数 d，使得$H=dG$

算法思想

ElGamal
基于离散对数问题

EC EIGamal
简单描述，私钥为小于子群阶n的整数d，即 d ∈ { 1 , … , n − 1 } d \in \{1,\dots,n-1\} d∈{ 1,…,n−1}，公钥为点H，即$H=dG$，G为子群的基点，根据椭圆曲线上的离散对数难题得知，知道H和G求得d是很难的。

DSA

数字签名算法，安全性依赖于离散对数问题。
大致过程
主要参数

• p：大素数
• q：q是 p-1的一个素因子
• y：$y=g^x\mathrm{mod}p$
• g：$g=h^{(p-1)/q}\mathrm{mod}p$,(1<h<p-1)

以上为公开的参数

• x：随机私钥，0<x<p
• k：随机数，0<k<p
• H：哈希

签名：
$r=(g^k\mathrm{mod}p)\mathrm{mod}q$
$s=k^{-1}(H(m)+xr)）\mathrm{mod}q$
签名为(r,s)
验证：
分别计算$w=s^{-1}\mathrm{mod}q$,$u_1=（H(m)\times w）\mathrm{mod}q$,$u_2=(rw)\mathrm{mod}q$和$v=((g^{u_1}\times y^{u_2})\mathrm{mod}p)\mathrm{mod}q$
然后比较v和r，相等则验证成功。

ECDSA

ECC+DSA，广泛用于数字加密货币
签名过程和DSA类似，需要选用安全的哈希函数，为了使哈希结果的比特长度和子群的阶n的比特长度一致，消息的哈希结果需要被截断，被截断后的哈希值会是一个整数。后文暂定为z，即$z=H(m)$。
大致过程
$H_A=d_{A}G$公钥为$H_A$,私钥为$d_A$。

• 签名
  1. 选择一个随机数$k,(1<k<n)$n为子群的阶
  2. 计算$P=kG$,G为子群的基点
  3. 计算$r=x_p\mathrm{mod}n$，x为点P的x轴坐标，若$r=0$则重新选一个k来计算
  4. 计算$s=k^{-1}(z+r{d}_A)\mathrm{mod}n$，z为被截断的消息哈希值，是一个整数，$d_A$是私钥，如果$s=0$,重新选择一个k计算。
  5. $(r,s)$就作为签名。
• 验证
  1. 计算整数$u_1=s^{-1}z\mathrm{mod}n$
  2. 计算整数$u_2=s^{-1}r\mathrm{mod}n$
  3. 计算点$P=u_{1}G+u_2{H}_A$

正确性验证一下
KaTeX parse error: {align} can be used only in display mode.

涉及到阈值 ECDSA

Threshold cryptosystems

概述

基础概念

门限密码主要解决的是，传统公钥密码中由于私钥唯一，而可能导致的单点故障问题，如密钥丢失，单点权限过高或者该点被攻击者控制而导致安全风险问题等等。
它通过将密钥信息分享给多个用户分散保存, 密码功能操作可由至少门限值个用户 协作完成, 而且任意少于门限数量的用户无法进行合谋. 简而言之，就是密钥信息被拆成多个零散的碎片，由多个用户保存，其中一定数量的用户一起使用自己的密钥信息就可以合成密钥，这个数量就是门限。
这有点像特殊的多方安全计算， 多个用户秘密地分享了密钥 信息, 在进行解密/签名操作时, 用户可使用自己的私钥, 通过多方安全计算的模式多方协作解密密文/签名消息。
这样做，一方面提高了系统的健壮性, 即使少量用户丢失 密钥, 不会导致密码系统丧失功能性. 另一方面, 提高了系统的安全性, 恶意敌手即使窃取了部分 (少于门限值) 用户的密钥, 也难以打破密码系统的安全性。

分类

• 门限密码主要包括门限加密和门限签名，这和传统公钥中的两种操作类似。
• 全分布式和非交互式：系统公钥和各个用户私钥是由用户们自行交互生成，而不需要密钥生成中心，则称全分布式的门限密码。而在解密/签名时，无需用户之间或者和用户和组合器之间的交互的话，则称为非交互式的门限密码

攻击模型

• 静态攻击模型： 敌手在系统参数发布前先选定攻击的目标用户, 可获得目标用户的私钥信 息
• 自适应攻击模型： 敌手可在系统运行的任何时刻，根据具体的攻击情况自适应地选择攻击的目标用户, 获得目标用户的私钥信息

一些特性

• 紧致性：公钥尺寸和密文/签名尺寸与参与 用户的数量无关。
• 鲁棒性 ： 各用户的解密/签名分享的正确性可被公开验证。
• 全分布式：系统的公钥和用户的私钥可由用户自己通过交互生成, 避免了密钥生成中心的权限过大或者被攻击者 控制等带来的安全风险。
• 抗合谋：门限密码系统要求参与的用户数量达到门限值, 才能正确完成密码 操作, 防止了单个用户失败导致整个系统瘫痪, 同时防止任意少于门限值个用户合谋。

门限加密

它包含密钥生成、加解密、消息组合器（combiner）几个过程。 解密的时候用户使用自己的私钥解密 密文, 并将解密分享发送给消息组合器, 消息组合器在接收到门限值数量个解密分享时就可以组合还原出原消息。

算法

• $KeyGen(\lambda ,n,t):$ 密钥生成算法输入安全参数 λ, 用户数量 n 和门限值 t, 输出公钥 pk 和用户私钥分享$sk=(s{k}_{i{d}_1},\dots ,ski{d}_n)$
• $Enc(pk,m):$ 加密算法输入公钥 pk 和消息 m, 输出密文 c。
• $Dec(s{k}_{id},c):$ 解密算法输入任意用户的私钥分享 $s{k}_{id}$ 和密文 c, 输出解密分享 $c_{id}$。
• $Combine(c_{i{d}_{i1}},\dots ,c_{i{d}_{it}}):$ 消息组合算法输入任意 t 个解密分享 $c_{i{d}_{i1}},\dots ,c_{i{d}_{it}}$, 输出消息 m。

门限签名

它包括密钥生成、签名和验签过程, 以及一个签名组合器。签名时, 用户使用自己的私钥签名消息, 并将签名分享发送给签名组合器, 签名组合器在接收到门限值数量个签名分享时就可以组合还原出该消息的签名。

算法

• $KeyGen(\lambda ,n,t):$ 密钥生成算法输入安全参数 λ, 用户数量 n 和门限值 t, 输出验证公钥 vk 和用 户私钥 $sk=(s{k}_{i{d}_1},\dots ,s{k}_{i{d}_n})$。
• $Sign(s{k}_{id},m):$签名算法输入任意用户私钥 $s{k}_{id}$ 和消息 m, 输出签名分享 ${\sigma }_{id}$。
• $Combine({\sigma }_{i{d}_{i1}},\cdot \cdot \cdot ,{\sigma }_{i{d}_{it}}):$签名组合算法输入任意 t 个签名分享 ${\sigma }_{i{d}_{i1}},\cdot \cdot \cdot ,{\sigma }_{i{d}_{it}}$ , 输出签名 σ。
• $Verify(vk,m,\sigma ):$验证算法输入验证公钥 vk, 消息 m 和签名 σ, 当签名验证成功时输出 1, 否则输 出 0。

多重签名与门限签名
提一嘴多重签名，顾名思义，它依赖于拥有单独而且唯一的密钥的各方，需要他们用这些密钥来一个接着一个的对一笔交易签名，验证者就需要分别检查每一个签名。而门限签名只有一把公钥，一把密钥和一个签名，验证者只需验证一个签名即可。

Threshold ECDSA

基本概念

基于椭圆曲线数字签名算法（ECDSA）的分布式密钥生成和签名协议。它允许多个参与方共享一个ECDSA密钥对，并且只有当达到一定数量的参与方同意时才能生成有效的签名。
阈值ECDSA的工作原理大致如下：

1. 首先，参与方通过一个可信的设置协议生成一个共享的ECDSA密钥对，并将其分解为多个分片，每个参与方持有一个分片。
2. 然后，当需要签名一条消息时，参与方通过一个安全的多方计算协议计算出一个共享的随机数（nonce）和它对应的椭圆曲线点。
3. 接着，参与方使用自己的密钥分片和共享的nonce来计算出签名的一部分，并将其发送给其他参与方。
4. 最后，如果收到足够数量（达到阈值）的签名部分，任何一个参与方都可以将它们组合成一个完整的ECDSA签名，并将其附加到消息上。

G-DSA

这是个统一DSA和ECDSA两种方案的签名
公开的参数有

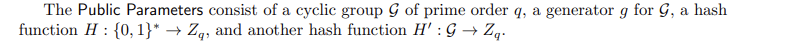
密钥生成，签名和验证


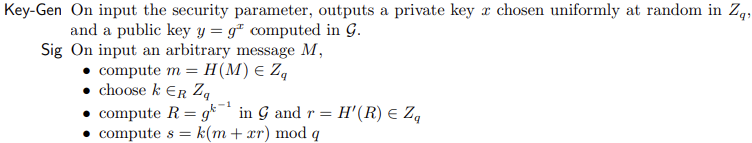
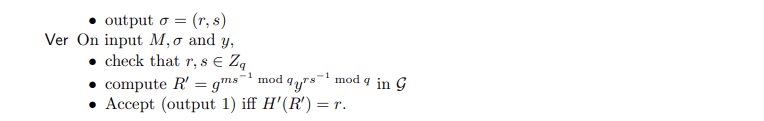
相关注释，不同方案的乘法操作和$H^{\prime }()$函数的处理不同。

DKG （Distributed Key Generation）

这里使用的是Pedersen’s DKG，然后增加了一些手段来保证安全。
下面是大致的描述
不需要Dealer的秘密共享$（n,t）$：

1. 首先每个参与者$P_i$随机选择一个秘密值$u_i$，计算一个陷门承诺$[KG{C}_i,KG{D}_i]=Commit(g^{u_i})$，并广播$KG{C}_i$承诺，同时每个参与者还需要广播自己的用于MtA的Paillier同态加密算法的公钥$E_i$。

下面是陷门承诺的方案描述。

2. 接着每个参与者公布$KG{D}_i$（用于承诺验证），让$y_i$作为解开的承诺，即$y_i=g^{u_i}$。公钥就是$Y={\prod }_{i=1}^n{y}_i$。

然后每个参与者都把自己的$u_i$作为主秘密，通过Feldman vss的方式分享给其他的参与者。
（也就是每个参与者都单独作为一个Dealer，每个人都随机选择一个$t-1$阶多项式，对所有人包括自己分发子秘密$f_{ui}(j)=u_{ij}$，每个人的标号不变，固定$[1,n]$，这样每个人加上自己的会收到共$n$个子秘密值）

3. 最后每个参与者都把自己收到的秘密值加起来（$n$个）得到$f_X(i)=x_i={\sum }_{j=1}^n{u}_{ij}$，这样整体的秘密值（私钥）$X={\sum }_{i=1}^n{x}_i$

Signature Generation

签名思路

要把ECDSA算法改为分布式的，核心在于如何对算法里的某些参数进行合理的确保安全性的拆分。这里的主要思路是拆分ECDSA算法中的随机数为$k=\sum k_i$与私钥$x=\sum w_i$之和，只有参与者知道自己的数据。
求签名中的r
根据签名的G-DSA算法，求$r$需要求得$R=g^{k^{-1}}$，方案的思路为，引入一个变量$\gamma$，也拆分为几个之和。如下
$\begin{array}{rl}R& =g^{k^{-1}}\\ & =g^{\gamma k^{-1}{\gamma }^{-1}}\\ & =g^{\left(\sum {\gamma }_i\right)k^{-1}{\gamma }^{-1}}\\ & ={\left(g^{\left(\sum {\gamma }_i\right)}\right)}^{(k\gamma {)}^{-1}}\\ & ={\left(\prod g^{{\gamma }_i}\right)}^{(k\gamma {)}^{-1}}\end{array}$
每个参与者单独计算$g^{{\gamma }_i}$和${\sigma }_i=k_i{\gamma }_i$并公开，这样不会泄漏每个$k_i$和${\gamma }_i$。
求签名中的s
类似的，也是拆分为${\sigma }_i=k_i{w}_i$的和的形式，如下（假设有三个参与者）
$\begin{array}{rl}s& =k(m+xr)\\ & =\left(\sum k_i\right)m+kxr\\ & =\left(k_1+k_2+k_3\right)m+\left({\sigma }_1+{\sigma }_2+{\sigma }_3\right)r\\ & =\left(m{k}_1+r{\sigma }_1\right)+\left(m{k}_2+r{\sigma }_2\right)+\left(m{k}_3+r{\sigma }_3\right)\\ & =s_1+s_2+s_3=\sum s_i\end{array}$

MtA（Multiplicative-to-Additive）

乘法转加法，需要用到加法同态算法（这里是paillier算法）。为什么用？因为乘法会使得多项式的阶数翻倍，从而让签名的门限人数增加，必须要让它降下来。
该协议功能为在双方不泄露自己的$a$和$b$的情况下，可以分别得到另外一个秘密值$\alpha$和$\beta$。
$ab=\alpha +\beta \mathrm{mod}q$
协议流程
假设有两个用户A和B

1. A to B：

发送$c_A=E_{p{k}_A}(a)$

2. B to A：

选择一个$\beta$，计算发送$b{\times }_{c_A}{+}_{c_A}{E}_A(-\beta )=E_{p{k}_A}(ab-\beta )$
注意符号，具体计算看看这个，

3. A解密即可得到$\alpha$

签名流程

一共五个阶段，首先根据MtA协议求得人数为$t$

1. Phase 1

• 每位参与者随机选取$k_i$和${\gamma }_i$（前面思路拆分中有提到），$k=\sum k_i,\gamma =\sum {\gamma }_i$
• 计算承诺

计算$Commit(g^{{\gamma }_i})=[C_i,D_i]$，并公布$C_i$

2. Phase 2

每两个人之间都进行两次MtA协议。

• 第一次MtA协议：（计算$k\gamma$）

$P_i,P_j$对$k_i,{\gamma }_j$使用MtA，将$P_i$得到的结果记为${\alpha }_{ij}$，将得到的结果记为${\beta }_{ij}$，得到$k_i{\gamma }_j={\alpha }_{ij}+{\beta }_{ij}$
定义${\delta }_i=k_i{\gamma }_i+{\sum }_{j\ne i}{\alpha }_{ij}+{\sum }_{j\ne i}{\beta }_{ji}$，这样如果每位参与者都公开自己的${\delta }_i$，所有参与者就可以在不公布自己的$(k_i,{\gamma }_i)$的情况下求得$k\gamma =(\sum k_i)\cdot (\sum {\gamma }_i)=\sum {\delta }_i$。
举例
假设有三个人，分别选择$(k_1,{\gamma }_1),(k_2,{\gamma }_2),(k_3,{\gamma }_3)$，这样两两进行两次MtA协议（一共六次），将得到$[k_1\gamma_2,k_1\gamma_3],[k_2\gamma_1,k_2\gamma_3],[k_3\gamma_1,k_3\gamma_2]$3对，6个值，再加上自己的三个值$k_1\gamma_1,k_2\gamma_2,k_3\gamma_3$就能组成$\delta_i$，如$\delta_1 = k_1\gamma_1+\alpha_{12}+\alpha_{13}+\beta_{21}+\beta_{31}$，一共3组。

• 第二次MtA协议：（计算$kx$）

类似第一次的，$P_i,P_j$对$k_i,w_j$使用MtA，将$P_i$得到的结果记为${\mu }_{ij}$，将得到的结果记为${\nu }_{ij}$，得到$k_i{w}_j={\mu }_{ij}+{\nu }_{ij}$，同样的定义${\sigma }_i=k_i{w}_i+{\sum }_{j\ne i}{\mu }_{ij}+{\sum }_{j\ne i}{\nu }_{ji}$，这样也可以和上面类似，求得$kx=(\sum k_i)\cdot (\sum w_i)=\sum {\sigma }_i$。

3. Phase 3

每位参与者都公开自己的${\delta }_i$，所有参与者计算出$k\gamma$

4. Phase 4 （求$r$）

• 所有参与者公布$D_i$，让${\Gamma }_i=g^{{\gamma }_i}$作为承诺解开的值，然后求得$R=[\prod {\Gamma }_i{]}^{{\delta }^{-1}}=g^{k^{-1}}$，最后求出$r=H^{\prime }(R)$

5. Phase 5（求$s$）

$s$是一个Additive Sharing。
每位参与者计算$s_i=m{k}_i+r{\sigma }_i$，求和$s=\sum s_i$就可以得到$s$。
这里没有选择直接公布${\sigma }_i$，而是增加了一系列验证手段来提升安全性。如下

• 这里引入了一组随机的$g^{{\ell }_i}$值用作$R^{s_i}$的掩码，形成加码后的$V_i=R^{s_i}{g}^{{\ell }_i}$

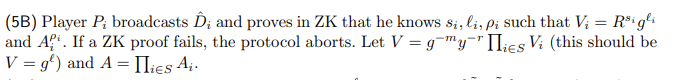
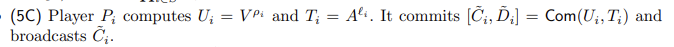
• 那么显然不能通过暴露$g^{{\ell }_i}$去检查$V$的正确性，于是又引入了一个$U

=g^{\ell_\rho}$

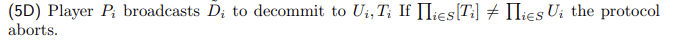
• 然后是各位参与者一起通过分布式DH交换来计算$U$，验证成功后还原$s$

Reshare

也就是动态的改变门限，假定为(5,3)，要变为(8,5)。

(n,t) to Additive Sharing方法

它，将Feldman-VSS方案转换为Additive sharing方案，假设整体的秘密（私钥）是$X$，用Feldman VSS方案得到一组门限$(n,t)$的子秘密$x_i$，现在要将这个方案变为转换为划分数为$X=\sum t_i$的加法分享方案。
原理就是拉格朗日插值法，详见秘密共享。
具体的方案就是$t_i={\lambda }_i\cdot x_i$得到，其中${\lambda }_i$是对应的拉格朗日系数，也就是$\ell (x)={\prod }_{j=0,i\ne j}^t\frac{x-x_j}{x_i-x_j}$。（系数特点是，在$x=x_i$的时候取值为1，在其他值取值为0）。

转换方法

具体方法是先使用调用(n,t) to Additive Sharing方法，将它转化为Additive Sharing，这里是将总体的秘密值转换为了3个之和，然后选择5位新增参与者选择随机数秘密值为$u_i=0$,代入DKG流程，这样就把总数变为了8，期间选择的多项式为4阶的即可将门限变更为5。这样就可以改变门限。

参考

椭圆曲线加密算法（中文翻译） 英文原文
椭圆密码学原理
ECC椭圆曲线详解
DSA简介
Multiparty Threshold ECDSA
Commitment Scheme
TU B B, CHEN Y. A Survey of Threshold Cryptosystems. Journal of Cryptologic Research. 2020, 7(1): 1-14 https://doi.org/10.13868/j.cnki.jcr.000344
Rosario Gennaro and Steven Goldfeder. 2018. Fast Multiparty Threshold ECDSA with Fast Trustless Setup. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security (CCS '18). Association for Computing Machinery, New York, NY, USA, 1179–1194. DOI:https://doi.org/10.1145/3243734.3243859