逻辑代数的基本公式
基本公式
逻辑代数的基本公式
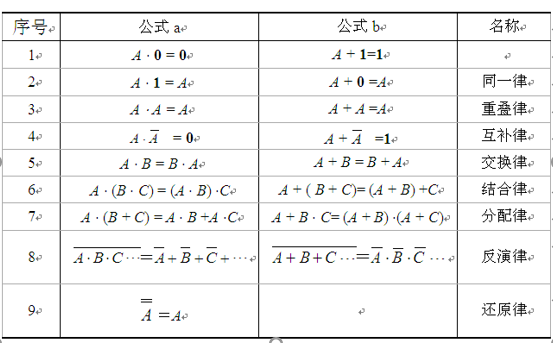
-
0、1律: A + 0 = A A + 1 = 1 A ⋅ 1 = A A ⋅ 0 = 0 A+0=A \quad A+1=1 \quad A \cdot 1=A \quad A \cdot 0=0 A+0=AA+1=1A⋅1=AA⋅0=0
-
互补律: A + A ˉ = 1 A ⋅ A ˉ = 0 A+\bar{A}=1 \quad A \cdot \bar{A}=0 A+Aˉ=1A⋅Aˉ=0
-
交换律: A + B = B + A A ⋅ B = B ⋅ A A+B=B+A \quad A \cdot B=B \cdot A A+B=B+AA⋅B=B⋅A
-
结合律: A + B + C = ( A + B ) + C A ⋅ B ⋅ C = ( A ⋅ B ) ⋅ C A+B+C=(A+B)+C \quad A \cdot B \cdot C=(A \cdot B) \cdot C A+B+C=(A+B)+CA⋅B⋅C=(A⋅B)⋅C
-
分配律: A ( B + C ) = A B + A C A + B C = ( A + B ) ( A + C ) A(B+C)=A B+A C \quad A+B C=(A+B)(A+C) A(B+C)=AB+ACA+BC=(A+B)(A+C)
-
重叠律: A + A = A A ⋅ A = A A+A=A \quad A \cdot A=A A+A=AA⋅A=A
-
反演律: A + B ‾ = A ˉ ⋅ B ˉ A B ‾ = A ˉ + B ˉ \quad \overline{A+B}=\bar{A} \cdot \bar{B} \quad \overline{A B}=\bar{A}+\bar{B} A+B=Aˉ⋅BˉAB=Aˉ+Bˉ
-
吸收律:
A + A ⋅ B = A A ⋅ ( A + B ) = A A + A ˉ ⋅ B = A + B ( A + B ) ⋅ ( A + C ) = A + B C \begin{array}{ll} A+A \cdot B=A & A \cdot(A+B)=A \\ A+\bar{A} \cdot B=A+B & (A+B) \cdot(A+C)=A+B C \end{array} A+A⋅B=AA+Aˉ⋅B=A+BA⋅(A+B)=A(A+B)⋅(A+C)=A+BC
-
其他常用恒等式:
A B + A ˉ C + B C = A B + A ˉ C A B + A ˉ C + B C D = A B + A ˉ C \begin{array}{l} A B+\bar{A} C+B C=A B+\bar{A} C \\ A B+\bar{A} C+B C D=A B+\bar{A} C \end{array} AB+AˉC+BC=AB+AˉCAB+AˉC+BCD=AB+AˉC
常用公式
A + B ‾ = A ‾ ⋅ B ‾ A B ‾ = A ‾ + B ‾ A + A ⋅ B = A A + A ˉ ⋅ B = A + B A ⋅ ( A + B ) = A A B + A B ‾ = A A ⊕ 0 = A A ⊙ 0 = A ‾ A ⊕ 1 = A ‾ A ⊙ 1 = A \begin{array}{ll} \overline{\boldsymbol{A}+\boldsymbol{B}}=\overline{\boldsymbol{A}} \cdot \overline{\boldsymbol{B}} & \overline{\boldsymbol{A B}}=\overline{\boldsymbol{A}}+\overline{\boldsymbol{B}} \\ A+A \cdot B=A & A+\bar{A} \cdot B=A+B \\ A \cdot(A+B)=A & \boldsymbol{A B}+\mathbf{A} \overline{\boldsymbol{B}}=\boldsymbol{A} \\ \boldsymbol{A} \oplus \mathbf{0}=\boldsymbol{A} & \boldsymbol{A} \odot \mathbf{0}=\overline{\boldsymbol{A}} \\ \boldsymbol{A} \oplus \mathbf{1}=\overline{\boldsymbol{A}} & \boldsymbol{A} \odot \mathbf{1}=\boldsymbol{A} \end{array} A+B=A⋅BA+A⋅B=AA⋅(A+B)=AA⊕0=AA⊕1=AAB=A+BA+Aˉ⋅B=A+BAB+AB=AA⊙0=AA⊙1=A

示例
1.证明 A + B ‾ = A ˉ ⋅ B ˉ \overline{A+B}=\bar{A} \cdot \bar{B} A+B=Aˉ⋅Bˉ,$ \quad \overline{A B}=\bar{A}+\bar{B}$
列出等式、右边的函数值的真值表
A B A ˉ B ˉ A + B ‾ A ˉ ⋅ B ˉ A B ‾ A ˉ + B ˉ 0 0 1 1 0 + 0 ‾ = 1 1 0 ⋅ 0 ‾ = 1 1 0 1 1 0 0 + 1 ‾ = 0 0 0 ⋅ 1 ‾ = 1 1 1 0 0 1 1 + 0 ‾ = 0 0 1 ⋅ 0 ‾ = 1 1 1 1 0 0 1 + 1 ‾ = 0 0 1 ⋅ 1 ‾ = 0 0 \begin{array}{|cc|cc|c|c|c|c|} \hline A & B & \bar{A} & \bar{B} & \overline{A+B} & \bar{A} \cdot \bar{B} & \overline{A B} & \bar{A}+\bar{B} \\ \hline 0 & 0 & 1 & 1 & \overline{0+0}=1 & 1 & \overline{0 \cdot 0}=1 & 1 \\ \hline 0 & 1 & 1 & 0 & \overline{0+1}=0 & 0 & \overline{0 \cdot 1}=1 & 1 \\ \hline 1 & 0 & 0 & 1 & \overline{1+0}=0 & 0 & \overline{1 \cdot 0}=1 & 1 \\ \hline 1 & 1 & 0 & 0 & \overline{1+1}=0 & 0 & \overline{1 \cdot 1}=0 & 0 \\ \hline \end{array} A0011B0101Aˉ1100Bˉ1010A+B0+0=10+1=01+0=01+1=0Aˉ⋅Bˉ1000AB0⋅0=10⋅1=11⋅0=11⋅1=0Aˉ+Bˉ1110
可见上面每个等式两边的真值表相同,故等式成立。
2.用基本公式证明下列等式成立。
A ˉ B + A B ˉ ‾ = A ˉ B ˉ + A B \overline{\bar{A} B+A \bar{B}}=\bar{A} \bar{B}+A B AˉB+ABˉ=AˉBˉ+AB
证明:
A ˉ B + A B ˉ ‾ = A ˉ ‾ B ⋅ A ˉ ‾ B ˉ ‾ = ( A + B ˉ ) ⋅ ( A ˉ + B ) = A A ˉ + A B + A ˉ B ˉ + B ˉ B = 0 + A B + A ˉ B ˉ + 0 = A ˉ B ˉ + A B \begin{aligned} \overline{\bar{A} B+A \bar{B}} & =\overline{\bar{A}} B \cdot \overline{\bar{A}} \overline{\bar{B}} \\ & =(A+\bar{B}) \cdot(\bar{A}+B) \\ & =A \bar{A}+A B+\bar{A} \bar{B}+\bar{B} B \\ & =0+A B+\bar{A} \bar{B}+0 \\ & =\bar{A} \bar{B}+A B \end{aligned} AˉB+ABˉ=AˉB⋅AˉBˉ=(A+Bˉ)⋅(Aˉ+B)=AAˉ+AB+AˉBˉ+BˉB=0+AB+AˉBˉ+0=AˉBˉ+AB
3.求证 A B + A ˉ C + B C = A B + A ˉ C A B+\bar{A} C+B C=A B+\bar{A} C AB+AˉC+BC=AB+AˉC
左式 = A B + A ˉ C + ( A + A ˉ ) B C = A B + A ˉ C + A B C + A ˉ B C = A B + A ˉ C \begin{aligned} \text { 左式 } & =A B+\bar{A} C+(A+\bar{A}) B C \\ & =A B+\bar{A} C+A B C+\bar{A} B C \\ & =A B+\bar{A} C \end{aligned} 左式 =AB+AˉC+(A+Aˉ)BC=AB+AˉC+ABC+AˉBC=AB+AˉC
4.求证 A B + A ˉ C + B C D = A B + A ˉ C A B+\bar{A} C+B C D=A B+\bar{A} C AB+AˉC+BCD=AB+AˉC
左式 = A B + A ˉ C + B C + B C D = A B + A ˉ C + B C = A B + A ˉ C \begin{array}{l} \text { 左式 }=A B+\bar{A} C+B C+B C D \\ =A B+\bar{A} C+B C \\ =A B+\bar{A} C \end{array} 左式 =AB+AˉC+BC+BCD=AB+AˉC+BC=AB+AˉC
逻辑代数的基本规则
代入规则
在包含变量A逻辑等式中,如果用另一个函数式代入式中所有A的位置,则等式仍然成立。这一规则称为代入规则。
A ⋅ B ‾ = A ˉ + B ˉ \overline{A \cdot B}=\bar{A}+\bar{B} A⋅B=Aˉ+Bˉ
用B·C 代替B,得 A ( B C ) ‾ = A ˉ + B C ‾ = A ˉ + B ˉ + C ˉ \overline{A(B C)}=\bar{A}+\overline{B C}=\bar{A}+\bar{B}+\bar{C} A(BC)=Aˉ+BC=Aˉ+Bˉ+Cˉ
得代入规则可以扩展所有基本公式或定律的应用范围
反演规则
对于任意一个逻辑表达式L,若将其中所有的与(• )换成或(+),或(+)换成与(•);原变量换为反变量,反变量换为原变量;将1换成0,0换成1;则得到的结果就是原函数的反函数。
1.试求 L = A ˉ B ˉ + C D + 0 L=\bar{A} \bar{B}+C D+0 L=AˉBˉ+CD+0的非函数。
解:按照反演规则,得
L ˉ = ( A + B ) ⋅ ( C ˉ + D ˉ ) ⋅ 1 = ( A + B ) ( C ˉ + D ˉ ) \bar{L}=(A+B) \cdot(\bar{C}+\bar{D}) \cdot 1=(A+B)(\bar{C}+\bar{D}) Lˉ=(A+B)⋅(Cˉ+Dˉ)⋅1=(A+B)(Cˉ+Dˉ)
2.试求 L = A + B C ˉ + D + E ˉ ‾ ‾ L=A+\overline{B \bar{C}+\overline{D+\bar{E}}} L=A+BCˉ+D+Eˉ的非函数 L ‾ \overline{L} L
解:由反演规则,可得 L ˉ = A ˉ ⋅ ( B ˉ + C ) ⋅ D ˉ E ‾ ‾ \bar{L}=\bar{A} \cdot \overline{(\bar{B}+C) \cdot \overline{\bar{D} E}} Lˉ=Aˉ⋅(Bˉ+C)⋅DˉE,保留反变量以外的非号不变。
对偶规则
对于任何逻辑函数式,若将其中的与(• )换成或(+),或(+)换成与(•);并将1换成0,0换成1;那么,所得的新的函数式就是L的对偶式,记作 L ′ L^{\prime} L′。
3.逻辑函数 L = ( A + B ˉ ) ( A + C ) L=(A+\bar{B})(A+C) L=(A+Bˉ)(A+C)的对偶式为
L ′ = A B ˉ + A C L^{\prime}=A \bar{B}+A C L′=ABˉ+AC
当某个逻辑恒等式成立时,则该恒等式两侧的对偶式也相等。这就是对偶规则。利用对偶规则,可从已知公式中得到更多的运算公式。
参考文献:
- Verilog HDL与FPGA数字系统设计,罗杰,机械工业出版社,2015年04月
- Verilog HDL与CPLD/FPGA项目开发教程(第2版), 聂章龙, 机械工业出版社, 2015年12月
- Verilog HDL数字设计与综合(第2版), Samir Palnitkar著,夏宇闻等译, 电子工业出版社, 2015年08月
- Verilog HDL入门(第3版), J. BHASKER 著 夏宇闻甘伟 译, 北京航空航天大学出版社, 2019年03月