基于阈值控制的一种改进鲸鱼算法-附代码

基于阈值控制的一种改进鲸鱼算法

摘要： 针对鲸鱼算法在迭代后期种群多样性减少问题,本文提出一种基于阈值控制的改进鲸鱼优化算法（简记为TIWOA）,将均匀分布空间与伪反向学习策略相结合,对原始种群位置进行初始化,为全局搜索奠定基础;改进了基于正态变异算子的选择种群方案,增加了局部搜索速度;设计了非线性收敛因子,配合改进的基于正弦函数的螺旋位置更新,使算法在迭代后期有更好的全局搜索能力。

1.鲸鱼优化算法

基础鲸鱼算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/107559167

2. 改进鲸鱼优化算法

2.1 基于均匀分布空间与伪反向学习策略的种群初始化

对于启发式智能优化算法来说, 初始迭代点的好坏往 往影响着收敛的速度与精度 $า$ ר 。原始 WOA算法在初始 化种群个体时使用了随机方法, 使用这种随机方法求解一 个多峰函数时, 若生成的初始种群相对集中在某个区域或 者分散在离最优点较远的峰, 则通过算法进行计算, 很可 能得到局部最优解。因此, 在初始点的选择上, 应尽可能 分布在不同维数的各个位置, 最大程度地提取求解函数中 的信息, 保障初始点的多样性。基于以上考虑, 结合对立 学习策略, 提出了一种均匀分布空间的种群个体随机方 法, 尽可能地将初始点均匀分布在可行域的空间里。具体 方法如下：
令求解函数可行域中, 每个维数的上确界集合为 ub $=\left[u{b}_1,u{b}_2,\cdots ,u{b}_d\right]$, 下确界集合为 $\mathrm{lb}=[{\mathrm{lb}}_1,{\mathrm{lb}}_2,\cdots$, $1{\mathrm{b}}_d]$, 则根据均匀分布空间初始化种群的方法, 第 $i$ 只鯨 鱼的第 $j$ 维的位置初始化公式如下所示：
$$X_i^{\prime }=\left({\mathrm{RNUM}}_i-1\right)\times \frac{\left({\mathrm{ub}}_j-1{\mathrm{b}}_j\right)}{N}+\mathrm{rand}\left(0,\frac{{\mathrm{ub}}_j-1{\mathrm{b}}_j}{N}\right)\text{\hspace{1em}(8)}$$
$$RNUM=randperm(NUM)\text{\hspace{1em}(9)}$$

其中, $\mathrm{rand}(a,b)$ 表示生成 $a$ 到 $b$ 之间的随机数, $\mathrm{NUM}=$ $\left[{\mathrm{NUM}}_1,{\mathrm{NUM}}_2,\cdots ,{\mathrm{NUM}}_N\right]$ 表示从 1 到种群个体总数 $N$ 的整数组成的数组, 其中 ${\mathrm{NUM}}_i=i$, randpcrm(NUM) 表 示将数组 NUM 中元萦的顺序随机打乱, 进行重新排列, 重新排列后的数组记为 $\mathrm{RNUM}=[{\mathrm{RNUM}}_1,\mathrm{RNUM}{\mathrm{N}}_2,\cdots$, ${\mathrm{RNUM}}_N]$, 数组 RNUM 依然是由 1 到 $N$ 的整数组成。 利用这样的方式, 能够将每个维数的可行域等分成 $N$ 个 小区间, 每只鲸鱼个体在随机不重复的在一个小区间上随 机取点, 这样使得初始点在每个维数上的取点更加均匀, 很大程度上减少算法得到局部最优解的概率。
对立学习策略 (opposition-based learning, OBL ) ${}^{-177}$ 是 近年来智能算法领域的一种新技术, 在 PSO 算法等智能 算法中成功应用后, 龙文等 已将该方法用于 $WO\wedge$ 算 法, 使得初始点的质量有了明显的提高, 但该方案在作用 域对称时, 对立学习的效果会有所淢弱。因此为了提高对 立学习的能力, 黄元春等在改进标准对立学习策略后, 提 出了伪反向学习策略的种群初始化方案 ${}^{-187}$, 具体步叕如 T:
在利用均匀分布空间的方法随机得到了第 $i$ 只鲸鱼 在可行域内的位置 $X_i=\left(X_i^1,X_i^2,\cdots ,X_i^d\right),i=1,2,\cdots$, $N$, 其中 $d$ 为维数, 则第 $i$ 只鲸鱼伪反向个体 ${\bar{X}}_i=({\bar{X}}_i^{\top }$, ${\bar{X}}_i^2,\cdots ,{\bar{X}}_i^d$ ) 的计算公式如下：
$${\tilde{X}}_i^j=ub+lb-X_i^j,j=1,2,\cdots ,d\text{\hspace{1em}(10)}$$

$$\begin{array}{c}{\bar{X}}_i^j=\{\begin{array}{l}\mathrm{rand}\left(M_j,{\tilde{X}}_i^j\right),X_i^j\le M_j\\ \mathrm{rand}\left({\tilde{X}}_i^j,M_j\right),X_i^j>M_j\end{array}\end{array}\text{\hspace{1em}(11)}$$
其中, $M_j=0.5(\mathrm{ub}-\mathrm{lb}),\mathrm{rand}\left({\tilde{X}}_i^j,M_j\right)$ 表示 $\left({\tilde{X}}_i^j,M_j\right)$ 内 的随机数。由均匀分布空间与伪反向学习策略初始化种群算法步聚如下:

2.2 基于正态变异的择优选择

正态变异算子 作为一种常见的智能算法干扰方 式, 在迭代前期会加快捜寻最优解的速度, 在迭代后期, 种 群的个体不断向最优个体集中, 导致种群多样性的减少, 利用正态变异算子可以丰富种群的多样性。通过该变异 方案与搜索包围机制, 螺旋更新位置结合, 可以在提高局 部搜索能力的同时,提高全局搜索范围,极大地提高搜寻 到最优解的概率和精度。
在之前的改进中, 钟明辉 等 将正态变异算子应用 于每次迭代后的最优个体, 本算法中的正态变异算子将推 广到对每个个体, 并且将变异后的个体与原个体的适应度 进行比较, 并且择优选择适应度小的个体代替当前个体进 人下一次迭代。再进过分析, 择优选择的方法会减弱全局 捜索能力, 故在全局搜寻阶段, 直接选择变异后的个体作 为当前个体, 不进行择优选择, 故第 $i$ 只鲸鱼的第 $j$ 维的 正态变异计算公式如下：
$${\bar{X}}_i^j=X_i^j+N(0,1)\cdot X_i^j\text{\hspace{1em}(12)}$$
选择变异前后的最优个体作为进人下一次迭代的个体, 其 计算公式如下:
$$X_{i+1}=\{\begin{array}{c}{f}^{-1}\left(\min \left(f\left(X_i\right),f\left({\bar{X}}_2\right)\right)\right),\\ f\left(X_i(t)\right)-f\left(X_i(t-s)\right)\ne 0\\ {\bar{X}}_i,f\left(X_i(t)\right)-f\left(X_i(t-s)\right)=0\end{array}\text{\hspace{1em}(13)}$$
其中, $N(0,1)$ 表示均值为 0 , 方差为 1 的标准正态分布,$f(X)$ 表示个体 $X$ 的适应度, $f^{-1}(\min (X,Y))$ 表示选择 适应度最小的 $X$ 或 $Y,s$ 表示阈值, 阈值的作用是为了检 验算法是否能够继续提高局部捜索的精度。 $X_i(t)$ 䘚示当 前个体第 $\mathrm{t}$ 次迭代后的位置, 若 $f\left(X_i(t)\right)-f\left(X_i(t-s)\right)$ $\ne 0$, 表示算法依然在有效的搜寻最优点以及提高局部搜 索的精度; 否则,说明算法在该局部的精度可能达到当前 算法方案的极限, 需要提高局部搜索和全局搜索能力。阈 值的取值林当重要, 若阈值太大, 则订算达到算法的极限 精度时,需要经过 $s$ 次迭代后, 才能检测到计算达到该精 度。

2.3 基于正弦函数的螺旋更新位置

在 $WO\wedge$ 算法中,螺旋更新位置是一种不断靠近当前 最优个体, 并且在最优个体附近进行捜索的方法。若陷人 局部最优解, 仅仅通过正态变异算子进行干扰很难跳出局 部最优解, 相对于 $\mathrm{W}\wedge \wedge$ 算法的收缩包围机制, 根据 $|A|$ 值可以向最优点进行局部搜索, 或者向随机点进行全局搜 索。根据上述思路, 吴泽忠等提出了一种基于正弦函数螺 旋更新位置的方案 ${}^{-137}$, 这种方法使得最优点可以向当前 迭代点进行包围搜索, 加强其全局搜索能力, 并且正弦函 数也能提高局部搜索的精度, 但是减弱了前期的收敛速 度。结合以上方案, 在保证收敛速度的前提下, 希望能在 局部搜索时对精度有更好的探索, 则改进的基于正弦函数 的螺旋更新位置计算公式为：
$$X_i^j(t)=\{\begin{array}{r}{\dot{D}}^{\prime }{e}^{bl}\cos (2\pi l)+X^{\ast }(t),\\ f\left(X^{\ast }(t)\right)-f\left(X^{\ast }(t-s)\right)\ne 0\\ {\dot{D}}^{\prime }{e}^{bl}\cos (2\pi l)+X_i^j(t)+\sin \left(X_i^j(t)\right)\\ f\left(X^{\ast }(t)\right)-f\left(X^{\ast }(t-s)\right)=0\end{array}\text{\hspace{1em}(14)}$$
其中, ${\dot{D}}^{\prime }=\left|X_i(t)-X^{\ast }(t)\right|$ 表示第 $i$ 条鲸鱼到当前最优 个体的直线距离。 $s$ 表示阈值, 其数值与公式(13)相同。 当算法依然在有效地提高局部搜索的精度时, 利用基本 woa算法的螺旋更新位置进行搜索; 当在该局部的精度 可能达到当前算法方案的极限时, 利用改进的基于正弦函 数的螺旋更新位置进行搜索。

2.4基于正弦函数的螺旋更新位置

本文提出的 $\mathrm{TIWO\Lambda }$ 算法, 通过正态变异算子, 基于 正弦函数的螺旋更新位置两种方案, 提高了后期的局部搜 索能力与全㟃搜索能力。通过实验发现由于前期迭代收 敛较快, 导致了随机搜索方法 (式 (7))更难得到适应度更 优的个体, 所以在前期迭代应使收敛因子 $a$ 大于 1 , 并且 快速减少到 1 以下, 故在 TIWOA算法中, 设计了一种收 敛因子 $a$ 非线性从 2 减少到 $0.5,a$ 减小的速度先快后 慢, 这样的设计使得前期能进行全局搜索的同时, 加快局 部捜索的速度,得到改进的非线性收敛因子公式为：
$$a=\{\begin{array}{ll}{\left(\frac{t-1}{T-1}\right)}^2+1,& 1\le t\le T\\ \frac{1}{2}{\left(\frac{t-T-1}{t_{\max }-T-1}\right)}^2+0.5,& T<t\le t_{\max }\end{array}\text{\hspace{1em}(15)}$$

$$T=floor\left(t_{\max }/50\right)\text{\hspace{1em}(16)}$$
其中, floor $(x)$ 表示对 $x$ 向下取整, 即不大于 $x$ 的整数。 这里的 $T$ 值为收敛因子 $a$ 的分界线,当迭代次数小于 $T$ 时, 收敛因子 $a>1$; 当迭代次数大于 $T$ 时, 收敛因子 $a<$ 1.

2.5 引入阈值判断函数是否达到局部最优解

TIWOA 算法利用阈值 $p$ 来判断算法是否达到了局部最优 解, 判断的方式如下:
$$P=\{\begin{array}{ll}1,& f\left(X^{\ast }(t)\right)-f\left(X^{\ast }(t-p)\right)\ne 0\\ 0,& f\left(X^{\ast }(t)\right)-f\left(X^{\ast }(t-p)\right)=0\end{array}\text{\hspace{1em}(17)}$$
其中, $P=1$ 时,算法根据式 (13)、式 (11)的判断条件来执 行对应的等式, 若 $P=0$ 时, 式 (13)、式 (11) 的判断条件强 制失效, 并强行执行情况(2)的方案。这样的改进能够更 好地调整算法方案, 增加迭代速度与求解精度。

3.实验结果

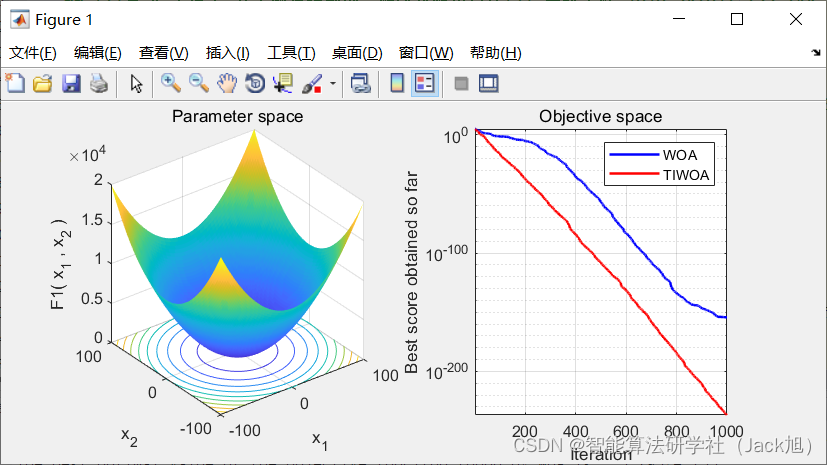
4.参考文献

[1]黄飞,吴泽忠.基于阈值控制的一种改进鲸鱼算法[J].系统工程,2020,38(02):133-148.

5.Matlab代码

6.Python代码