先介绍一下基本概念
以下基本概念转自其他的博客,不是原创
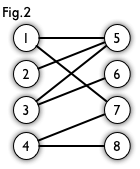
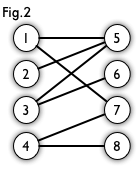
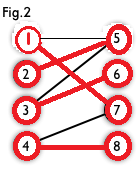
二分图:简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。准确地说:把一个图的顶点划分为两个不相交集 和 ,使得每一条边都分别连接 、 中的顶点。如果存在这样的划分,则此图为一个二分图。二分图的一个等价定义是:不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰,我们以后都把它画成图 2 的形式。
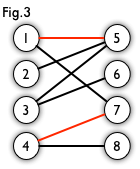
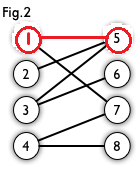
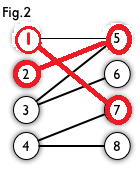
匹配:在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图 3、图 4 中红色的边就是图 2 的匹配
我们定义匹配点、匹配边、未匹配点、非匹配边,它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点,其他顶点为未匹配点;1-5、4-7为匹配边,其他边为非匹配边。
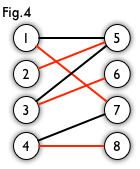
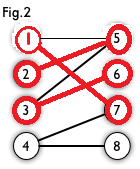
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 4 是一个最大匹配,它包含 4 条匹配边。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
上述是基本概念,接下来讲一下为匈牙利算法服务的一些概念
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边...形成的路径叫交替路。
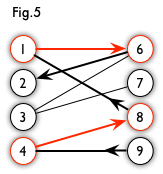
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。例如,图 5 中的一条增广路如图 6 所示(图中的匹配点均用红色标出):

增广路有一个重要特点:非匹配边比匹配边多一条。因此,研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边,所以这样做不会破坏匹配的性质。交换后,图中的匹配边数目比原来多了 1 条。其实,如果交替路以非匹配点结束的,那么这条交替路就是一条增广路
我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时,达到最大匹配(这是增广路定理)。匈牙利算法正是这么做的
接下来开始讲匈牙利算法
算法的基本思想:
基本思想:通过寻找增广路,把增广路中的匹配边和非匹配边的身份交换,这样就会多出一条匹配边,直到找不到增广路为止。
代码如下:
#include<bits/stdc++.h>
#define MAXN 9999
using namespace std;
int nx,ny;//nx表示二分图左边顶点的个数,ny表示二分图右边顶点的个数
int m;//m代表边的条数
int cx[MAXN],cy[MAXN];//如果有cx[i]=j,则必有cy[j]=i,说明i点和j点能够匹配
int x,y;//x点到y点有边
int e[MAXN][MAXN];//邻接矩阵
int visited[MAXN];//标记数组,标记的永远是二分图右边的顶点
int ret;//最后结果
int point(int u)//这个函数的作用是寻找增广路和更新cx,xy数组,如果找到了增广路,函数返回1,找不到,函数返回0。
{
for(int v=1;v<=ny;v++)//依次遍历右边的所有顶点
{
if(e[u][v]&&!visited[v])//条件一:左边的u顶点和右边的v顶点有连通边,条件二:右边的v顶点在没有被访问过,这两个条件必须同时满足
{
visited[v]=1;//将v顶点标记为访问过的
if(cy[v]==-1||point(cy[v]))//条件一:右边的v顶点没有左边对应的匹配的点,条件二:以v顶点在左边的匹配点为起点能够找到一条增广路(如果能够到达条件二,说明v顶点在左边一定有对应的匹配点)。
{
cx[u]=v;//更新cx,cy数组
cy[v]=u;
return 1;
}
}
}
return 0;//如果程序到达了这里,说明对右边所有的顶点都访问完了,没有满足条件的。
}
int main()
{
while (cin>>m>>nx>>ny)
{
memset(cx,-1,sizeof(cx));//初始化cx,cy数组的值为-1
memset(cy,-1,sizeof(cy));
memset(e,0,sizeof(e));//初始化邻接矩阵
ret=0;
while (m--)//输入边的信息和更新邻接矩阵
{
cin>>x>>y;
e[x][y]=1;
}
for(int i=1;i<=nx;i++)//对二分图左边的所有顶点进行遍历
{
if(cx[i]==-1)//如果左边的i顶点还没有匹配的点,就对i顶点进行匹配
{
memset(visited,0,sizeof(visited));//每次进行point时,都要对visited数组进行初始化
ret+=point(i);//point函数传入的参数永远是二分图左边的点
}
}
cout<<ret<<endl;
}
}
分析一下poiint函数是如何运行的,通过上图分析,第一次以1顶点为起点进入point(1)函数,然后5号顶点满足条件,更新cx[1],cy[5],返回1。此时1-->5这条边为匹配边,1号,5号顶点为匹配顶点
然后以2顶点为其实点进入point(1)函数,然后访问到5号节点,然后以5号节点的匹配点1号节点为起始点再次进入point(2)函数,找到了7号点,这时说明找到了增广路,然后更新cx[1],cy[7],然后返回1,更新cx[2],cy[5],返回一,函数结束。
然后以3号顶点为起始点进入point(1)函数,然后访问到5号节点,然后以5号节点的匹配点2号节点为起始点再次进入point(2)函数,找不到点了,返回0,到达point(1)函数,继续访问其他的节点。然后访问到6号顶点,满足条件,更新cx[3],cy[6],返回一,函数结束。
然后以4号顶点为起始点进入point(1)函数,然后访问到7号节点,然后以7号节点的匹配点1号节点为起始点再次进入point(2)函数,然后找到5号节点,然后以5号节点的匹配点2号节点为起始点再次进入point(3)函数,找不到点了,返回0,到达point(2)函数,继续访问其他的节点,没有点了,返回0,到达point(1)函数,继续访问其他的节点,到达了8号节点,满足,然后更新cx[4],cy[8],返回一,函数结束。
上图就是找到的所有的匹配边。