题目
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例
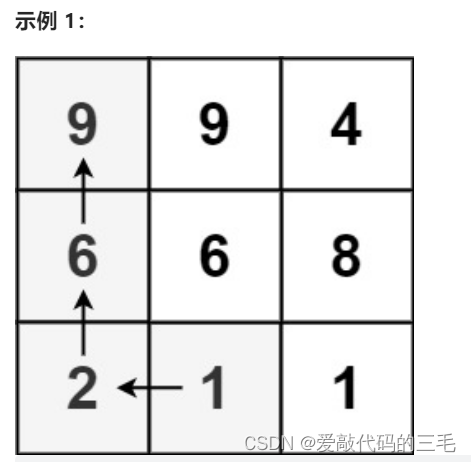
输入:matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
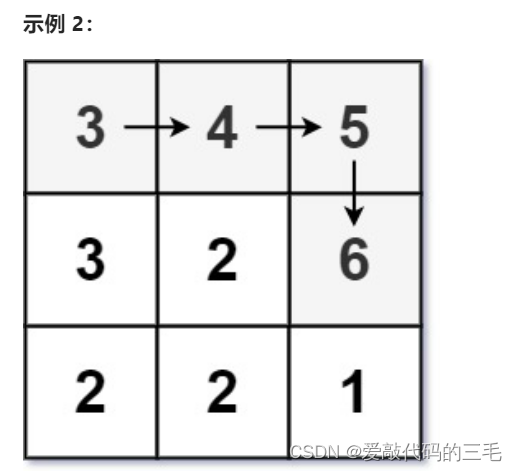
输入:matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
思路一(未通过)
直接dfs搜索
class Solution {
int[][] dpDownLeftRight = {
{
-1,0},{
1,0},{
0,1},{
0,-1}};
boolean[][] flag;
int row;
int col;
int count = 1;
int result = 1;
public void dfs(int[][] matrix, int x, int y) {
for (int i = 0; i < 4; i++) {
int newX = x + dpDownLeftRight[i][0];
int newY = y + dpDownLeftRight[i][1];
if (newX < 0 || newX >= row || newY < 0 || newY >= col || flag[newX][newY]) {
continue;
}
if (matrix[newX][newY] > matrix[x][y]) {
count++;
result = Math.max(count, result);
flag[newX][newY] = true;
dfs(matrix,newX,newY);
count--;
flag[newX][newY] = false;
}
}
}
public int longestIncreasingPath(int[][] matrix) {
row = matrix.length;
col = matrix[0].length;
flag = new boolean[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
flag[i][j] = true;
dfs(matrix,i,j);
flag[i][j] = false;
}
}
return result;
}
}
思路二
记忆化 dfs
定义一个和矩阵大小相同的数组,记录以及搜索的最大路径数,避免重复搜索
如果大于当前的路径数就更新,注意要加上当前自己的路径数1
class Solution {
int[][] upDownLeftRight = {
{
-1,0},{
1,0},{
0,-1},{
0,1}};
// 用来记录当前路径的最大值
int[][] mark;
int row;
int col;
public int dfs(int[][] matrix, int x, int y) {
if (mark[x][y] != 0) {
// 说明已经搜索过
return mark[x][y];
}
int max = 0;
for (int i = 0; i < 4; i++) {
int newX = upDownLeftRight[i][0] + x;
int newY = upDownLeftRight[i][1] + y;
if (newX < 0 || newX >= row || newY < 0 || newY >= col) {
continue;
}
// 只有当搜索的位置大大于当前位置才能继续走
if (matrix[newX][newY] > matrix[x][y]) {
// 在相邻四个点找最值
max = Math.max(max,dfs(matrix,newX,newY));
}
}
// 更新最大路径数,需要加上本身路径
mark[x][y] = max+1;
return mark[x][y];
}
public int longestIncreasingPath(int[][] matrix) {
row = matrix.length;
col = matrix[0].length;
mark = new int[row][col];
int result = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
result = Math.max(result,dfs(matrix,i,j));
}
}
return result;
}
}