背包问题是几个经典的问题之一,经典的问题去理解一下,理解好之后会形成一个印象,但是还需要做一些题目加以练习。
一、问题描述
一个旅行者随身携带一个背包。可以放入背包的物品有n 种, 每种物品的重量和价值分别为 wi, vi。 如果背包的最大重量限制是 b, 每种物品可以放多个。怎样选择放入背包的物品以使得背包的价值最大 ? 不妨设上述wi, vi, b 都是正整数
notes:背包有一个重量的约束,不能无限制的装入物品,被装的物品是不可以切割的,整体的装或者不装。另外如果物品数量没有限制的话,那其实就是一个完全背包问题,如果数量有限制,只能装进去1次或者不装进去那这就是0-1背包问题,现在我们研究完全背包问题。
二、实例分析
实例: n = 4,b =10
v1= 1, v2= 3, v3= 5, v4= 9,
w1= 2, w2= 3, w3= 4, w4= 7,
notes:现在我们看这个实例,有一个物品重量是:2,价值是:1(省去单位),第二个物品重量是:3,价值是:3(省去单位)。总限制b是:10。所以现在就是装第三个物品W3,就可以装第一个和第二个物品(4+3+2<10),而不能装第四个物品(4+7>10)。现在就需要想办法怎么去选择这些物品装到背包里面能达到最大。
1、建模
目标函数就在这里,其实是要求一个向量,这个向量就是物品装入背包,某一个物品的个数是xi ,将xi 乘上各自物品的价值,然后累计起来然后达到最大,这个就是我们要做的事情,约束条件就是背包重量的约束,每一个物品的重量乘上这个物品本身的数量然后累计起来(总重量)要小于等于b。
解是<x1, x2,…, xn>,其中xi 是装入背包的第 i 种物品个数
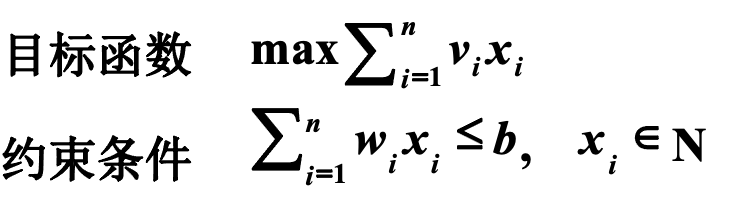
线性规划问题: 由线性条件约束的线性函数取最大或最小的问题
整数规划问题: 线性规划问题的变量 Xi都是非负整数
2、子问题界定和计算顺序
在背包问题里面依然是考虑物品的数量,物品的类别,如果在很多物品里面来考虑,可能这个问题比较困难,那可以将物品的个数缩小一点,比如一个子集里面来考虑,然后背包的重量的约束如果很小的话,其实很容易选择,背包重量大一点就不太好选择。
这个地方我们就可以考虑将物品的种类约束一下,将背包的重量也做一个约束,由这两个参数就可以确定一个子问题,现在另外一个问题就是,最优子结构是不是满足,当然最优子结构说的是背包。
原始背包问题里面b的值达到最大的时候,以及k所有物品都作为考虑对象的时候,要取的一个最优解,这个最优解,它是不是包含了它子问题的最优解。
(1)子问题界定:由参数k和y界定
k:考虑对物品1,2,…,k的选择
y:背包总重量不超过y
原始输入:k=n,y=b
(2)子问题计算顺序:
k=1,2……,n
对于给定的k,y=1,2,……,b
3、优化函数的递推方程
(1)原问题和子问题的递推关系是怎么样的?
和投资问题比较相似,取一个优化函数
前k种的意思是:将所有的物品做一个排列,这个排列其实是没有标准的,就是前k种,我们根据物品给定的序列给一个排列就好了,给我们的顺序是多少就把这个东西作为是一种物品的序列,然后在前k种物品里面考虑。

图上表示的就是前k种物品,在这个集合里面背包的重量不超过y,要把这些物品装入到背包里面,有一个最优的放置的方法,这个时候达到最优的时候总会有一个最好的方法,得到的价值达到最大时就把值称之为最大价值Fk(y)。
(2)接下来把问题规模扩大一点观察它们之间的关系
Fk(y) = max{ Fk-1(y) } , Fk( y-wk ) + Vk }

max:表示求最大
Fk-1(y):第k个物品不考虑了,就在前面的k-1个物品里来考虑,在约束是y的时候达到的一个最大的价值
Fk( y - wk ) + Vk :第k个物品要考虑先把它装一份进去,剩下的约束还是在前k个物品里来考虑,装进去之后加上Vk就是说装进去之后价值自然增加了一个Vk,在Fk里继续考虑,物品还可以继续的装进去,所以需要在前k个物品最优的装法里面继续来考虑,前面这项表示的是不考虑第k个物品,第k个物品完全不装,和至少装一份这是两种完全不同的选择,这两种选择到底哪一个好,如果哪一个更大它就更好。
(3)那么这两种哪一个更大呢?所以就取一个max符号,这个时候哪一个值更大,就构成在前k个物品考虑的时候,它的最好的装法其实是和前k-1个物品考虑的子问题之间非常强烈的关系,

这个关系就是第k个物品是完全不装到背包里面,另一种选择是至少要装一份第k个物品装进去。
剩下的背包依然在前k个物品里面去考虑,这个时候就有可能在装一份,这个时候就是完全背包。
如果是0-1背包的话,这个地方就是装一份和不装,这两种情况的选择,就不再是至少装一份和不把第k个物品完全装进去的这种选择。
(4)这个递推公式它所描绘的是子问题和原问题的这种递推
一开始的时候假定在k-1这个物品里面其实已经找到了最优解,已经得到一个最大值了,接下来就是在物品在扩展一点点的时候,能不能找到一个最大值,能不能找到它的最大值和它有没有什么关系,当然这个地方有一些初始的值,比如说现在没有任何物品背包重量是多大最大值都是0,背包总的重量是b,y是在[0,b]的区间里面。
背包的重量最大的约束就是0,背包其实不能装任何东西,Fk(0)=0,这个k的选择是[0,n],也就是说一开始没有任何的物品需要考虑就是0,物品的个数是从前1种,前2种,前3种……前k种这样依次去考虑。
F1(y)是比较好计算的,这个符号的含义表示前1种物品里面去装物品,约束是y,只要第一个物品有一点价值,就考虑把它装进去,其实它就是能装到最大,表示能装入第一个物品的最大的数量,然后把数量除以W1向下取整乘第一个物品的价值,就得到最大的值。
当y为负数的时候没有任何约束,这个背包其实已经超重了,超重是不允许的,所以这个时候最大的价值就是-∞。
(5)类似投资问题写的递推方程
这个地方xk做一个遍历,第k个物品到底是装0份,装1份,装2份,……,每一种情况都考虑一下。
不装就是装0份,装0份后考虑剩下的重量就完全拿给前k-1种物品来考虑, Fk-1( y - 0 )+0 ,装1份: Fk-1( y - 1 · vk)+ 1· vk,xk继续增长这种方程更好理解,但是不过没有上面的写法效率高。
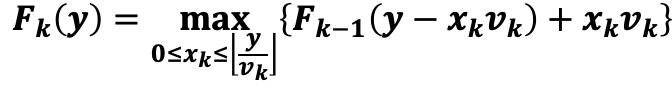
4、标记函数
ik(y): 装前 k 种物品, 总重不超 y, 背包达 到最大价值时装入物品的最大标号
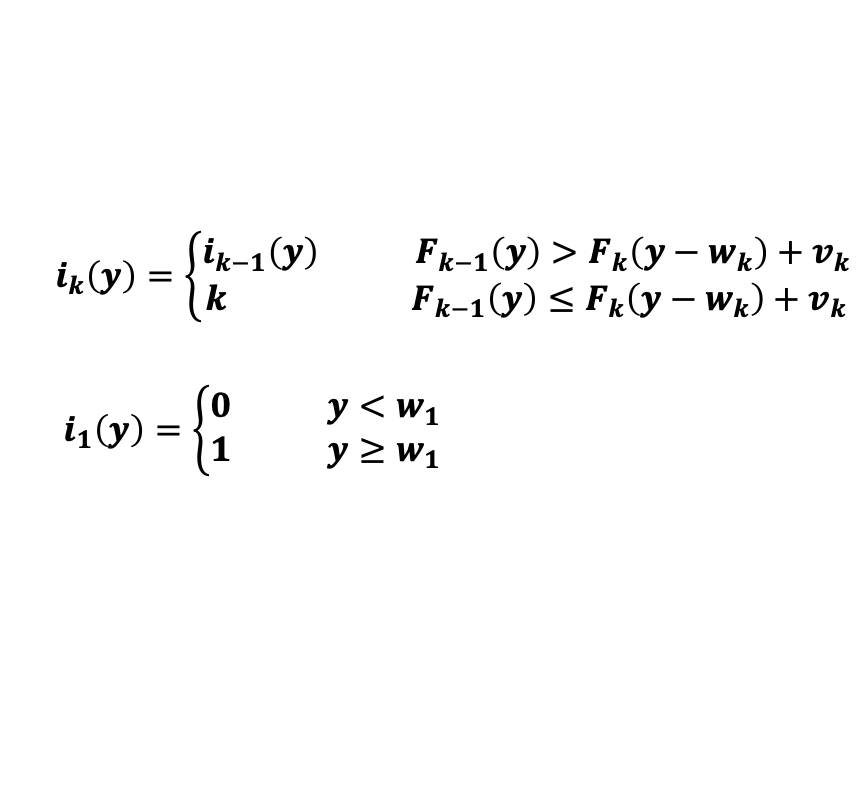
子问题重叠,在反复调用递推函数的时候,重复的调用了问题规模较小的子问题,所以在做背包问题的时候要设计备忘录,备忘录就是将子问题的解给存储起来的表格,存储背包问题,需要存 Fk,当约定k的时候k做横轴,y做纵轴,
三、实例
一共有4个物品,第一个物品重量是2,价值是1;第二个物品重量是3,价值是3;第三个物品重量是4,价值是5;第四个物品重量是7,价值是9。总的背包的约束重量是10(有10的最大的重量)
1、输入
v1 =1, v2=3, v3=5, v4=9,
w1=2, w2=3, w3=4, w4=7,
b=10
2、Fk (y) 的计算表
| k/y | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 2 | 0 | 1 | 3 | 3 | 4 | 6 | 6 | 7 | 9 | 9 |
| 3 | 0 | 1 | 3 | 5 | 5 | 6 | 8 | 10 | 10 | 11 |
| 4 | 0 | 1 | 3 | 5 | 5 | 6 | 9 | 10 | 10 | 12 |
每一行的坐标代表,y的值,也就是重量的约束,每一列是代表物品,只在第一个物品里面考虑——k取1;只在第一和第二个物品里面考虑——k取2……
首先我们来看第一行,y的取值,第一个物品能装多少个的问题。
① 第一行 k=1:
y=1时,所有物品的重量都大于1,所以最大价值为0
y=2时,能且只能装第一个物品,w1=y=2,最大价值为1
y=3时,可以装1个第一个物品,w1=2<y=3,最大价值为1
y=4时,4/2=2,可以装2个第一个物品,最大价值为2v1=2
y=5时,5/2=2.5向下取整为2,物品是不能切割的但是又不能超过重量,只能装2个第一个物品,价值单位为1,最大价值为2v1=2
y=6时,6/2=3,可以装3个第一个物品,最大价值为3v1=3
y=7时,7/2=3.5向下取整为3,物品是不能切割的但是又不能超过重量,只能装3个第一个物品,价值单位为1,1x3=3,价值取3,最大价值为3v1=3
y=8时,8/2=4,可以装4个第一个物品,最大价值为4v1=4
y=9时,9/2=4.5向下取整为4,物品是不能切割的但是又不能超过重量,只能装4个第一个物品,价值单位为1,1x4=4,价值取4,最大价值为4v1=4
y=10时,10/2=5,可以装5个第一个物品,最大价值为5v1=5
自底向上,其实这个问题是在逐渐扩大规模的,把y的值来扩展
② 第二行 k=2:
y=1时,所有物品的重量都大于1,所以为0
y=2时,在前两个物品里面考虑,第二个物品w2=3>y=2,所以第二个物品没有办法装进去,所以只能根据递推公式取第一个值(F1(2),0),这两者之中取最大,查表得F1(2)=1,最大价值为1
y=3时,在前两个物品里面考虑,F2(3)=max{F1(3),F2(3-w2)+V2}=max{1,3}=3,最大价值是3
……
只有查表,没有重复计算,这个是备忘录的优点
3、追踪解
(1)这个表会计算之后,再算12的时候其实是做了一个选择的,这个选择就是第4个物品确实要装1份,在求F4(10)的时候,其实是经过计算之后第4个物品,F4(10)在最后那个物品装进去之后就一定是第4,这个时候记录一下装入的最大物品的序号就是4,这个地方有1个4需要记录下来,表明当前这个选择装入的物品最大标号是4。
(2)ik(y)的值是需要被记录下来的,表示我们要追踪的时候,现在在前4个物品里面,如果重量约束是10的话,装入物品的最大的标号是4,表明4个物品至少要装1份,所以第4个物品是≥1的。
追踪解
| k/y | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 0 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 3 | 0 | 1 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 4 | 0 | 1 | 2 | 3 | 3 | 3 | 4 | 3 | 4 | 4 |
(3)接下来在追踪i2(3)的值,因为这个重量已经从10变成了3,减掉了7个,所以要查i4(3),这一项一查发现是2,2的含义是求得它的最大的时候,其实它装入物品最大的标号是2,所以第二个物品至少要装1份
(4)接着继续查询至i2(0),最大的标号是0,最后的解是第4个物品就等于1,第2个物品等于1,所以只装入这两个物品价值达到最大
i4(10)=4 → x4≥1
i4(10-w4)=i4(3)=2 → x2≥1, x4 =1, x3=0
i2(3-w2)=i2(0)=0 → x2=1, x1=0
解 x1=0, x2=1, x3=0, x4=1,价值12
四、追踪算法
输入: ik (y)表, k=1,2,…,n, y=1,2,…,b
输出: x1, x2,…,xn,n种物品的装入量
1. for k←1 to n do xk← 0
2. y←b, k←n
3. j←ik (y)
4. xk ←1
5. y←y- wk
6. while ik(y)=k do
7. y←y-wk
8. xk←xk+ 1
9. if ik(y)≠0 then goto 4
五、总结
动态规划算法解背包问题的算法里面,其实就是递归算法的用备忘录做了一个优化,可以这样去理解,一开始就不要去想表格该怎么样去设计,如果这样想就相当于把这个问题跨越了好几步,马上就变的很困难。
首先应该想到的原问题和子问题,子问题该怎么界定,然后再想原问题和子问题之间有没有最优子结构的关系,接着基于最优子结构的关系的基础上找出一个递推公式来,接下来就可以写递归算法,在得到递推方程之后,已经可以用递归的算法求解了。
在递归的基础上,设计一个表格来存储里面的东西,把子问题存储下来,其实就不用重复计算了。