动态规划是一类的方法的称呼,是一种思想,在很多问题上会用到这类方法。其中典型的动态规划应用的特点就是可以变成一个多阶段决策的过程。
比如在寻找路径的时候从最左边走到最右边其实是一个多阶段的过程,以及矩阵链的过程,也可以看作是矩阵链的子问题链条更小一点的问题,然后构成链条更大一点的子问题一直到原问题。这个时候更像是一个阶段的决策,更像是阶段性决策,可以转化成阶段性决策,另外一个重要的特点最优子结构,这句话说起来在《算法导论》里面也很多地方也写了这句话,最优解就是包含了子问题的最优解,也就是说什么是原问题什么是子问题,这个地方实际上是针对不同的问题是有不同的分割条件的。
矩阵链里面的子问题就是将原问题划分成两段的时候,不管怎样分割,最后一次分割的位置一旦确定以后,原问题就变成了两段,一个是在最后一次分割最后一次加括号的位置一定会分成左边和右边,左边这一段就是新的矩阵链相乘的问题,在这个里面依然存在要去找一个最好的括号化的方法,也就是往里面加括号,加入的括号能够得到最少的乘法的次数,然后原问题整个矩阵链从左边界到右边界分割成两段以后,原问题加括号的方法,在子问题里面加括号的方法加进去之后的乘法的次数,其实是一样的,原问题的最优的加括号的方法一定也是也是子问题的最优的加括号的方法,否则我们就可以用剪切粘贴的方法来构成一个新的最优解,最优子结构就不满足了。
一、剪切粘贴法
最优子结构:如果已经找到原问题最优的加括号的方法,那么这个加括号的方法去掉最后一层(最后一次加括号的位置),剩下的括号就分成左边和右边两部分。左边这部分相对于左边的矩阵链它依然是它的最优的解法(最优的加括号的方法),否则我们可以证明如果能找到一个更优的,那一开始找到原问题的那个就不是最优解,这个就叫做最优子结构的证明。
二、优化函数的递推方程
1、递推方程:
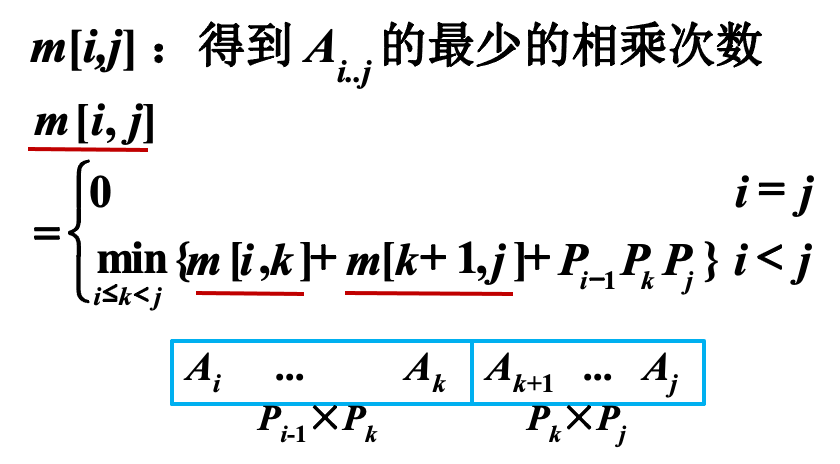
该问题满足优化原则
动态规划问题如果一开始找到了递推方程,或者可以写出原问题和子问题之间的关系,就马上可以用递归的算法来实现,在递归的过程中发现新的特点,有大量的子问题会重复的使用,子问题的解会重复的求解。在矩阵链的时候,会反复的求解链条长度更短的子问题,子问题的平均重复次数有多少个呢?就是把左右边界约定之后就是子问题,所有的子问题所有的次数加起来,只需要求一次就可以了,而不需要重复的求取,这样就可以继续改进递归的算法,将递归的算法在求解子问题的时候做一个备忘录,基于这个备忘录,可以大大的降低递归算法的时间复杂度,为了记录子问题,就要设计备忘录,备忘录一开始并没有存在,只是为了在递归的时候,为了提高递归的效率,做一个备忘录。基于备忘录就可以设计迭代的算法。
备忘录记录的东西根据具体问题具体分析,比如在矩阵链里面实际上记录的是给定遍边界的子问题,它的最少的计算次数,以及给定子问题之后最后一次加括号的位置,要记录下来,为了构造备忘录计算顺序是从低向上的先计算最小的子问题,然后在逐步的计算较大的子问题。
2、实例
很多时候当你确定这个问题具有最优子结构之后,最重要的环节就是要写得出递推方程,里面暗含的就是原问题和子问题之间的关系到底是什么,比如投资问题。
(1)投资问题

递推方程和边界条件 :
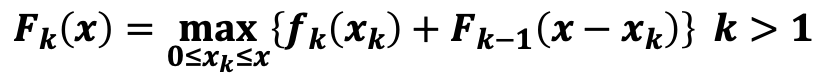
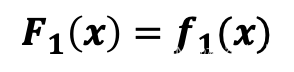
最外层这个最大,我们考虑在对第k个项目投资的时候,投多少钱剩下的钱去做前面的投资,由于 F k F_k Fk本身就是一个递归的定义,必须要给前k个项目投资的时候获得最大的收益,这就表示前k-1个项目最大的收益是多少,这样的投资组合只考虑最后一层,考虑最后那一个项目怎么投,剩下的钱交给算法来解决,去投资前面的项目,这个地方就有点像矩阵链(最后一次加括号怎么加),把最后一次加括号的位置做一个遍历,原问题自然就分解为两部分了,前面部分后面部分怎么去加呢,也不管,就丢给递归函数让它去解决,其实可以看作是阶段性的进行。
现在前k-1个项目里面投,然后再前k个项目投,投完之后,再去投资更多一点的项目数