【代数之美】奇异值分解（SVD）及其在线性最小二乘解Ax=b上的应用

奇异值分解（Singular Value Decomposition，SVD） 是线性代数中重要的矩阵分解，是特征分解在任意矩阵上的推广，在立体视觉、三维重建领域应用非常广泛。由于可以用于求解线性方程的最小二乘解，所以在求解本质矩阵、单应性矩阵、点云刚性变换矩阵时，都能用到SVD。本篇即给大家简单介绍下奇异值分解，并通过公式推导来说明其在线性最小二乘解$Ax=b$上的应用。

奇异值分解（SVD Decomposition）定义

对于任意矩阵$A\in R^{m\times n}$，存在正交矩阵$U\in R^{m\times m}$，$V\in R^{n\times n}$，以及对角矩阵$\Sigma \in R^{m\times n}$：


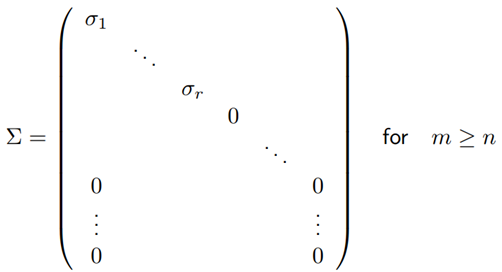
其中，对角线元素满足：
$${\sigma }_1\ge \cdots \ge {\sigma }_r\ge {\sigma }_{r+1}=\cdots ={\sigma }_{\min (m,n)}=0$$
使得，$A=U\Sigma V^T$。

此分解叫做矩阵$A$的奇异值分解（Singular Value Decomposition），是一个非常重要的矩阵分解，对角矩阵$\Sigma$的对角线元素${\sigma }_i$叫做矩阵$A$的奇异值。矩阵$U$的列向量成为左奇异向量，矩阵$V$的列向量成为右奇异向量。

使用正交矩阵$V$，可得到以下公式：
$$AV=U\Sigma$$

这可解释为，存在一组特殊的正交向量集（例如$V$的列向量集），通过矩阵$A$映射到另一组正交向量集（例如$U$的列向量集）。

SVD的一些特性

给定矩阵$A$的一组SVD分解
$$A=U\Sigma V^T$$

其中，${\sigma }_1\ge \cdots \ge {\sigma }_r\ge {\sigma }_{r+1}=\cdots ={\sigma }_{\min (m,n)}=0$

存在以下推论（$R(A)$和$N(A)$分别为矩阵$A$的值域空间和零空间）：

• $rank(A)=r$
• $R(A)=R([u_1,...u_r])$
• $N(A)=R([u_{r+1},...,u_n])$
• $R(A^T)=R([v_1,...v_r])$
• $N(A^T)=R([v_{r+1},...,v_m])$

如果我们引入
$$U_r=[u_1,...,u_r],\Sigma =diag({\sigma }_1,...,{\sigma }_r),V_r=[v_1,...,v_r]$$

则有
$$A=U_r{\Sigma }_r{V}_r^T=\sum _{i=1}^r{\sigma }_i{u}_i{v}_i^T$$
这称为矩阵$A$的二进制分解（dyadic decomposition），即将秩为$r$的矩阵$A$分解为$r$个秩为1的矩阵之和。

扫描二维码关注公众号，回复： 14144217 查看本文章

同时，可以得到
$$A^{T}A=V{\Sigma }^T\Sigma V^{T}andA{A}^T=U\Sigma {\Sigma }^T{U}^T$$

可知，奇异值的平方${\sigma }_i^2,i=1,...,p$是对称矩阵$A^{T}A$和$A{A}^T$的特征值，$v_i$和$u_i$分别是对应的特征向量。 证明如下图：

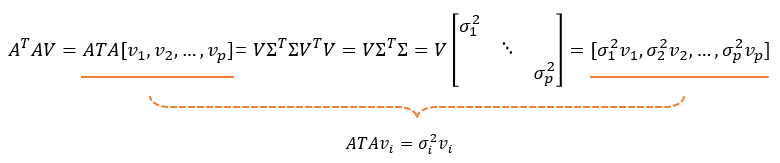
该结论很有用，我们在解$Ax=0$时，需要求$A^{T}A$的最小特征值对应的特征向量，即为SVD分解后矩阵$V$的最后一列。另一种应用场景是协方差矩阵的PCA分析时，可直接以SVD分解后的矩阵$V$各列为各方向矢量。

通过该结论，我们很容易的可以计算矩阵$A$的2-范数和Frobenius范数：
$$\begin{array}{rl}||A|{|}_2& =\sqrt{\underset{x\ne 0}{\max }\frac{||Ax|{|}_2}{||x|{|}_2}}=\sqrt{\underset{x\ne 0}{\max }\frac{x^T{A}^{T}Ax}{x^{T}x}}=\sqrt{\underset{x\ne 0}{\max }\frac{x^T{\lambda }_{A^{T}A}x}{x^{T}x}}=\sqrt{\underset{x\ne 0}{\max }{\lambda }_{A^{T}A}}={\sigma }_1\\ ||A|{|}_F& =\sqrt{\sum _{i=1}^m\sum _{j=1}^n{a}_{ij}^2}=\sqrt{trace(A^{T}A)}=\sqrt{{\sigma }_1^2+\cdots +{\sigma }_p^2}，p=\min (m,n)\end{array}$$

SVD求解线性最小二乘问题Ax=b

我们再来看SVD的经典应用：解线性方程的最小二乘解。

考虑一个线性最小二乘问题$Ax=b$：
$$\underset{x}{\min }||Ax-b|{|}_2^2$$

给定矩阵$A\in R^{m\times n}$的一组SVD分解：$A=U\Sigma V^T$

根据矩阵$U$和$V$的正交性，有
$$||Ax-b|{|}_2^2=||U^T(Ax-b)|{|}_2^2=||U^{T}Ax-U^{T}b|{|}_2^2=||\Sigma V^{T}x-U^{T}b|{|}_2^2$$

另$z=V^{T}x$，则有
$$||Ax-b|{|}_2^2=||\Sigma V^{T}x-U^{T}b|{|}_2^2=\sum _{i=1}^r({\sigma }_i{z}_i-u_i^{T}b{)}^2+\sum _{i=r+1}^m(u_i^{T}b{)}^2$$

因此，
$$\underset{x}{\min }||Ax-b|{|}_2^2=\underset{x}{\min }(\sum _{i=1}^r({\sigma }_i{z}_i-u_i^{T}b{)}^2+\sum _{i=r+1}^m(u_i^{T}b{)}^2)$$

显然，当${\sigma }_i{z}_i=u_i^{T}b$时，取最小，则最小二乘解为：
$$\begin{array}{rl}{z}_i& =\frac{u_i^{T}b}{{\sigma }_i},i=1,...,r\\ z_i& =arbitrary,i=r+1,...,n\end{array}$$

最小值为
$$\underset{x}{\min }||Ax-b|{|}_2^2=\sum _{i=r+1}^m(u_i^{T}b{)}^2$$

由$z=V^{T}x$，可得$x=Vz$，因此，通过SVD来求线性最小二乘解的公式为
$$\begin{array}{rl}x& =Vz\\ z_i& =\frac{u_i^{T}b}{{\sigma }_i},i=1,...,r\\ z_i& =arbitrary,i=r+1,...,n\end{array}$$

在上式中我们发现，当$r=n$时，有唯一最小二乘解，当$r<n$时，有无数最小二乘解，此时我们可求最小范数解：
$$\begin{array}{rl}{x}_{†}& =V{z}_{†}\\ z_i^{†}& =\frac{u_i^{T}b}{{\sigma }_i},i=1,...,r\\ z_i^{†}& =0,i=r+1,...,n\end{array}$$

我们知道最小二乘解也可通过$(A^{T}A{)}^{-1}(A^{T}b)$来求解，而通过SVD求解的优点是不需要复杂的求逆运算，且可处理$A^{T}A$为奇异阵不可逆的情况。

博主简介：
Ethan Li 李迎松（知乎：李迎松）
武汉大学 摄影测量与遥感专业博士

主方向立体匹配、三维重建

2019年获测绘科技进步一等奖（省部级）

爱三维，爱分享，爱开源
GitHub： https://github.com/ethan-li-coding
邮箱：[email protected]

个人微信：

欢迎交流！

关注博主不迷路，感谢！
博客主页：https://ethanli.blog.csdn.net