第一章的开始,作者分别用三种不同的角度解释了线性代数中最基础、最根源的组成部分——向量(Vector)。

角度一:物理专业的学生
向量是空间中的箭头,决定一个向量的是它的长度和它所指的方向。处在平面的向量是二维的,处在我们生活的空间的向量是三维的。

角度二:计算机专业的学生
向量是有序的数学列表。作者在视频中给出了房子的例子,例子中有两个维度分别是面积和价格,之所以是有序因为它们的顺序不可变换,否则失去意义。

角度三:数学家
只要保证两个向量相加以及数字和向量相乘是有意义的即可。作者在这里强调了线性代数始终围绕着这两种基础运算(Fundamental vector operation),即向量加法(Vector addition)和向量数乘(Multiplication by numbers)。
作者解释道,由于他关注的是线性代数的几何方面,所以每当引入一个关于向量的新主题时,首先需要考虑某个空间中的一个箭头,这个箭头代表一个向量。考虑这个箭头落在一个平面坐标系(x-y坐标空间)中,并且这个箭头起点位于原点(Origin),这可能与物理专业学生的看法略有不同,因为在他们眼中,向量可以在空间中自由落脚,在线性代数中,向量经常以原点作为起点。

一旦理解了“向量是空间的箭头”这种观点,就可以通过向量坐标来理解“向量是有序的数学列表”这种观点。
坐标轴的原点应该被看作整个空间的中心和所有向量的根源,一个向量的坐标由一对数构成,这对数将告诉你如何从原点(向量原点)出发到它的端点(向量终点)。

第一个数(-2)告诉你沿着x轴走多远,正数代表向右移动,负数代表向左移动;第二个数(3)告诉你在此之后沿着平行于y轴的方向走多远,正数代表向上移动,负数代表向下移动。为了把向量和点区别开来,惯用的方法是把这对数竖着写,然后用方括号括起来。(-2,3)则代表一个点。
每一对数给出唯一一个向量,而每一个向量恰好对应唯一一对数。
What about in three dimensions?
方法也是非常简单粗暴,那就再添加垂直于x轴和y轴的第三根轴,我们管它叫做z轴,这种情况下,每个向量就与一个有序三元数组对应,每一个三元数组给出唯一一个向量,而每一个向量恰好对应唯一一个三元数组。

对于更高维数的动画,这里就没有办法展示了,但是原理是一样的,大家可以自己脑补一下。
回到向量加法和向量数乘,线性代数中每一个主题都围绕着这两种运算,因此,理解它的几何含义格外重要。

向量加法(Vevtor addition):
为了把它们相加,我们平移第二个向量,使它的起点与第一个向量的终点重合,然后画一个向量,它从第一个向量的起点出发,指向第二个向量的终点,这个向量就是它们的和。
注:向量加法的意义差不多就是线性代数中唯一允许向量离开原点的情形。
为什么这样定义是合理的?
作者给出的解释是,如果你先沿着第一个向量运动,然后再按照第二个向量所描述的运动方式运动,总体效果与你沿着这两个向量的和运动无异,那么这样的定义就是合理的。
向量数乘(Multiplication by a number):
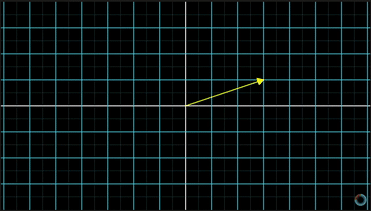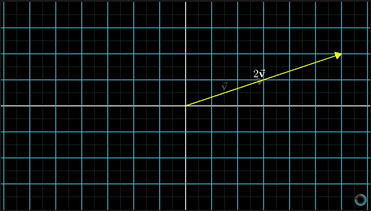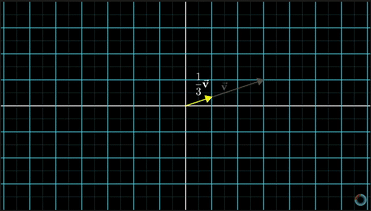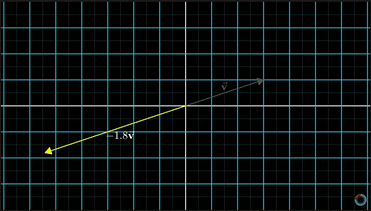
比如说有一个给定的向量,选择数字2与这个向量相乘,意味着把这个向量拉长为原来的2倍;
再比如,如果将向量乘以1/3,就意味着这个向量长度缩短为原来的1/3;
当这个向量与一个负数相乘时,比如-1.8,说明这个向量首先反向,然后伸长为原来的1.8倍。
缩放(Scaling):
这种拉伸或者压缩,有时候又使向量反向的过程被称为“缩放”。
注:从几何角度看是缩放,实际上就是数乘。
标量(Scalar):
而选择2、1/3、-1.8或者其他任何数,它们用于缩放向量,被称为“标量”。
实际上自始自终,数字在线性代数中起到的主要作用就是缩放向量,所以“标量”和“数字”两个词通常在这里可以互相转换。

转载:第一章:向量究竟是什么?