回顾Games101图形学（一）几何变换中一些公式的推导

回顾Games101 chapter 1 - 6

前言

本文只写回顾后重新加深认识的知识

透视除法的意义

经过MVP矩阵之后，将模型空间下某点的坐标，转换成了裁剪空间下的坐标，此时因为裁剪空间的范围是$x\in [-W/2，W/2]$和$y\in [-H/2，H/2]$，所以经过以下两个变换，其中除以pz就是透视除法
一：
$$\begin{gathered} -1\le 2\cdot \frac{\left(\frac{p_x}{p_z}\cdot near\right)}{w}\le 1 \\ -1\le 2\cdot \frac{\left(\frac{p_y}{p_z}\cdot near\right)}{h}\le 1 \end{gathered}$$
二：
$$\left[\begin{array}{cccc}x& y& z& w\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ \Delta x& \Delta y& \Delta z& 1\end{array}\right]=\left[\begin{array}{cccc}x+\Delta x\ast w& y+\Delta y\ast w& z+\Delta z\ast w& w\end{array}\right]$$
只有当W=1，这个三维坐标转换是等价的，才能保证位移的量是正确的，W=0时，则没有位移

只有当W=1时，三维坐标点转换成四维齐次坐标点才是等价的

坐标系变换和矩阵推导

坐标系变换理解不直观，倾向于101中闫老师所说的理解坐标系的转换通过矩阵进行的线性变换，将A坐标系下的点P，乘上矩阵得出B坐标系下的点P’，以下是抛开常见的变换（如透视投影变换、正交投影变换等）如何得出变换矩阵M，通过矩阵变换（下文着重说明）

已知坐标系A和坐标系B
$$坐标系B的x，y，z轴在坐标系A下可表示为（u_{\mathrm{x}}，u_{\mathrm{y}}，v_{\mathrm{z}}，0）$$

$$\left({\mathrm{v}}_{\mathrm{x}},{\mathrm{v}}_{\mathrm{y}},{\mathrm{v}}_{\mathrm{z}},0\right)\text{，}\left({\mathrm{w}}_{\mathrm{x}},{\mathrm{w}}_{\mathrm{y}},{\mathrm{w}}_{\mathrm{z}},0\right){\text{，坐标系B的原点在坐标系A下表示为（Q}}_{\mathrm{x}},{\mathrm{Q}}_{\mathrm{y}},{\mathrm{Q}}_{\mathrm{z}},1\text{）}$$

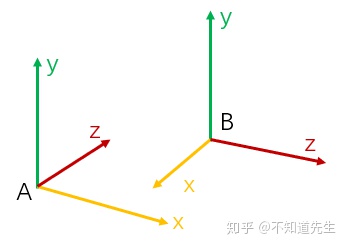
则将坐标系B中一点P从坐标系B变换到坐标系A的变换矩阵为：（注意此处的例子是将源坐标系A变换到目标坐标系B下）
$$\mathrm{M}=\left[\begin{array}{cccc}{u}_{\mathrm{x}}& u_{\mathrm{y}}& u_{\mathrm{z}}& 0\\ v_{\mathrm{x}}& v_{\mathrm{y}}& v_{\mathrm{z}}& 0\\ w_{\mathrm{x}}& w_{\mathrm{y}}& w_{\mathrm{z}}& 0\\ Q_{\mathrm{x}}& Q_{\mathrm{y}}& Q_{\mathrm{z}}& 1\end{array}\right]$$
如之前所说，变换过程中点p在空间中的绝对位置没有发生改变，只是参考坐标系发生了改变，从B坐标系变到A坐标系。（缩放，旋转，平移变换只有在同一坐标系下才有意义）

矩阵变换是基于基向量组的结果

• 矩阵变换之于同一个坐标系，可以理解为坐标系不变，点的位置改变
• 矩阵变换之于不同坐标系，可以理解为点的绝对位置不变，坐标系改变

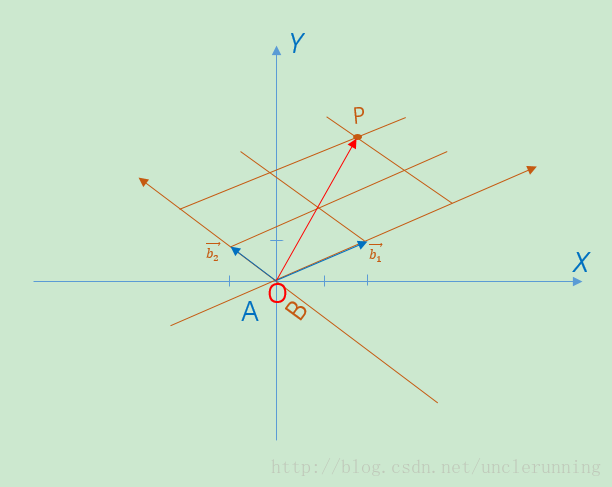
$$\left[\begin{array}{c}{x}^{{}^{\prime }}\\ y^{{}^{\prime }}\end{array}\right]=B\left[\begin{array}{c}x\\ y\end{array}\right]\Rightarrow \left[\begin{array}{c}x\\ y\end{array}\right]=B^{-1}\left[\begin{array}{c}{x}^{{}^{\prime }}\\ y^{{}^{\prime }}\end{array}\right]\text{，}B=\left[\begin{array}{cc}\overrightarrow{b_1}& \overrightarrow{b_2}\end{array}\right]\text{，且}\overrightarrow{b_1}\text{，}\overrightarrow{b_2}\text{是坐标系}B\text{的基向量}$$

其中，矩阵B的各个列向量分别对应B坐标系的各个基向量，$\left[\begin{array}{c}x\\ y\end{array}\right]$是向量$\overrightarrow{OP}$或者说点P在B坐标系的表示，$\left[\begin{array}{c}{x}^{{}^{\prime }}\\ y^{{}^{\prime }}\end{array}\right]$则是向量$\overrightarrow{OP}$或者点P在A坐标系中的表示

以图中的两个向量$\overrightarrow{b_1}$，$\overrightarrow{b_2}$为基确定一个坐标系B，显然在B坐标系中$\overrightarrow{b_{1B}}=\left[\begin{array}{c}1\\ 0\end{array}\right]$，$\overrightarrow{b_{2B}}=\left[\begin{array}{c}0\\ 1\end{array}\right]$，接下来，将$\overrightarrow{b_1}$，$\overrightarrow{b_2}$定位到A坐标系中，得到$\overrightarrow{b_{1A}}=\left[\begin{array}{c}2\\ 1\end{array}\right]$，$\overrightarrow{b_{2A}}=\left[\begin{array}{c}-1\\ 1\end{array}\right]$

$\because \overrightarrow{OP}=2\overrightarrow{b_1}+2\overrightarrow{b_2}$

$\therefore \overrightarrow{OP}$在B坐标系中的表示为$\left[\begin{array}{c}2\\ 2\end{array}\right]$，现在，将$\overrightarrow{OP}$用A坐标系描叙：
$\overrightarrow{OP}=2\overrightarrow{b_1}+2\overrightarrow{b_2}=2\overrightarrow{b_{1A}}+2\overrightarrow{b_{2A}}=\left[\begin{array}{cc}\overrightarrow{b_{1A}}& \overrightarrow{b_{2A}}\end{array}\right]\left[\begin{array}{c}2\\ 2\end{array}\right]=\left[\begin{array}{c}2\\ 4\end{array}\right]$
现在，令矩阵B=$\left[\begin{array}{cc}\overrightarrow{b_{1A}}& \overrightarrow{b_{2A}}\end{array}\right]$，P点是用B坐标系表示的任意一点$(x,y)$。
于是$\overrightarrow{OP}$在A坐标系中的表示$\left[\begin{array}{c}{}^{x^{{}^{\prime }}}\\ y^{{}^{\prime }}\end{array}\right]=B\left[\begin{array}{c}x\\ y\end{array}\right]$，显然，B是可逆的，于是就有了之前的结论
那么在这个例子当中，当我们需要知道某点在转换坐标系后的新坐标时，通过该例子也可以加深印象，比如在B坐标系下有点$Q(3,4)$，即$\overrightarrow{OQ}=(3,4)$，跟据刚才的例子可以看出它转换在A坐标系下的点
$$\overrightarrow{OQ}=2\overrightarrow{b_1}+2\overrightarrow{b_2}=2\overrightarrow{b_{1A}}+2\overrightarrow{b_{2A}}=\left[\begin{array}{cc}\overrightarrow{b_{1A}}& \overrightarrow{b_{2A}}\end{array}\right]\left[\begin{array}{c}3\\ 4\end{array}\right]=\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]\left[\begin{array}{c}5\\ 4\end{array}\right]=\left[\begin{array}{c}6\\ 9\end{array}\right]$$

即转换到A坐标系下的点$Q^{{}^{\prime }}$的坐标为$Q^{{}^{\prime }}(6,9)$

虽然这里的讨论是基于二维的，但是，结论可以扩展到任意维度

阐述结论：

将B坐标系的基向量定位到A坐标系，然后将定位之后的基向量作为矩阵B的列向量，用矩阵B对B坐标系中的点P的坐标进行矩阵变换，将得到点P在A坐标系中的坐标。这个过程，就是从坐标系 B到坐标系A的一个追溯过程

View/Camera Transformation

先将相机移到原点，然后进行分别对坐标轴进行旋转，用矩阵表示则是$M_{view}=R_{view}{T}_{view}$

• 将相机移回原点

$$T_{view}=\left[\begin{array}{cccc}1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\end{array}\right]$$

• $Rotategto-Z,ttoY,\left(g\times t\right)ToX$
  g是相机看的方向（lookAt），t是相机向上的方向（Up），也就是相机的-Z轴和Y轴，两个向量叉积就是另一个坐标轴

$$R_{view}^{-1}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_t& x_{-g}& 0\\ y_{\hat{g}\times \hat{t}}& y_t& y_{-g}& 0\\ z_{\hat{g}\times \hat{t}}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$$

旋转矩阵是正交矩阵，所以旋转矩阵的逆就是旋转矩阵的转置

$$R_{view}^{}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ x_t& y_t& y_t& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$$

正交投影矩阵

无论是正交投影还是透视投影，都是要将x、y、z移到-1到1的范围内，先将中心点移到原点，然后缩放
$$M_{ortho}=\left(\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right)$$

透视投影矩阵推导

首先先将frustum 转变为cuboid（n -> n,f -> f）($M_{persp->ortho}$)
然后再做正交投影

整个投影变换包括两部分

• $v=P（矩阵）\ast p$
• $v=\frac{v}{v_w}=\frac{v}{pz}$透视除法

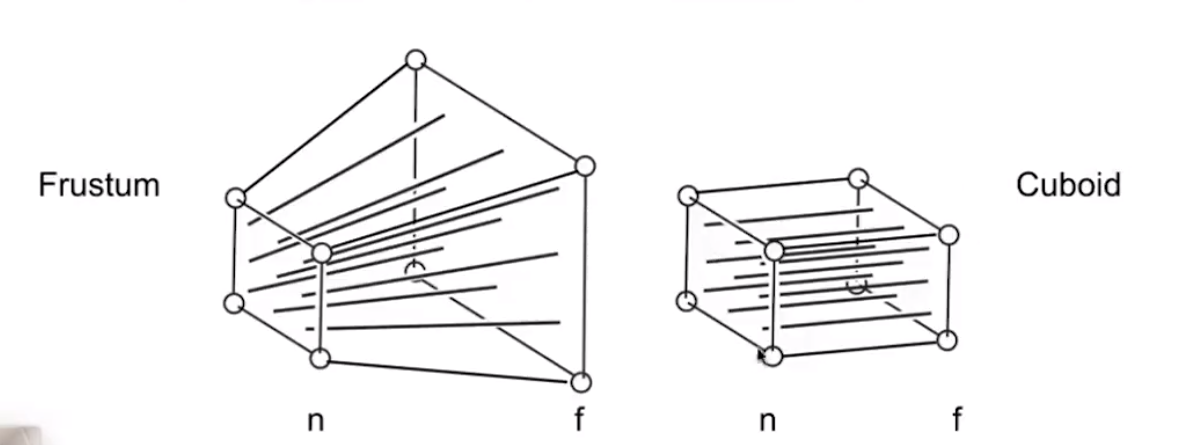
以上大概推出等式这一步，接下来用公式展示更为直观
$$\left(\begin{array}{cccc}m00& m01& m02& m03\\ m10& m11& m12& m13\\ m20& m21& m22& m23\\ m30& m31& m32& m33\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}\frac{x}{z\ast aspect\ast \tan \left(\frac{fov}{2}\right)}\\ \frac{y}{z\ast tan\left(\frac{fov}{2}\right)}\\ z^{‘’}\\ 1\end{array}\right)$$

$$m00\ast x+m01\ast y+m02\ast z+m03=\frac{x}{z\ast aspect\ast \tan \left(\frac{fov}{2}\right)}$$

将右边的四维列向量表示的坐标每一项乘以z，所以有

$$\left(\begin{array}{cccc}m00& m01& m02& m03\\ m10& m11& m12& m13\\ m20& m21& m22& m23\\ m30& m31& m32& m33\end{array}\right)\ast \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}\frac{x}{aspect\ast \tan \left(\frac{fov}{2}\right)}\\ \frac{y}{\tan \left(\frac{fov}{2}\right)}\\ z\ast z^{{}^{\prime }{}^{\prime }}\\ z\end{array}\right)$$

所以求得矩阵为
$$\left(\begin{array}{cccc}\frac{1}{aspect\ast \tan \left(\frac{fov}{2}\right)}& 0& 0& 0\\ 0& \frac{1}{\tan \left(\frac{fov}{2}\right)}& 0& 0\\ 0& 0& m22& m23\\ 0& 0& 1& 0\end{array}\right)$$

$$\begin{gathered} m22\ast z+m23=z\ast z^{{}^{\prime }{}^{\prime }} \\ \Rightarrow m22+\frac{m23}{z}=z^{{}^{\prime }{}^{\prime }} \end{gathered}$$

因为z=zNear时，z’’=-1；z=zFar时，z’’=1所以有以下等式
$$\begin{gathered} m22+\frac{m23}{zNear}=-1 \\ m22+\frac{m23}{zFar}=1 \end{gathered}$$
联立求得：
$$\begin{gathered} m22=\frac{-zFar-zNear}{zNear-zFar} \\ m23=\frac{2\ast zFar\ast zNear}{zNear-zFar} \end{gathered}$$
最后求得投影矩阵为
$$\left(\begin{array}{cccc}\frac{1}{aspect\ast \tan \left(\frac{fov}{2}\right)}& 0& 0& 0\\ 0& \frac{1}{\tan \left(\frac{fov}{2}\right)}& 0& 0\\ 0& 0& \frac{-zFar-zNear}{zNear-zFar}& \frac{2\ast zNear\ast zFar}{zNear-zFar}\\ 0& 0& 1& 0\end{array}\right)$$
将这样得矩阵乘以视锥体内的一个顶点坐标，得到一个新的向量，再将这个向量的每个分量除以第四个分量（此步骤也被称为透视除法）（w），这样就可以得到顶点映射到规则立方观察体后的新的坐标

注意：z坐标的映射方式的获得，最后我们是为了方便矩阵乘法的操作方向求得了z坐标与cvv中的z坐标的映射方式：
$$m22+\frac{m23}{z}=z^{{}^{\prime }{}^{\prime }}$$
此时的映射并不是线性的，当z越大时，z的变化对z’'的扰动越小

Canonical Cube to Screen

• Irrelevant to z
• Transform in xy plane : [-1, 1] to [0, width] × [0, height]
• Viewport transform matrix:

视口矩阵
$$M_{viewport}=\left[\begin{array}{cccc}\frac{width}{2}& 0& 0& \frac{width}{2}\\ 0& \frac{height}{2}& 0& \frac{height}{2}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

深度z的计算

前言
3D光栅化发生在图元被变换到Screen space之后，因为这里的Screen space与2D的Screen Space完全一致，所以2D的光栅化算法在这里依然适用。

然而由于图元经过了投影变换，且投影变换为非线性变换，所以不能用简单的线性插值获取fragment的属性

投影变换不会保持相对距离不变性

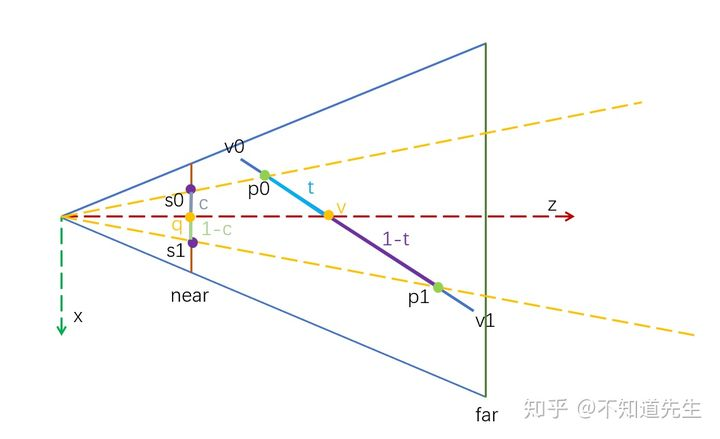
如上图所示，view space中的线段v0v1上两点$p0\left(p{0}_x,p{0}_y,p{0}_z,1\right)$，$p1\left(p{1}_x,p{1}_y,p{1}_z,1\right)$在near plane上的投影为点$s0\left(s{0}_x,s{0}_y\right)$，$s1\left(s{1}_x,s{1}_y\right)$。$p0$，$p1$中间一点$v(v_x,v_y,v_z,1)$在near plane上的投影为点$q(q_x,q_y)$。从图中可以看出点v到p0，p1的距离比值与点q到s0，s1的距离比值完全不同，投影变换不保持距离不变。

为了执行z-buffer算法，需要通过点q获取到v的深度值(z)
点$v$的深度值可以通过如下方法插值得到：

$$v_z=\frac{1}{\frac{c}{p{1}_z}+\frac{\left(1-c\right)}{p{0}_z}}$$

以下是推导的过程：

手写版：

文字版：
由于点$q$为点$v$在near plane上的投影，因此点$q$与点$v$的关系为：

• $q_x=\frac{v_x\cdot near}{v_z}$
  且$v$位于$p0p1$之间，则
• $v_z=p{0}_z+t\cdot (p{1}_z-p{0}_z)=\frac{v_x\cdot near}{q_x}$
  由点$v$在$p0$，$p1$之间，点$q$在$s0$，$s1$之间则有
• $v_x=p{0}_x\cdot (1-t)+p{1}_x\cdot t=p{0}_x+t\cdot (p{1}_x-p{0}_x)$
• $q_x=s{0}_x\cdot (1-c)+s{1}_x\cdot c=s{0}_x+c\cdot (s{1}_x-s{0}_x)$
  代入式(1)可得
  $v_z=\frac{v_x\cdot near}{q_x}=\frac{(p{0}_x+t\cdot (p{1}_x-p{0}_x))\cdot near}{s{0}_x+c\cdot (s{1}_x-s{0}_x)}$式(2)
  又s0和s1分别为p0和p1在near plane上的投影，则：
• $s{0}_x=\frac{p{0}_x\cdot near}{p{1}_z}$
• $s{1}_x=\frac{p{1}_x\cdot near}{p{1}_z}$
  代入式(2)可得：

$$v_z=\frac{\left(\frac{p{0}_x\cdot s{0}_x}{near}+t\cdot \left(\frac{p{1}_x\cdot s{1}_x}{near}-\frac{p{0}_x\cdot s{0}_x}{near}\right)\right)\cdot near}{s{0}_x+c\cdot \left(s{1}_x-s{0}_x\right)}$$

$$\begin{gathered} v_z=\frac{\left(\frac{p{0}_x\cdot s{0}_x}{near}+t\cdot \left(\frac{p{1}_x\cdot s{1}_x}{near}-\frac{p{0}_x\cdot s{0}_x}{near}\right)\right)\cdot near}{s{0}_x+c\cdot \left(s{1}_x-s{0}_x\right)} \\ {v}_z=\frac{\left(p{0}_x\cdot s{0}_x+t\cdot \left(p{1}_x\cdot s{1}_x-p{0}_x\cdot s{0}_x\right)\right)}{s{0}_x+c\cdot \left(s{1}_x-s{0}_x\right)} \\ p{0}_z+t\cdot \left(p{1}_z-p{0}_z\right)=\frac{\left(p{0}_x\cdot s{0}_x+t\cdot \left(p{1}_x\cdot s{1}_x-p{0}_x\cdot s{0}_x\right)\right)}{s{0}_x+c\cdot \left(s{1}_x-s{0}_x\right)} \\ \left(p{0}_z+t\cdot \left(p{1}_z-p{0}_z\right)\right)\cdot \left(s{0}_x+c\cdot \left(s{1}_x-s{0}_x\right)\right)=p{0}_x\cdot s{0}_x+t\cdot \left(p{1}_x\cdot s{1}_x-p{0}_x\cdot s{0}_x\right) \\ p{0}_z\cdot s{0}_x+p{0}_z\cdot c\cdot \left(s{1}_x-s{0}_x\right)+t\cdot \left(p{1}_z-p{0}_z\right)\cdot s{0}_x+t\cdot c\cdot \left(p{1}_z-p{0}_z\right)\cdot \left(s{1}_x-s{0}_x\right)=p{0}_x\cdot s{0}_x+t\cdot \left(p{1}_x\cdot s{1}_x-p{0}_x\cdot s{0}_x\right) \end{gathered}$$

化简得：
$$t\cdot \left(p{1}_z-c\cdot \left(p{1}_z-p{0}_z\right)\right)=c\cdot p{0}_z$$
则：
$$t=\frac{c\cdot p{0}_z}{c\cdot p{0}_z+(1-c)\cdot p{1}_z}$$
代入式(1)可得
$$v_z=p{0}_z+t\cdot (p{1}_z-p{0}_z)$$
$$v_z=p{0}_z+\frac{c\cdot p{0}_z}{c\cdot p{0}_z+(1-c)\cdot p{1}_z}\cdot (p{1}_z-p{0}_z)$$
$$v_z=\frac{1}{\frac{c}{p{1}_z}+\frac{(1-c)}{p{0}_z}}$$

若View Space中三角形$v0v1v2$，变换到Screen Space后为三角形$s0s1s2$，$v0v1v2$内一点v在Screen Space的投影点$s0s1s2$内的点$q$，对三角形$s0s1s2$内的点（fragment）$q$，可以通过如下方法取得fragment$q$在View Space中对应的深度值：

$$q.z=v.z=\frac{1}{\frac{\lambda 0}{v0.z}+\frac{\lambda 1}{v1.z}+\frac{\lambda 2}{v2.z}}$$

$\lambda 0,\lambda 1,\lambda 2$为点p在三角形$s0s1s2$内的重心坐标
引入结论：
对Screen Space三角形$s0,s1,s2$内一点$p$的任意属性插值的公式为:
$$Atribute\left(p\right)=z\cdot \left(\frac{\lambda 0\cdot Atribute\left(v0\right)}{z0}+\frac{\lambda 1\cdot Atribute\left(v1\right)}{z1}+\frac{\lambda 2\cdot Atribute\left(v2\right)}{z2}\right)$$
$\lambda 0,\lambda 1,\lambda 2$为点$p$的重心坐标，$z0,z1,z2,z$分别为$s0,s1,s2,p$在view space中对应点的深度值，可以用这个方法插值得到$p$在NDC Space内对应点的深度值
此处贴一下Games101作业框架中关于深度的计算，与上述公式对应$z=z_{i}nterpolated\ast w_{r}eciprocal$

    auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
    float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
    float z_interpolated =
    alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
    z_interpolated *= w_reciprocal;

    if (depth_buf[get_index(x, y)] > z_interpolated) {
    
    
        depth_buf[get_index(x, y)] = z_interpolated;
        Eigen::Vector3f point;
        point << static_cast<float>(x), static_cast<float>(y), z_interpolated;
        set_pixel(point, t.getColor());
    }

罗德里格斯旋转公式

指定任意轴k旋转$\alpha$角得出旋转矩阵
字写得不好，在爬了…
手写版：

文字版：
首先先将$\overrightarrow{k}$处理成单位向量，这点很重要，关乎着下一步等式是否成立，有些博文写这里不需要处理单位向量，这是错的

$$\overrightarrow{v}\cdot \overrightarrow{k}=|\overrightarrow{v}|\cdot |\overrightarrow{k}|\cdot \cos <\overrightarrow{v}\text{,}\overrightarrow{k}>=|\overrightarrow{v}|\cdot \cos <\overrightarrow{v}\text{,}\overrightarrow{k}>$$
可得
$$\begin{gathered} \overrightarrow{v_{||}}=|\overrightarrow{v}|\cdot \cos <\overrightarrow{v},\overrightarrow{k}>\cdot \overrightarrow{k} \\ \overrightarrow{v}=\overrightarrow{v_{\perp }}+\overrightarrow{v_{||}} \\ \overrightarrow{v_{\perp }}=\overrightarrow{v}-\overrightarrow{v_{||}}=\overrightarrow{v}-\left(\overrightarrow{v}\cdot \overrightarrow{k}\right)\overrightarrow{k} \end{gathered}$$
绕$\overrightarrow{k}$做旋转时，向下做垂线，可看作底部经过了类似半圆的旋转
要求得$\overrightarrow{v_{rot}}=\overrightarrow{v_{||}}+\overrightarrow{v_{rot\perp }}$，将$\overrightarrow{v_{rot\perp }}$作正交分解有$\overrightarrow{v_{rot\perp }}=\overrightarrow{a}+\overrightarrow{b}$，易得$|\overrightarrow{w}|=|\overrightarrow{v_{\perp }}|$，则有$\overrightarrow{w}=\overrightarrow{k}\times \overrightarrow{v_{\perp }}=\overrightarrow{k}\times \left[\overrightarrow{v}-\overrightarrow{v_{||}}\right]=\overrightarrow{k}\times \overrightarrow{v}-\overrightarrow{k}\times \overrightarrow{v_{||}}=\overrightarrow{k}\times \overrightarrow{v}-0=\overrightarrow{k}\times \overrightarrow{v}$
接下来求$\overrightarrow{a}$和$\overrightarrow{b}$

$$\begin{gathered} |\overrightarrow{a}|=|\overrightarrow{v_{rot\perp }}|\cdot \cos \left(\theta -90\right)=|\overrightarrow{v_{rot\perp }}|\cdot \sin \left(\theta \right) \\ \overrightarrow{a}=\frac{\overrightarrow{w}}{|\overrightarrow{w}|}\cdot |\overrightarrow{a}|=\frac{\overrightarrow{w}}{|\overrightarrow{v_{rot\perp }}|}\cdot |\overrightarrow{v_{rot\perp }}|\cdot \sin \left(\theta \right)=\overrightarrow{w}\cdot \sin \left(\theta \right) \end{gathered}$$

$$\begin{gathered} |\overrightarrow{b}|=|\overrightarrow{v_{rot\perp }}|\cdot \cos \left(180-\theta \right)=|\overrightarrow{v_{rot\perp }}|\cdot \cos \left(\theta \right) \\ \overrightarrow{b}=\frac{\overrightarrow{v_{\perp }}}{|\overrightarrow{v_{\perp }}|}\cdot |\overrightarrow{b}|=\frac{\overrightarrow{v_{\perp }}}{|\overrightarrow{v_{\perp }}|}\cdot |\overrightarrow{v_{rot\perp }}|\cdot \cos \left(\theta \right)=\overrightarrow{v_{\perp }}\cdot \cos \left(\theta \right)\text{注意}|\overrightarrow{v_{\perp }}|=|\overrightarrow{v_{rot\perp }}| \end{gathered}$$

$$\begin{gathered} \overrightarrow{v_{rot\perp }}=\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{w}\cdot \sin \left(\theta \right)+\overrightarrow{v_{\perp }}\cdot \cos \left(\theta \right)=\sin \left(\theta \right)\cdot \left(\overrightarrow{k}\times \overrightarrow{v}\right)+\cos \left(\theta \right)\left(\overrightarrow{v}-\left(\overrightarrow{v}\cdot \overrightarrow{k}\right)\overrightarrow{k}\right) \\ \overrightarrow{v_{rot}}=\overrightarrow{v_{||}}+\overrightarrow{v_{rot\perp }}=\left(\overrightarrow{v}\cdot \overrightarrow{k}\right)\overrightarrow{k}+\sin \left(\theta \right)\cdot \left(\overrightarrow{k}\times \overrightarrow{v}\right)+\cos \left(\theta \right)\left(\overrightarrow{v}-\left(\overrightarrow{v}\cdot \overrightarrow{k}\right)\overrightarrow{k}\right) \\ =\cos \left(\theta \right)\overrightarrow{v}+\left(1-\cos \left(\theta \right)\left(\overrightarrow{v}\cdot \overrightarrow{k}\right)\overrightarrow{k}\right)+\sin \left(\theta \right)\cdot \left(\overrightarrow{k}\times \overrightarrow{v}\right) \end{gathered}$$

把$\overrightarrow{k}$和$\overrightarrow{v}$分别写为列向量
$$\overrightarrow{k}=\left(\begin{array}{c}{k}_x\\ k_y\\ k_z\end{array}\right)$$

$$\overrightarrow{v}=\left(\begin{array}{c}{v}_x\\ v_y\\ v_z\end{array}\right)$$

令$\overrightarrow{v_{rot}}=R\cdot \overrightarrow{v}$
两个式子
$$\left(\overrightarrow{v}\cdot \overrightarrow{k}\right)\overrightarrow{k}=\overrightarrow{k}\left(\overrightarrow{v}\cdot \overrightarrow{k}\right)=\overrightarrow{k}\left(\overrightarrow{k^T}\cdot \overrightarrow{v}\right)$$
$$\overrightarrow{k}\times \overrightarrow{v}=\left[\begin{array}{c}{k}_y{v}_z-k_z{v}_y\\ k_z{v}_x-k_x{v}_z\\ k_x{v}_y-k_y{v}_x\end{array}\right]=\left[\begin{array}{ccc}0& -k_z& k_y\\ k_z& 0& -k_x\\ -k_y& k_x& 0\end{array}\right]\left[\begin{array}{c}{v}_x\\ v_y\\ v_z\end{array}\right]$$
结合以上两个式子可得,其中$I$为3×3的单位矩阵
$$R=I\cos \left(\theta \right)+\left(1-\cos \left(\theta \right)\right)\left(\begin{array}{c}{k}_x\\ k_y\\ k_z\end{array}\right)\left(\begin{array}{ccc}{k}_x& k_y& k_z\end{array}\right)+\sin \left(\theta \right)\left(\begin{array}{ccc}0& -k_z& k_y\\ k_z& 0& -k_x\\ -k_y& k_x& 0\end{array}\right)$$
以下是比较通用的表示方式
$$R\left(n,\alpha \right)=\cos \left(\alpha \right)I+\left(1-\cos \left(\alpha \right)\right)n{n}^T+\sin \left(\alpha \right)\left(\begin{array}{ccc}0& -n_z& n_y\\ n_z& 0& -n_x\\ -n_y& n_x& 0\end{array}\right)$$

部分引用的博文

https://blog.csdn.net/unclerunning/article/details/70948696#%E9%BD%90%E6%AC%A1%E5%9D%90%E6%A0%87%E7%B3%BB%E4%B8%8E%E5%B9%B3%E7%A7%BB

https://zhuanlan.zhihu.com/p/45757899