非线性最小二乘拟合
本章描述多维非线性最小二乘拟合的函数。求解非线性最小二乘问题一般有两类算法,即行搜索法和信赖域法。GSL目前只实现信赖域法,并为用户提供对迭代中间步骤的完全访问。用户还能够调优一些参数,这些参数会影响算法的底层参数,有助于加快当前特定问题的收敛速度。GSL为非线性最小二乘拟合提供了两个独立的接口。第一个是为小到中等规模的问题设计的,第二个是为非常大的问题设计的,这些问题可能有也可能没有显著的稀疏结构。
头文件gsl_multifit_nlinear.h包含多维非线性拟合函数的原型,以及与小型到中型系统相关的声明。
头文件gsl_multilarge_nlinear.h包含多维非线性拟合函数的原型,以及与大型系统相关的声明。
41.1 概述
多维非线性最小二乘拟合问题需要n个函数平方残差的最小值,fi,在p参数,xi,
![]()
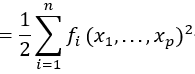
在信赖域法中,目标(或成本)函数Φ(x)用模型函数mk(δ)在某一点xk附近近似。模型函数通常是简单的围绕点xk的二阶泰勒级数展开,即:
![]()
其中,![]() 是点xk 上的梯度向量,Bk=∇2Φ(xk) 是xk 上的Hessian矩阵,或者是它的某种近似,而J是n乘p的雅可比矩阵
是点xk 上的梯度向量,Bk=∇2Φ(xk) 是xk 上的Hessian矩阵,或者是它的某种近似,而J是n乘p的雅可比矩阵
![]()
为了找到下一步δ ,我们将模型函数mk(δ)最小化,但是只在我们相信mk(δ)是目标函数Φ(xk +δ)的很好的近似的区域内寻找解决方案。换句话说,我们寻求信赖域子问题(TRS)的一个解。
![]()
其中,∆k > 0为信任域半径,Dk为比例矩阵。如果Dk= I,则信赖域是一个以xk为中心半径∆k的球。在某些应用中,参数向量x可能有很大不同的比例。例如,参数可能是103 K量级的温度,而另一个参数可能是10-6 m量级的长度。在这种情况下,球形信任区域可能不是最佳选择,因为如果Φ沿着一个尺度的方向快速变化,而沿着不同尺度的方向变化更慢,那么模型函数mk在Φ沿着快速变化的方向,可能没有很好的近似。在这类问题中,最好使用一个椭圆信赖域,将Dk设置为一个对角矩阵,其元素的设计使比例步长Dkδ具有近似相同数量级的元素。
上述信赖域子问题,通常相当于求解一个线性最小二乘系统(或多个系统)的步长δ。一旦计算了δ,就检查它是否减少了目标函数Φ(x)。一个有用的统计数据是看比率,
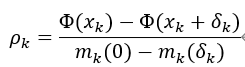
其中,分子是由于步进δk 引起的目标函数的实际减少量,分母是由于模型mk引起的预测减少量。如果ρk为负,则意味着步进δk 增加了目标函数值,因此被拒绝。如果ρk是正的,那么我们找到了一个简化目标函数的步骤,它被接受了。此外,如果ρk接近于1,则说明模型函数在信赖域内很好地逼近目标函数,以此,在下一次迭代中,信赖域被扩大,以便采取更大胆的步骤。当一个步进被拒绝时,信任区域被缩小,TRS被再次求解。现在可以给出GSL所使用的一般信赖域法的大致过程。
信赖域法
1. 初始化:给定x0,构造m0(δ), D0和∆0>0
2. 当k = 0,1,2,…
a. 如果收敛,则停止
b. 求解试验步长δk的TRS
c. 通过计算ρk来计算试验步长
1). 如果接受步长,则设xk+1= xk+δk,增加半径∆k+1 = α∆k
2). 如果拒绝步长,设xk+1 = xk,减小半径∆k+1 = ∆kβ ;转到2 (b)
d. 构造mk+1(δ)和Dk+1
GSL为用户提供了求解2(b)中信赖域子问题的一系列不同的算法,也包括不同的比例矩阵Dk的选择和不同的信赖域半径∆k的更新方法。因此,在提供合理的默认方法的同时,用户可以根据自己的具体问题调整算法的各个步骤。
41.2 信赖域子问题(TRS)的求解
下面我们描述求解信赖域子问题的可行方法。可用的方法提供了信赖域子问题的精确或近似解。在下面的所有算法中,Hessian矩阵Bk 近似为Bk≈JkTJk ,其中Jk=J(xk) 。在所有的方法中,TRS的解涉及到求解一个包含雅可比矩阵的线性最小二乘系统。对于小到中等规模的问题(gsl_multifit_linear接口),这是通过将用户提供的完整雅可比矩阵分解为Cholesky、QR或SVD分解来实现的。对于大型系统(gsl_multilarge_nlinear接口),用户有两个选择。一种是迭代求解系统,而不需要将整个雅可比矩阵存储在内存中。使用这种方法,用户必须提供一个程序来计算给定向量u的矩阵向量乘积Ju或JTu。这种迭代方法对于雅可比矩阵具有稀疏结构的系统特别有用,因此形成矩阵向量乘积的成本很低。对于大型系统,第二种选择包括形成正规方程矩阵JTJ,然后使用Cholesky分解分解它。标准方程矩阵是p乘p,通常比完整的n乘p雅可比矩阵小得多,并且即使完整的Jacobian矩阵不能,通常也可以将其存储在内存中。对于大型、密集的系统,或者迭代方法难以收敛时,这个选项是有用的。
41.2.1 Levenberg-Marquardt
有定理表明,如果δk 是上述信赖域子问题的一个解,则存在µk≥0使,
![]()
用μk(∆k-||Dkδk||)=0 。这构成了Levenberg-Marquardt算法的基础,该算法通过调整参数μk 而不是直接调整半径∆k 来控制信任区域的大小。对于每个半径∆k ,有一个唯一的参数μk 求解TRS,它们之间呈反比关系,大的μk 对应较小的信任区域,小的μk 对应较大的信任区域。
在每次迭代逼近Bk≈JkTJk 的情况下,为了计算步长δk ,求解以下线性最小二乘问题:
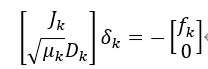
如果接受步长δk ,则在下一次迭代中减少μk ,以获得更大的步长,否则增加μk ,以获得更小的步长。Levenberg-Marquardt算法提供了信赖域子问题的精确解,但通常每次迭代的计算代价比下面讨论的近似方法更高,因为它可能需要对不同的μk 值求解多次以上的最小二乘系统。
41.2.2 带有测地线加速度的Levenberg-Marquardt
本方法对标准Levenberg-Marquardt步长δk 应用了所谓的测地加速度修正(Transtrum等,2011)。通过将δk 解释为模型参数空间中沿测地线的一级步长(即速度δk=vk ),测地线加速度ak 是沿测地线的二阶修正,这是通过求解线性最小二乘系统确定的。
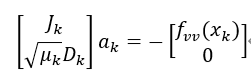
式中,fvv 是残差向量在速度v 方向上的二阶方向导数,fvv(x)=Dv2f=αβvαvβ∂α∂βf(x) ,其中α和β对p参数求和。新的总步长是δk'=vk+12ak 。二阶修正ak 可以用适当的附加成本计算出来,并且已经被证明可以显著减少迭代次数(和昂贵的雅可比矩阵计算),从而在各种不同的问题上达到收敛。为了利用测地加速度,用户必须提供一个函数,该函数提供第二个方向导数矢量fvv(x) ,或者,用函数f(x + hv)在本库使用限差分方法来估计这个向量,其中h是可调的步长(参见h_fvv参数描述)。
41.2.3 狗腿法
这是Powell的狗腿方法,它通过将搜索限制在一个分段线性“狗腿”路径上,找到信赖域子问题的近似解,该路径由原点、沿最陡下降方向代表模型最小化的Cauchy点和高斯-牛顿点组成,这是无约束模型的总体最小值。用求解的方法计算高斯-牛顿步长。
![]()
这是每个迭代的主要计算任务,但每个迭代只需要执行一次。如果高斯-牛顿点在信任区域内,则选择它作为步长。如果它在外部,那么该方法计算位于梯度方向的柯西点。如果柯西点也在信任区域之外,该方法假定它仍然远离最小值,然后沿着梯度方向继续,截断信任区域边界处的步长。如果柯西点在信赖域内,高斯-牛顿点在信赖域外,该方法采用狗腿步长,它是梯度方向和高斯-牛顿方向的线性组合,停在信赖域边界处。
41.2.4 双狗腿
本方法是对经典的狗腿算法的改进,算法试图在迭代距离最小值还很远的情况下包含关于高斯-牛顿步长的信息。当柯西点在信赖域内,高斯-牛顿点在信赖域外时,该方法计算一个缩放后的高斯-牛顿点,然后在柯西点和缩放后的高斯-牛顿点之间走一个狗腿步长。计算缩放比例以确保模型mk的减少量与柯西点提供的减少量大致相同。
41.2.5 二维子空间
狗腿方法将搜索TRS解限制在由柯西点和高斯-牛顿点定义的一维曲线上。改进的方法是利用柯西和高斯-牛顿方向的全二维子空间来寻找解。狗腿路径当然是在这个子空间内,所以这个方法解决的TRS至少与狗腿方法一样准确。该方法是搜索更大的子空间来寻找解,因此在某些问题上它比狗腿算法收敛更快。由于子空间只有二维,该方法非常有效,每次迭代的主要计算是确定高斯-牛顿点。
41.2.6 Steihaug-Toint共轭梯度
狗腿法的难点之一是计算雅可比矩阵奇异时的高斯-牛顿步长。Steihaug-Toint方法也计算广义狗腿步,但避免了直接求解高斯-牛顿步长,而是使用迭代共轭梯度算法。该方法在雅可比矩阵奇异点处表现良好,也适用于雅可比矩阵分解代价高昂的大规模问题。
41.3 加权非线性最小二乘法
加权非线性最小二乘拟合使函数最小化
![]()

其中W=diag(w1,w2,…,wn)为权重矩阵,||f||W2=fTWf 。权重wi 通常定义为wi=1/δi2 ,其中δi 为第i次测量的误差。简单的变量变换f=W12f 生成Φ(x)=12||f||2 ,其形式与未加权情况相同。用户可以直接对其函数残差和雅可比矩阵执行此转换,也可以使用gsl_multifit_nlinear_winit()接口自动执行正确的缩放。手动进行这个变换,残差和雅可比矩阵需要根据公式进行修改,
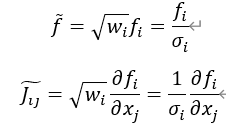
对于大型系统,用户必须执行自己的权重。