计算理论基础-1-FA有穷自动机与Pumping_Lemma泵定理

学习资料：

https://www.cnblogs.com/Bubgit/p/10240790.html

https://blog.csdn.net/shulianghan/article/details/111393044

https://www.cnblogs.com/raicho/p/11762837.html

https://blog.csdn.net/elice_/article/details/80550413

https://baike.baidu.com/item/泵引理/9490334?fr=aladdin

https://blog.csdn.net/zxbdsg/article/details/112424714

一、正则表达式与状态转移图

正则表达式

正则操作：

1.$\cdot$ 表示连接(可省略)

例： $abc\cdot 123=abc123$

2.$\mid$ 表示或

例： $abc\mid 123=\{\begin{array}{l}abc\\ 123\end{array}$

3.$\ast$ 运算start

$st{r}^i=\{\begin{array}{ll}\epsilon & i=0\\ st{r}^{i-1}\cdot str& i>=1\end{array}$

其中$\epsilon$指空串

例： { 0 , 1 } ∗ = { ε } ∪ { 0 , 1 } ∪ { 00 , 01 , 10 , 11 } . . . \{0,1\}^* = \{\varepsilon\} \cup \{0,1\} \cup \{00,01,10,11\} ... { 0,1}∗={ ε}∪{ 0,1}∪{ 00,01,10,11}...

计算优先级

有小括号先算小括号， $\ast >\cdot >|$

状态转移图

状态转移图中，节点表示状态，边表示输入字母，双圈表示终态

正则表达式转换为状态转移图：

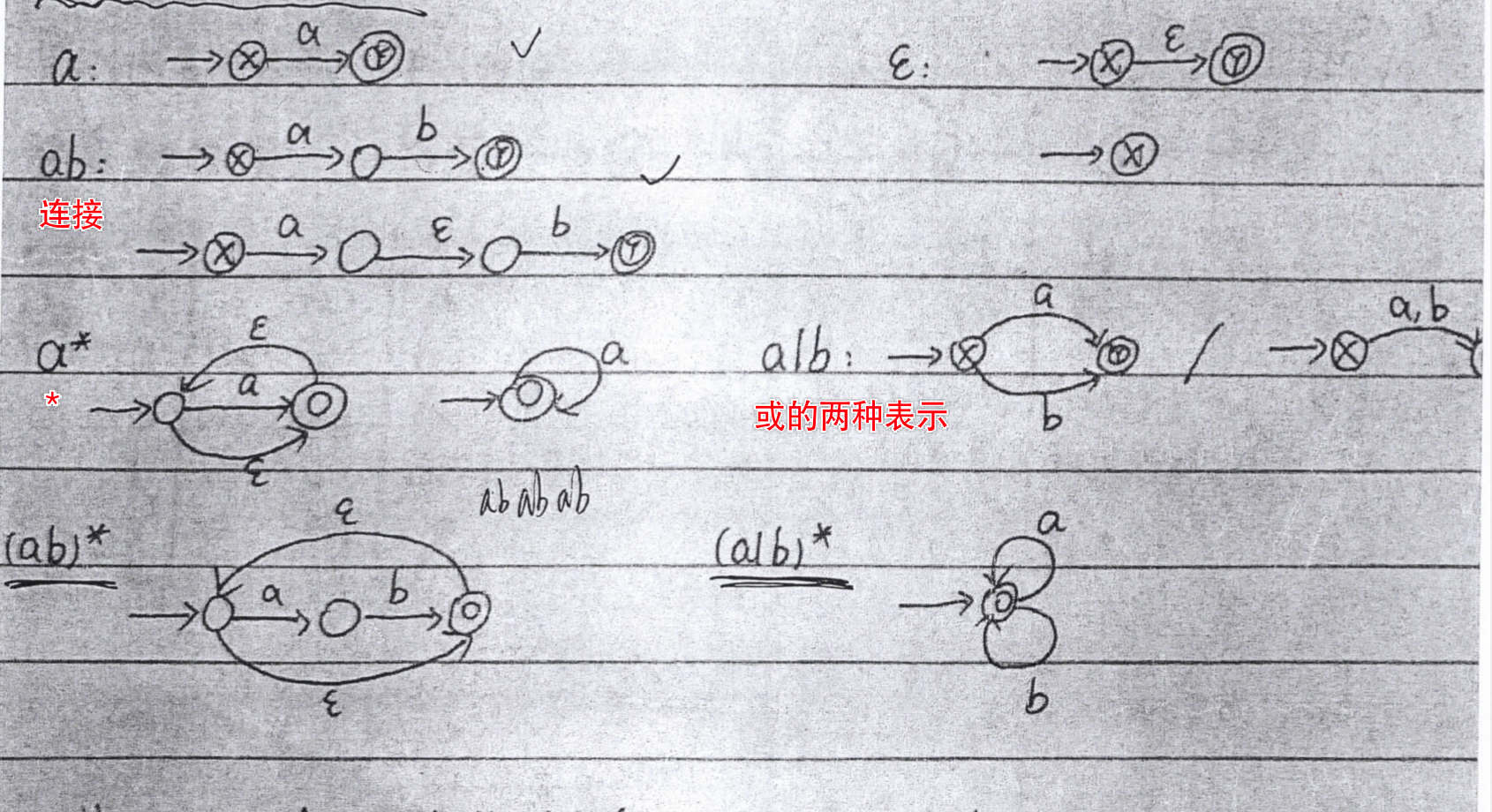
对于$\ast$运算符的特别说明：

转换过程为：

1. 将所有的接受/中止状态使用 $\epsilon$ 箭头 , 从 接受/终止状态 指向 开始状态 ;
2. 添加新的开始状态： 添加接受状态作为开始状态 , 指向开始状态 ;

图例：

二、DFA(Deterministic Finite Automaton)

有穷自动机。如果一个语言可以被有穷自动机识别则称之为正则语言，其定义为一个五元组

定义：

$DFA=(Q,\Sigma ,q_0,F,\delta )$

说明：

1. $Q$ : 有穷集合，状态集
2. $\Sigma$ ：有穷集合，字母集
3. $q_0$ : $q_0\in Q$, 表示开始/起始状态 (start/initial state)
4. $F$ : $F\subseteq Q$ , 表示最终/接受状态 (final/accept state)
5. $\delta$ : $Q_1\times \Sigma \to Q_2$ 转移函数

理解： 类比于状态转移图

Q： 图中所有的节点

$\Sigma$：边的集合

$q_0$：初始节点

$F$：最终节点（双圈）

$\epsilon$ : 图中的逻辑规则

图例：

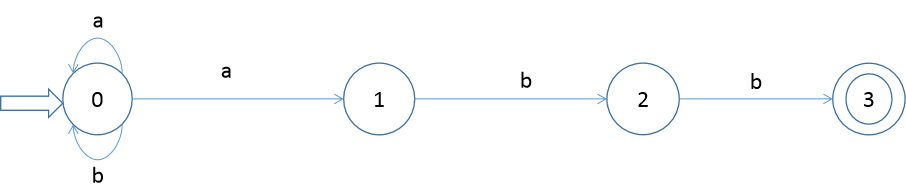
$s\in S,a\in \Sigma ,\delta (s,a)$表示从状态s出发，沿着标记a所能到达的状态

例：当$s=0,a=a$时，从状态0出发，经过a只能够到达1

三、NFA(Non-deterministic Finite Automaton)

非确型有穷自动机。同样是五元组

定义：

$NFA=(Q,\Sigma ,q_0,F,\delta )$

说明：

1. 前四个与DFA定义相同
2. $\delta$ : $Q_1\times \Sigma \to P(Q)$ $P(Q)$表示一个状态的子集

图例：

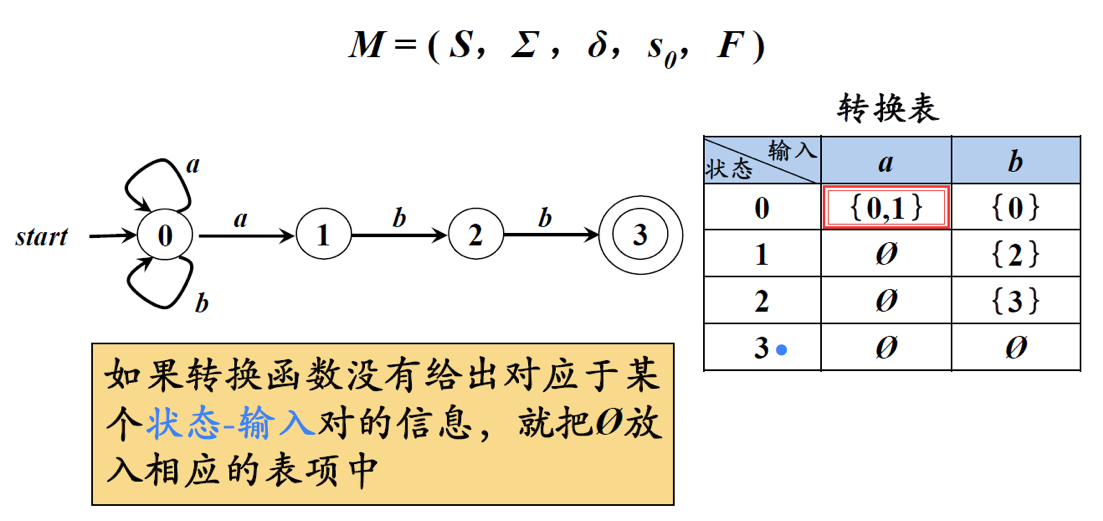
$s\in S,a\in \Sigma ,\delta (s,a)$表示从状态s出发，沿着标记a所能到达的状态集合

因为可能是一个状态集合，所以NFA的状态图可能有不同的后继

例：当$s=0,a=a$时，能够到达的状态集合是 { 0 , 1 } \{0, 1\} { 0,1}

---

NFA与DFA的不同：

1. $\epsilon -transation$ is allowed 允许读入一个空串即$\epsilon$ (状态转移结果还是自身)
2. Many possible next states at each step 每一步都可能有多种可能性

NFA可以使用**(subset construct)子集构造法**转换为DFA

练习1：

1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} )，其中 f(0,a)={0,1} f(0,b)={0} f(1,b)={2} f(2,b)={3}

画出状态转换矩阵,状态转换图，并说明该NFA识别的是什么样的语言。

NFA	a	b
0	0,1	0
1	$\varnothing$	2
2	$\varnothing$	3
3	$\varnothing$	$\varnothing$

语言：$(a|b)\ast abb$

四、子集构造法：NFA转化为DFA

在有穷自动机的理论里，有这样的定理：设L为一个由不确定的有穷自动机接受的集合，则存在一个接受L的确定的有穷自动机

所以非确定有穷自动机NFA可以转换为DFA，对于上面的例1流程如下：

第一步 构建自定义状态$I$

子集构造法，简单来说思路就是将一些状态作为集合成为一个新的状态

$I$的初始选择规则：从初始状态$q_0$经过任意数量的$\epsilon$能够到达的状态的集合

对于例1来说，上例就是状态0

$I_x$表示集合$I$的每个状态节点经过$x$（可经过$\epsilon$）的所有结果集合的并集

对于上例来说，只有一个0状态节点，所以，状态0经过a可以到达的状态集合是{0,1}, 经过b可以到达的状态集合是{0}

下面选择$I$的规则是： 从上一次的所有$I_x，x\in \Sigma$中选择一个作为$I$，但是每个$I_x$只可选择一次

对于上例来说，可以只能选择{0, 1}，因为{0}已经在最开始选择了（为了避免自定义的重复），作为$I$, 则其对应的$I_a、I_b$如下图

0的 I a = { 0 ， 1 } , I b = { 0 } I_a = \{0， 1\}, I_b = \{0\} Ia​={ 0，1},Ib​={ 0} , 1的 I a = ∅ , I b = { 2 } I_a = \varnothing, I_b = \{2\} Ia​=∅,Ib​={ 2} => (取并集) I a = { 0 , 1 } , I b = { 0 , 2 } I_a = \{0, 1\}, I_b = \{0, 2\} Ia​={ 0,1},Ib​={ 0,2}

同理选择下一个 I = { 0 , 2 } I = \{0, 2\} I={ 0,2}, 继续计算….

	$I$	$I_a$	$I_b$
A	{0}	{0, 1}	{0}
B	{0, 1}	{0, 1}	{0, 2}
C	{0, 2}	{0, 1}	{0, 3}
D	{0, 3}	{0, 1}	{0}

最终自定义状态为：A={0}, B={0, 1}, C={0, 2}, D={0, 3}

第二步 画出DFA状态转移图

首先根据上面的表格就立即可以得出状态转移表：

DFA	a	b
A	B	A
B	B	C
C	B	D
D	B	A

画出状态转移图像：

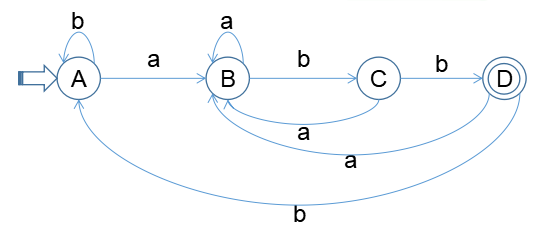
检查图中没有同一输入的多后继节点则说明满足DFA

例2

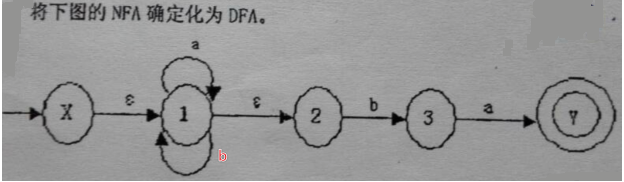
答案：

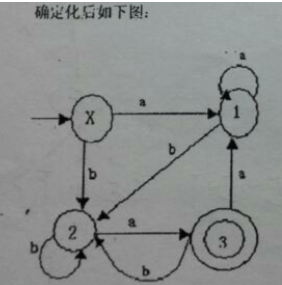
五、Pumping lemma 泵定理

正则语言都需要满足泵定理，泵引理是形式语言与自动机理论中判定一个语言不是正则语言的重要工具

定义

For every regular language L, there is a pumping length $P$, such that for any string $S\in L$ and $|S|\ge P$, We can divide $S$ into 3 pieces and write $S=xyz$ with:

1.$x{y}^{i}z\in L$ For every i ∈ { 0 , 1 , 2 , 3 , … } i\in \{0,1,2,3,…\} i∈{ 0,1,2,3,…}

2.$|y|\ge 1$
3.$|xy|\le P$

Note that 1 implies that $xz\in L$

2 say that y cannot be the empty string $\epsilon$ (2 说明了y不能是空串)

condition 3 is not always used

中文版：

使用

简单的来说，使用的过程就是不断的Pump（重复）其中的若干部分，使得到新的字符串仍满足RL，所以一般使用反证法去反证

例1:

证明 $0^n{1}^{n}n\ge 0$不是一个RL (regular language)

证明如下：

assume that B = { 0 n 1 n , n ≥ 0 } B = \{0^n1^n,n\ge0\} B={ 0n1n,n≥0} is regular language (反证法： 假设B是一个RL)

let p be the pumping length, and $S=0^p{1}^p\in B$ （设一个pumping 长度为p，则可得到S，其长度刚刚好为p，满足不小于p）

then $S=0^p{1}^p=xyz$ （根据RL满足的泵定理，将S分割为三个部分）

let $x=0^{p-k},y=0^k,z=1^p,k>0$ （分别假设每一个部分xyz的值）

so, $xy=0^p$, it meets the $|xy|=p\le p$ （验证第三个条件，满足）

because k > 0, so, it meets the $|y|\ge 1$ （验证第二个条件，满足）

but, （验证第三个条件，不满足，所以不是一个RL）

$$\begin{gathered} x{y}^{1}z=0^{p-k}{0}^k{1}^p=0^p{1}^p\in B, \\ x{y}^{2}z=0^{p-k}{0}^{2k}{1}^p=0^{p+k}{1}^p\notin B, \\ x{y}^{3}z=0^{p-k}{0}^{3k}{1}^p=0^{p+2k}{1}^p\notin B, \\ ... \end{gathered}$$

The pumping result does not hold,the languge B is not regular

例2

证明 E = { 0 i 1 j   i > j } E=\{0^i1^j \ i>j\} E={ 0i1j i>j}不是RL

证明如下：

Assume that $E$ is a regular language with pumping length p

let $S=xyz=0^{p+1}{1}^p\in E$

let $x=0^{p-k},y=0^k,z=01^p,k>0$

so, it meets the $|xy|=p\le p$ and $|y|\ge 1$

$$\begin{gathered} x{y}^{2}z=0^{p-k}{0}^{2k}01^p=0^{p+k+1}{1}^p\in E \\ x{y}^{3}z=0^{p-k}{0}^{3k}01^p=0^{p+2k+1}{1}^p\in E \\ ... \end{gathered}$$

so, if $i\ge 0$, it meets $x{y}^{i}z\in E$,

but, if $i=0$, $S=xz=0^{p-k+1}{1}^p,k>1\notin E$

so, The pumping result does not hold,the languge E is not regular