在连续空间内的规划
第三章:几何表示与变换
构建和解决运动规划问题需要在空间中定义复杂的几何模型并对其进行操作,3.1节介绍了几何模型,其关注点在于半代数模型构建,这也是第五章和第六章的基础。3.2节和3.3节分别介绍了如何变换一个机器人和一条机器人链,这也是运动的基础。
3.1 几何模型
几何模型的替代表示方法有很多,主要有两种:1)边界表示(boundary representation) ,例如一个行星的表面;2)实心表示(solid representation),将包含在球面内的所有点均被描述在模型内。
第一步,定义世界(world, W \mathcal{W} W),二维世界的 W = R 2 \mathcal{W}=\mathbb{R}^{2} W=R2和三维世界的 W = R 3 \mathcal{W}=\mathbb{R}^{3} W=R3,亦或是更高维度的空间。世界中通常含有两类实体:障碍物 O \mathcal{O} O和机器人 R \mathcal{R} R,他们都是世界集的子集。接下来就需要定义这两个集合,使他们便于计算。
3.1.1 多边形和多面体模型
本节将使用障碍物 O \mathcal{O} O的一种实心表示:即一系列基集合(primitive) H i H_i Hi的组合,每个基集合都便于表示和计算。这里可以表示成m个半平面的交。
凸多边形(Convex Polygons):首先考虑障碍物范围是2D世界的一个凸多边形子集, W = R 2 \mathcal{W}=\mathbb{R}^{2} W=R2。一个子集 X ⊂ R n X \subset \mathbb{R}^{n} X⊂Rn被称为凸集当且仅当: ∀ x 1 , x 2 ∈ X , λ ∈ [ 0 , 1 ] , λ x 1 + ( 1 − λ ) x 2 ∈ X \forall x_{1}, x_{2} \in X, \lambda \in[0,1] ,\lambda x_{1}+(1-\lambda) x_{2} \in X ∀x1,x2∈X,λ∈[0,1],λx1+(1−λ)x2∈X。不满足此的称为非凸。
半平面的表示:首先一条通过 ( x 1 , y 1 ) \left(x_{1}, y_{1}\right) (x1,y1)和 ( x 2 , y 2 ) \left(x_{2}, y_{2}\right) (x2,y2)的直线方程可以写成 a x + b y + c = 0 a x+b y+c=0 ax+by+c=0,其中参数都是由两个点确定的。令 f : R 2 → R f: \mathbb{R}^{2} \rightarrow \mathbb{R} f:R2→R, f ( x , y ) = a x + b y + c . f(x, y)=a x+b y+c . f(x,y)=ax+by+c.那么,令 f ( x , y ) < 0 f(x, y)<0 f(x,y)<0代表了直线的左侧。令 f i ( x , y ) f_{i}(x, y) fi(x,y)表示凸边形的第i条边从 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi)到 ( x i + 1 , y i + 1 ) , 1 ≤ i < m , \left(x_{i+1}, y_{i+1}\right), 1 \leq i<m, (xi+1,yi+1),1≤i<m, 令 f m ( x , y ) f_{m}(x, y) fm(x,y)表示 ( x m , y m ) \left(x_{m}, y_{m}\right) (xm,ym) to ( x 1 , y 1 ) \left(x_{1}, y_{1}\right) (x1,y1)。因此半平面可以表示为 W \mathcal{W} W的一个子集:
H i = { ( x , y ) ∈ W ∣ f i ( x , y ) ≤ 0 } H_{i}=\left\{(x, y) \in \mathcal{W} \mid f_{i}(x, y) \leq 0\right\} Hi={
(x,y)∈W∣fi(x,y)≤0}一个m条边的凸多边形障碍区域可以表示为式(3.3):
O = H 1 ∩ H 2 ∩ ⋯ ∩ H m \mathcal{O}=H_{1} \cap H_{2} \cap \cdots \cap H_{m} O=H1∩H2∩⋯∩Hm
凹多边形(Nonconvex Polygons):若 O \mathcal{O} O是一个非凸多边形,可以表示为式(3.4)
O = O 1 ∪ O 2 ∪ ⋯ ∪ O n \mathcal{O}=\mathcal{O}_{1} \cup \mathcal{O}_{2} \cup \cdots \cup \mathcal{O}_{n} O=O1∪O2∪⋯∪On其中 O i \mathcal{O_i} Oi是凸多边形,彼此之间可以相交。而表示非凸多边形的方式不唯一。一种高效的方法是将 O \mathcal{O} O进行正交分解,会在第6章讲到。
定义逻辑符(Defining a logical predicate):我们可以将定义逻辑符视为一个碰撞检测器。令 ϕ : W → { \phi: \mathcal{W} \rightarrow\{ ϕ:W→{
TRUE, FALSE } \} },若返回true,则该世界中的点位于障碍物范围内。对于一条线 f ( x , y ) = 0 f(x, y)=0 f(x,y)=0,令 e ( x , y ) = 0 e(x, y)=0 e(x,y)=0代表一个逻辑判断,如果返回TRUE,则代表 f ( x , y ) ≤ 0 f(x, y)\leq 0 f(x,y)≤0.
关于凸多边形区域的逻辑判断可以表示为式(3.5):
α ( x , y ) = e 1 ( x , y ) ∧ e 2 ( x , y ) ∧ ⋯ ∧ e m ( x , y ) \alpha(x, y)=e_{1}(x, y) \wedge e_{2}(x, y) \wedge \cdots \wedge e_{m}(x, y) α(x,y)=e1(x,y)∧e2(x,y)∧⋯∧em(x,y)式中 ∧ \wedge ∧表示逻辑与,当上式返回TRUE,则表示点 ( x , y ) (x,y) (x,y)在凸多边形内。
一个包含n个凸多边形的障碍物区域可以表示为式(3.6):
ϕ ( x , y ) = α 1 ( x , y ) ∨ α 2 ( x , y ) ∨ ⋯ ∨ α n ( x , y ) \phi(x, y)=\alpha_{1}(x, y) \vee \alpha_{2}(x, y) \vee \cdots \vee \alpha_{n}(x, y) ϕ(x,y)=α1(x,y)∨α2(x,y)∨⋯∨αn(x,y)即使有更加快速有效的方法,但是式(3.6)可以检验点 ( x , y ) (x,y) (x,y)是否在 O ( n ) O(n) O(n)时刻在 O \mathcal{O} O内。
多面体模型(Polyhedral models):多面体模型可以由点、线和面组成,每个面都是平整的,双连通边列表作为一种数据结构包含了三种元素:面、半边(有向边)和点。每个顶点记录保存点坐标和指向与顶点接触的任意半边的指针。每个面记录包含指向其边界上任意半边的指针。多边形的每一条边都由一对半边记录。每一条半边包含了5个指向其他元素的指针:1)半边的起始点;2)另一半的半边(相邻面的边界,方向相反);3)以该边为边界的面;4)在循环边列表里面的下一条半边;5)在循环边列表里面的上一条半边
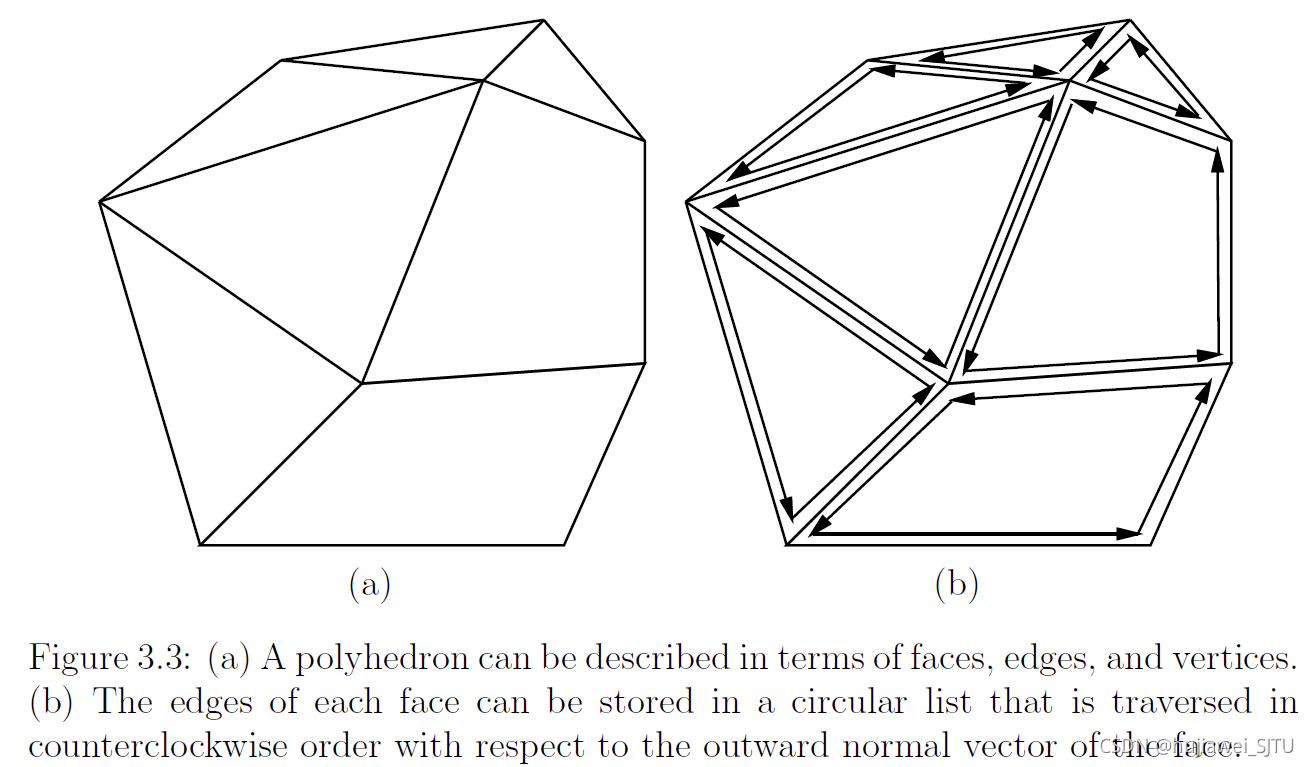
现在考虑多边形的实心表示(solid representation),假设 O \mathcal{O} O是一个凸多边形,如图3.3所示。每一个面至少由三个点构成,假设三个点不共线,则任意一个通过该直线的面可以表示为式(3.7):
a x + b y + c z + d = 0 , a , b , c , d ∈ R ax+by+cz+d=0,a,b,c,d \in \mathbb{R} ax+by+cz+d=0,a,b,c,d∈R令 f : R 3 → R f: \mathbb{R}^{3} \rightarrow \mathbb{R} f:R3→R,则如式(3.8)
f ( x , y , z ) = a x + b y + c z + d . f(x,y,z)=ax+by+cz+d. f(x,y,z)=ax+by+cz+d.对于有 m m m个面的凸多面体,每个半平面 H i H_{i} Hi都是世界 W \mathcal{W} W的子集
H i = { ( x , y , z ) ∈ W ∣ f i ( x , y , z ) ≤ 0 } H_{i}=\left\{(x, y, z) \in \mathcal{W} \mid f_{i}(x, y, z) \leq 0\right\} Hi={
(x,y,z)∈W∣fi(x,y,z)≤0}凸多面体可以视为是一系列半平面的交集,非凸多面体可以视为是一系列半平面的并集。 ϕ ( x , y , z ) \phi(x, y, z) ϕ(x,y,z)可以用类似的方式定义,当返回TRUE时 ( x , y , z ) ∈ O (x, y, z) \in \mathcal{O} (x,y,z)∈O.
3.1.2 半代数模型
在多边形和多面体模型中, f f f是一个多项式。在2D环境中, f f f是关于 x , y x,y x,y的多项式;在3D环境中, f f f是关于 x , y , z x,y,z x,y,z的多项式。半代数模型包含多边形和多面体模型,其中 f f f是一次多项式。由单个多项式元确定的点集称为代数集。由有限个代数集的并集和交集得到的点集称为半代数集。
考虑2D世界,一个实心表示可以通过代数单元集(algebraic primitives)表示:
H = { ( x , y ) ∈ W ∣ f ( x , y ) ≤ 0 } H=\{(x, y) \in \mathcal{W} \mid f(x, y) \leq 0\} H={
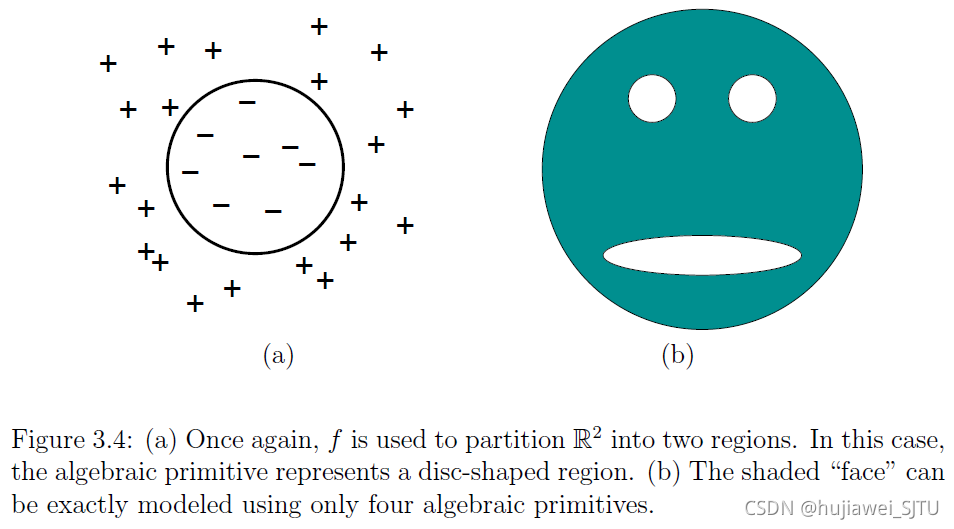
(x,y)∈W∣f(x,y)≤0}其中若 f = x 2 + y 2 − 4 f=x^{2}+y^{2}-4 f=x2+y2−4,则表示了一个圆盘,如图3.4(a)所示。
笑脸集(图3.4 (b)):
f 1 = x 2 + y 2 − r 1 2 f 2 = − ( ( x − x 2 ) 2 + ( y − y 2 ) 2 − r 2 2 ) f 3 = − ( ( x − x 3 ) 2 + ( y − y 3 ) 2 − r 3 2 ) f 4 = − ( x 2 / a 2 + ( y − y 4 ) 2 / b 2 − 1 ) \begin{aligned} &f_{1}=x^{2}+y^{2}-r_{1}^{2} \\ &f_{2}=-\left(\left(x-x_{2}\right)^{2}+\left(y-y_{2}\right)^{2}-r_{2}^{2}\right) \\ &f_{3}=-\left(\left(x-x_{3}\right)^{2}+\left(y-y_{3}\right)^{2}-r_{3}^{2}\right) \\ &f_{4}=-\left(x^{2} / a^{2}+\left(y-y_{4}\right)^{2} / b^{2}-1\right) \end{aligned} f1=x2+y2−r12f2=−((x−x2)2+(y−y2)2−r22)f3=−((x−x3)2+(y−y3)2−r32)f4=−(x2/a2+(y−y4)2/b2−1) O = H 1 ∩ H 2 ∩ H 3 ∩ H 4 \mathcal{O}=H_{1} \cap H_{2} \cap H_{3} \cap H_{4} O=H1∩H2∩H3∩H4可以发现,一系列障碍物区域的交集不一定是凸集,因此逻辑运算符 ϕ ( x , y ) \phi(x,y) ϕ(x,y)将继续起到作用。
在三维空间内,半代数方式表示的结果为(3.13):
H = { ( x , y , z ) ∈ W ∣ f ( x , y , z ) ≤ 0 } H=\{(x, y, z) \in \mathcal{W} \mid f(x, y, z) \leq 0\} H={
(x,y,z)∈W∣f(x,y,z)≤0}
3.1.3 其他模型
模型类别的选择通常要依据规划算法所采取的操作。
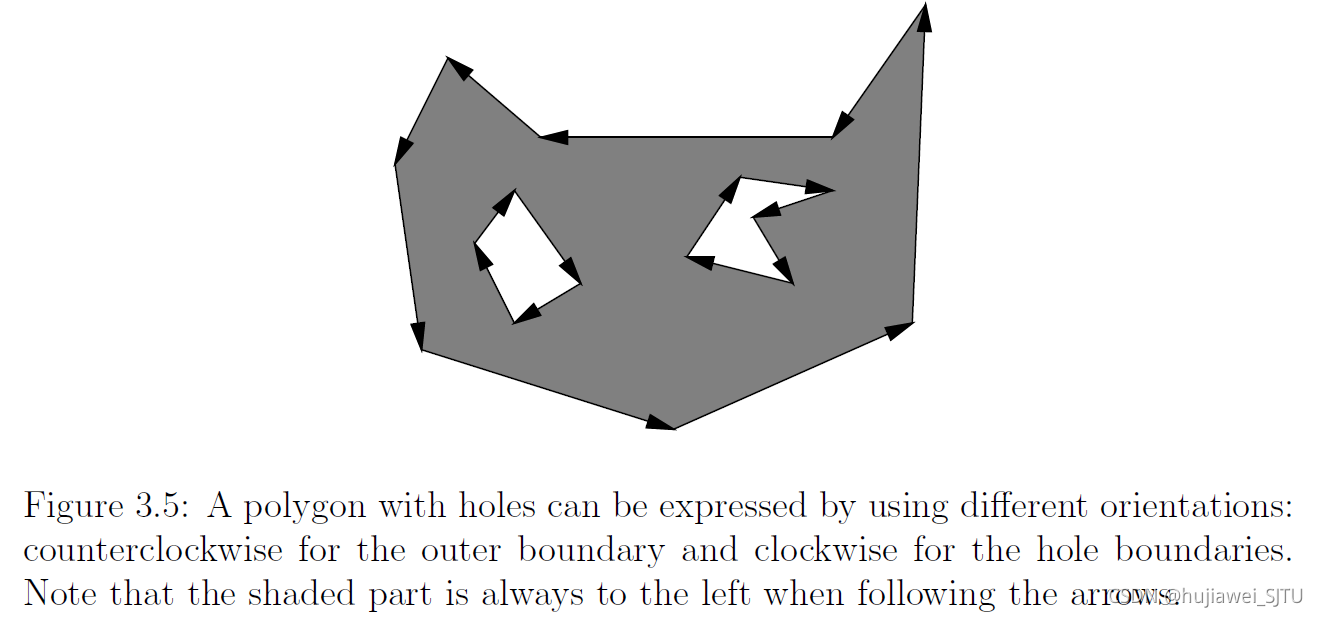
非凸多边形和多面体(Nonconvex polygons and polyhedra): 3.1.1节采用图多边形的并集来表示非凸多边形。与此不同的是,使用边界表示方法来描述非凸多边形时,通过具有特殊排列顺序的点列表示。如图3.5所示,保证多边形在边的左侧。对于3d空间而言,则需要制定面、边、点的序列,而洞需要使用相反的方向重新建模。
3D三角形:令 W = R 3 \mathcal{W}=\mathbb{R}^3 W=R3,最简便的几何模型表示方法是一个三角形集合,每个三角形可以表示为一组点集 ( x 1 , y 1 , z 1 ) , ( x 2 , y 2 , z 2 ) , ( x 3 , y 3 , z 3 ) (x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3) (x1,y1,z1),(x2,y2,z2),(x3,y3,z3),如图3.6所示。没有可利用的一致性来简单地声明一个点是在 3D 障碍物的“内部”还是“外部” 。那么有时最好减少三角形坐标规范中的冗余(许多三角形将共享相同的角)。 采用了三角带(triangle strip),即是一系列三角形,且每对邻居有一个共同边。或者三角扇(triangle fan),即每个三角形共用一个点。
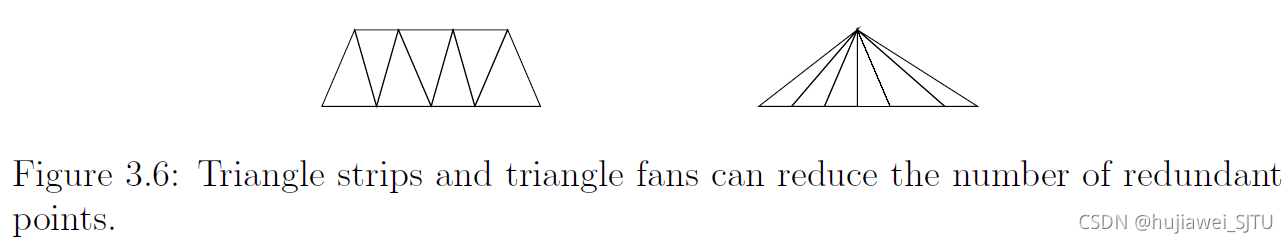
非均匀有理 B 样条(Nonuniform rational B-splines, NURBS):这些被用于许多工程设计系统,以便在飞机或汽车车身设计等应用中方便地设计和调整曲面。 与作为隐式方程的半代数模型相比,NURBS 和其他样条是参数方程。 这使得渲染等计算更容易; 然而,其他的,如碰撞检测,变得更加困难。 这些模型可以在任何维度上定义。 这里给出了一个简短的 2D 公式。
C ( u ) = ∑ i = 0 n w i P i N i , k ( u ) ∑ i = 0 n w i N i , k ( u ) C(u)=\frac{\sum_{i=0}^{n} w_{i} P_{i} N_{i, k}(u)}{\sum_{i=0}^{n} w_{i} N_{i, k}(u)} C(u)=∑i=0nwiNi,k(u)∑i=0nwiPiNi,k(u)其中 w i ∈ R w_i \in \mathbb{R} wi∈R是权重, P i P_{i} Pi是控制点, N i , k N_{i, k} Ni,k是 k 阶的归一化基函数(normalized basis functions of degree k),可以通过递归地(recursively)表示:
N i , k ( u ) = ( u − t i t i + k − t i ) N i , k − 1 ( u ) + ( t i + k + 1 − u t i + k + 1 − t i + 1 ) N i + 1 , k − 1 ( u ) N_{i, k}(u)=\left(\frac{u-t_{i}}{t_{i+k}-t_{i}}\right) N_{i, k-1}(u)+\left(\frac{t_{i+k+1}-u}{t_{i+k+1}-t_{i+1}}\right) N_{i+1, k-1}(u) Ni,k(u)=(ti+k−tiu−ti)Ni,k−1(u)+(ti+k+1−ti+1ti+k+1−u)Ni+1,k−1(u)递归的起点是
N i , 0 ( u ) = 1 if t i ≤ u < t i + 1 , and N i , 0 ( u ) = 0 otherwise N_{i, 0}(u)=1 \text { if } t_{i} \leq u<t_{i+1}, \text { and } N_{i, 0}(u)=0 \text { otherwise } Ni,0(u)=1 if ti≤u<ti+1, and Ni,0(u)=0 otherwise 结向量(knot vector)是实数值的非递减序列 { t 0 , t 1 , . . . , t m } \left \{t_0, t_1,...,t_m \right \} {
t0,t1,...,tm},控制某些基本功能生效的时间间隔。
位图(Bitmaps):典型的位图是灰度图(gray-scale map 或占用网格(occupancy grid)。
超二次曲面 (Superquadrics):除了使用多项式定义 f i f_i fi,还可以使用很多其他的函数类型。比如用超二次曲面来构建二次曲面。例如超椭球体:对 W = R 3 \mathcal{W} =\mathbb{R}^3 W=R3
( ∣ x / a ∣ n 1 + ∣ y / b ∣ n 2 ) n 1 / n 2 + ∣ z / c ∣ n 1 − 1 ≤ 0 \left(|x / a|^{n_{1}}+|y / b|^{n_{2}}\right)^{n_{1} / n_{2}}+|z / c|^{n_{1}}-1 \leq 0 (∣x/a∣n1+∣y/b∣n2)n1/n2+∣z/c∣n1−1≤0 n 1 ≥ 2 , n 2 ≥ 2 n_1 \geq 2, n_2 \geq 2 n1≥2,n2≥2, 如果 n 1 = n 2 = 2 n_1=n_2=2 n1=n2=2,则产生椭圆。随着 n 1 , n 2 n_1,n_2 n1,n2增加,超椭球变成一个圆角的盒子(b站小电视)。
广义圆柱体(Generalized cylinders):广义圆柱体的中心轴线是一条曲线 ( x ( s ) , y ( s ) , z ( s ) ) , s ∈ [ 0 , 1 ] (x(s), y(s), z(s)),s \in [0,1] (x(s),y(s),z(s)),s∈[0,1],而圆柱的半径也是一个沿着轴变化的变量 r ( s ) r(s) r(s).
3.2 刚体变换
3.2.1 基本概念
令 O \mathcal{O} O代表障碍物区域,令 A \mathcal{A} A代表机器人区域,它是“移动”的 ,可能是 R 2 \mathbb{R^2} R2或者 R 3 \mathbb{R^3} R3,这与 W \mathcal{W} W一致。刚体变换是函数 h : A → W h:\mathcal{A} \to\mathcal{W} h:A→W,同时必须保证1) A \mathcal{A} A中的点与点之间的距离不变;2) A \mathcal{A} A的方向保留(不出现镜像)。 h ( a ) h(a) h(a)表示映射到 W \mathcal{W} W中的点,
h ( A ) = { h ( a ) ∈ W ∣ a ∈ A } h(\mathcal{A})=\{h(a) \in \mathcal{W} \mid a \in \mathcal{A}\} h(A)={
h(a)∈W∣a∈A}这是 h h h 的映射,表示变换后的机器人在 W \mathcal{W} W中占据的所有点。
机器人模型变换:若 A \mathcal{A} A表示 R 2 \mathbb{R^2} R2内的指定点,若采用边界表示方法,则很容易的采用h函数映射到世界中。若采用实心表示中的半平面集合模型,则需要先定义 w ∈ W w \in \mathcal{W} w∈W,作为 h ( a ) ∈ W h(a) \in \mathcal{W} h(a)∈W的逆函数, a = h − 1 ( w ) a=h^{-1}(w) a=h−1(w).
h ( H i ) = { w ∈ W ∣ f i ( h − 1 ( w ) ) ≤ 0 } h\left(H_{i}\right)=\left\{w \in \mathcal{W} \mid f_{i}\left(h^{-1}(w)\right) \leq 0\right\} h(Hi)={
w∈W∣fi(h−1(w))≤0}
一个参数化的变换族 (A parameterized family of transformation):定义参数向量 q ∈ R n q \in \mathbb{R}^n q∈Rn,变换后的点为 h ( q , a ) h(q,a) h(q,a),机器人集合变换后为 h ( q , A ) ⊂ W h(q,\mathcal{A}) \subset \mathcal{W} h(q,A)⊂W. h ( q , a ) h(q,a) h(q,a)采用简记形式 a ( q ) a(q) a(q), h ( q , A ) h(q,\mathcal{A}) h(q,A)采用简记形式 A ( q ) \mathcal{A}(q) A(q)。这个符号表明,通过调整参数 q q q,机器人 A \mathcal{A} A在 W \mathcal{W} W中四处移动,因为从预定的族中选择了不同的变换。 A ( q ) \mathcal{A}(q) A(q)可以被考虑为一个设定值函数,当 A \mathcal{A} A被 q q q 变换时,产生 W \mathcal{W} W中被 A \mathcal{A} A占据的点集。
定义框架(Defining frames): A \mathcal{A} A(body frame)和 W \mathcal{W} W (world frame)属于不同的坐标系,变换可以视为是一种坐标变换。
3.2.2 二维变换
平移:刚体机器人 A ⊂ R 2 \mathcal{A} \subset \mathbb{R}^2 A⊂R2的平移使用了 q = ( x t , y t ) , x t , y t ∈ R q=(x_t,y_t),x_t,y_t \in \mathbb{R} q=(xt,yt),xt,yt∈R. 边界表示法表示的 A \mathcal{A} A可以用下式依序移动多边形的边界点实现
h ( x , y ) = ( x + x t , y + y t ) h(x,y)=(x+x_t,y+y_t) h(x,y)=(x+xt,y+yt)对于实心表示法表示的 A \mathcal{A} A,定义一些列的元集(primitives):
H i = { ( x , y ) ∈ W ∣ f ( x , y ) ≤ 0 } H_{i}=\left\{(x, y) \in \mathcal{W} \mid f(x, y) \leq 0\right\} Hi={
(x,y)∈W∣f(x,y)≤0}变换为 h ( H i ) = { ( x , y ) ∈ W ∣ f ( x − x t , y − y t ) ≤ 0 } . h\left(H_{i}\right)=\left\{(x, y) \in \mathcal{W} \mid f\left(x-x_{t}, y-y_{t}\right) \leq 0\right\} . h(Hi)={
(x,y)∈W∣f(x−xt,y−yt)≤0}.变换的两种方式:1)世界坐标系固定,移动机器人;2)机器人固定,移动坐标系。本书采用第一种方式。
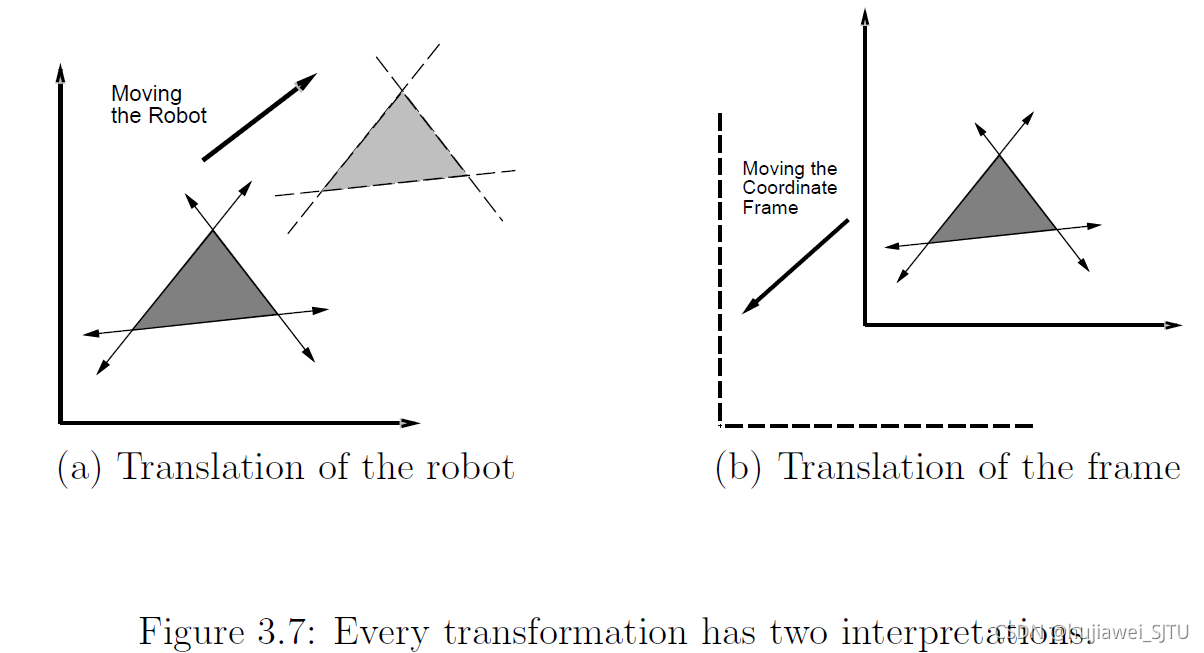
旋转: ( x , y ) ∈ A (x,y) \in \mathcal{A} (x,y)∈A通过逆时针旋转 θ ∈ [ 0 , 2 π ] \theta \in [0,2\pi] θ∈[0,2π].
( x , y ) ↦ ( x cos θ − y sin θ , x sin θ + y cos θ ) (x, y) \mapsto(x \cos \theta-y \sin \theta, x \sin \theta+y \cos \theta) (x,y)↦(xcosθ−ysinθ,xsinθ+ycosθ)其中2x2的旋转矩阵R如下所示
R ( θ ) = ( cos θ − sin θ sin θ cos θ ) R(\theta)=\left(\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right) R(θ)=(cosθsinθ−sinθcosθ)因此旋转可以表示为矩阵形式
( x cos θ − y sin θ x sin θ + y cos θ ) = R ( θ ) ( x y ) \left(\begin{array}{l} x \cos \theta-y \sin \theta \\ x \sin \theta+y \cos \theta \end{array}\right)=R(\theta)\left(\begin{array}{l} x \\ y \end{array}\right) (xcosθ−ysinθxsinθ+ycosθ)=R(θ)(xy)使用3.2.1里的概念, R ( θ ) R(\theta) R(θ)就是 h ( q ) h(q) h(q), q = θ q=\theta q=θ.
平移和旋转
( cos θ − sin θ x t sin θ cos θ y t 0 0 1 ) ( x y 1 ) = ( x cos θ − y sin θ + x t x sin θ + y cos θ + y t 1 ) \left(\begin{array}{ccc} \cos \theta & -\sin \theta & x_{t} \\ \sin \theta & \cos \theta & y_{t} \\ 0 & 0 & 1 \end{array}\right)\left(\begin{array}{l} x \\ y \\ 1 \end{array}\right)=\left(\begin{array}{c} x \cos \theta-y \sin \theta+x_{t} \\ x \sin \theta+y \cos \theta+y_{t} \\ 1 \end{array}\right) ⎝⎛cosθsinθ0−sinθcosθ0xtyt1⎠⎞⎝⎛xy1⎠⎞=⎝⎛xcosθ−ysinθ+xtxsinθ+ycosθ+yt1⎠⎞定义3x3的齐次变换矩阵 T T T:
T = ( cos θ − sin θ x t sin θ cos θ y t 0 0 1 ) T=\left(\begin{array}{ccc} \cos \theta & -\sin \theta & x_{t} \\ \sin \theta & \cos \theta & y_{t} \\ 0 & 0 & 1 \end{array}\right) T=⎝⎛cosθsinθ0−sinθcosθ0xtyt1⎠⎞
3.2.3 三维变换
3D平移: ( x , y , z ) ↦ ( x + x t , y + y t , z + z t ) (x, y, z) \mapsto\left(x+x_{t}, y+y_{t}, z+z_{t}\right) (x,y,z)↦(x+xt,y+yt,z+zt),对于 H i = { ( x , y , z ) ∈ W ∣ f i ( x , y , z ) ≤ 0 } H_{i}=\left\{(x, y, z) \in \mathcal{W} \mid f_{i}(x, y, z) \leq 0\right\} Hi={ (x,y,z)∈W∣fi(x,y,z)≤0}变换为 { ( x , y , z ) ∈ W ∣ f i ( x − x t , y − y t , z − z t ) ≤ 0 } \left\{(x, y, z) \in \mathcal{W} \mid f_{i}\left(x-x_{t}, y-y_{t}, z-z_{t}\right) \leq 0\right\} { (x,y,z)∈W∣fi(x−xt,y−yt,z−zt)≤0}
偏航、俯仰和横滚旋转
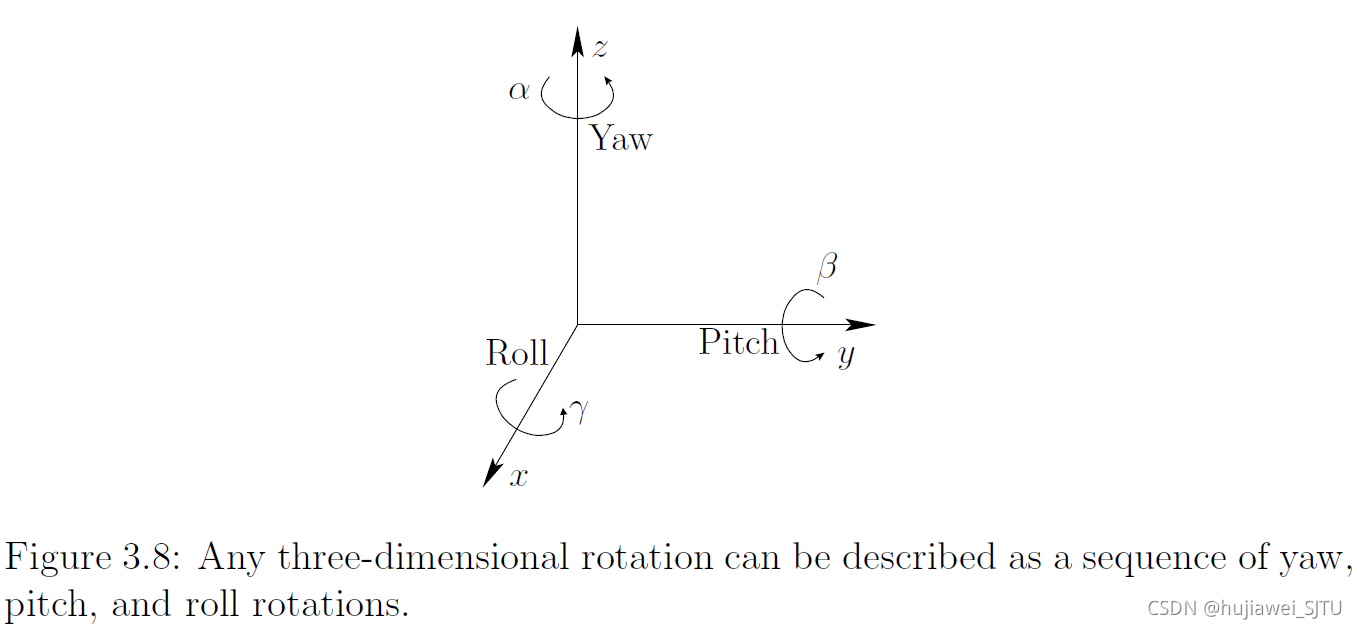
偏航(yaw):z轴旋转: R z ( α ) = ( cos α − sin α 0 sin α cos α 0 0 0 1 ) R_{z}(\alpha)=\left(\begin{array}{ccc} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{array}\right) Rz(α)=⎝⎛cosαsinα0−sinαcosα0001⎠⎞
俯仰(pitch):y轴旋转: R y ( β ) = ( cos β 0 sin β 0 1 0 − sin β 0 cos β ) R_{y}(\beta)=\left(\begin{array}{ccc} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{array}\right) Ry(β)=⎝⎛cosβ0−sinβ010sinβ0cosβ⎠⎞
横滚(roll):x轴旋转: R x ( γ ) = ( 1 0 0 0 cos γ − sin γ 0 sin γ cos γ ) R_{x}(\gamma)=\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \gamma & -\sin \gamma \\ 0 & \sin \gamma & \cos \gamma \end{array}\right) Rx(γ)=⎝⎛1000cosγsinγ0−sinγcosγ⎠⎞得到角度旋转合成的旋转矩阵: R ( α , β , γ ) = R z ( α ) R y ( β ) R x ( γ ) = ( cos α cos β cos α sin β sin γ − sin α cos γ cos α sin β cos γ + sin α sin γ sin α cos β sin α sin β sin γ + cos α cos γ sin α sin β cos γ − cos α sin γ − sin β cos β sin γ cos β cos γ ) . \begin{aligned} &R(\alpha, \beta, \gamma)=R_{z}(\alpha) R_{y}(\beta) R_{x}(\gamma)= \\ &\qquad\left(\begin{array}{ccc} \cos \alpha \cos \beta & \cos \alpha \sin \beta \sin \gamma-\sin \alpha \cos \gamma & \cos \alpha \sin \beta \cos \gamma+\sin \alpha \sin \gamma \\ \sin \alpha \cos \beta & \sin \alpha \sin \beta \sin \gamma+\cos \alpha \cos \gamma & \sin \alpha \sin \beta \cos \gamma-\cos \alpha \sin \gamma \\ -\sin \beta & \cos \beta \sin \gamma & \cos \beta \cos \gamma \end{array}\right) . \end{aligned} R(α,β,γ)=Rz(α)Ry(β)Rx(γ)=⎝⎛cosαcosβsinαcosβ−sinβcosαsinβsinγ−sinαcosγsinαsinβsinγ+cosαcosγcosβsinγcosαsinβcosγ+sinαsinγsinαsinβcosγ−cosαsinγcosβcosγ⎠⎞.
通过旋转矩阵得到rpy角度:对于 ( r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 ) \left(\begin{array}{lll} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{array}\right) ⎝⎛r11r21r31r12r22r32r13r23r33⎠⎞得到 α , β , γ \alpha,\beta,\gamma α,β,γ,其中 tan − 1 \tan ^{-1} tan−1可以用C语言中的atan2替代: α = tan − 1 ( r 21 / r 11 ) β = tan − 1 ( − r 31 / r 32 2 + r 33 2 ) γ = tan − 1 ( r 32 / r 33 ) \begin{gathered} \alpha=\tan ^{-1}\left(r_{21} / r_{11}\right) \\ \beta=\tan ^{-1}\left(-r_{31} / \sqrt{r_{32}^{2}+r_{33}^{2}}\right)\\ \gamma=\tan ^{-1}\left(r_{32} / r_{33}\right) \end{gathered} α=tan−1(r21/r11)β=tan−1(−r31/r322+r332)γ=tan−1(r32/r33)其中 r 11 ≠ 0 , r 33 ≠ 0 r_{11} \neq 0,r_{33} \neq 0 r11=0,r33=0
3D齐次变换矩阵:顺序rpy,平移 T = ( cos α cos β cos α sin β sin γ − sin α cos γ cos α sin β cos γ + sin α sin γ x t sin α cos β sin α sin β sin γ + cos α cos γ sin α sin β cos γ − cos α sin γ y t − sin β cos β sin γ cos β cos γ z t 0 0 0 1 ) . T=\left(\begin{array}{cccc} \cos \alpha \cos \beta & \cos \alpha \sin \beta \sin \gamma-\sin \alpha \cos \gamma & \cos \alpha \sin \beta \cos \gamma+\sin \alpha \sin \gamma & x_{t} \\ \sin \alpha \cos \beta & \sin \alpha \sin \beta \sin \gamma+\cos \alpha \cos \gamma & \sin \alpha \sin \beta \cos \gamma-\cos \alpha \sin \gamma & y_{t} \\ -\sin \beta & \cos \beta \sin \gamma & \cos \beta \cos \gamma & z_{t} \\ 0 & 0 & 0 & 1 \end{array}\right) . T=⎝⎜⎜⎛cosαcosβsinαcosβ−sinβ0cosαsinβsinγ−sinαcosγsinαsinβsinγ+cosαcosγcosβsinγ0cosαsinβcosγ+sinαsinγsinαsinβcosγ−cosαsinγcosβcosγ0xtytzt1⎠⎟⎟⎞.使用3.2.1节概念, A ( x t , y t , z t , α , β , γ ) \mathcal{A}(x_t,y_t,z_t,\alpha,\beta,\gamma) A(xt,yt,zt,α,β,γ)
3.3 物体运动链的变换
对于一组链式链接的刚体机器人,变换变得更加复杂。为了简便处理,将机器人视为连杆(link),令 A 1 , A 2 , . . . , A m \mathcal{A}_1,\mathcal{A}_2,...,\mathcal{A}_m A1,A2,...,Am表示一组连杆,对于 1 ≤ i ≤ m 1 \leq i \leq m 1≤i≤m连杆 A i \mathcal{A}_i Ai与 A i + 1 \mathcal{A}_{i+1} Ai+1以某种方式连接,使得这允许 A i + 1 \mathcal{A}_{i+1} Ai+1 相对于 A i \mathcal{A}_{i} Ai 进行一些受约束的运动。 运动约束必须显示的给出。本节考虑在单个链中连接的刚体,并将这特定链接称为运动链。
3.3.1 二维运动链
假设两个不相交的机器人 A 1 , A 2 ⊂ W \mathcal{A}_1,\mathcal{A}_2 \sub \mathcal{W} A1,A2⊂W,每个拥有3自由度, q = ( x 1 , y 1 , z 1 , x 2 , y 2 , z 2 ) q=(x_1,y_1,z_1,x_2,y_2,z_2) q=(x1,y1,z1,x2,y2,z2)
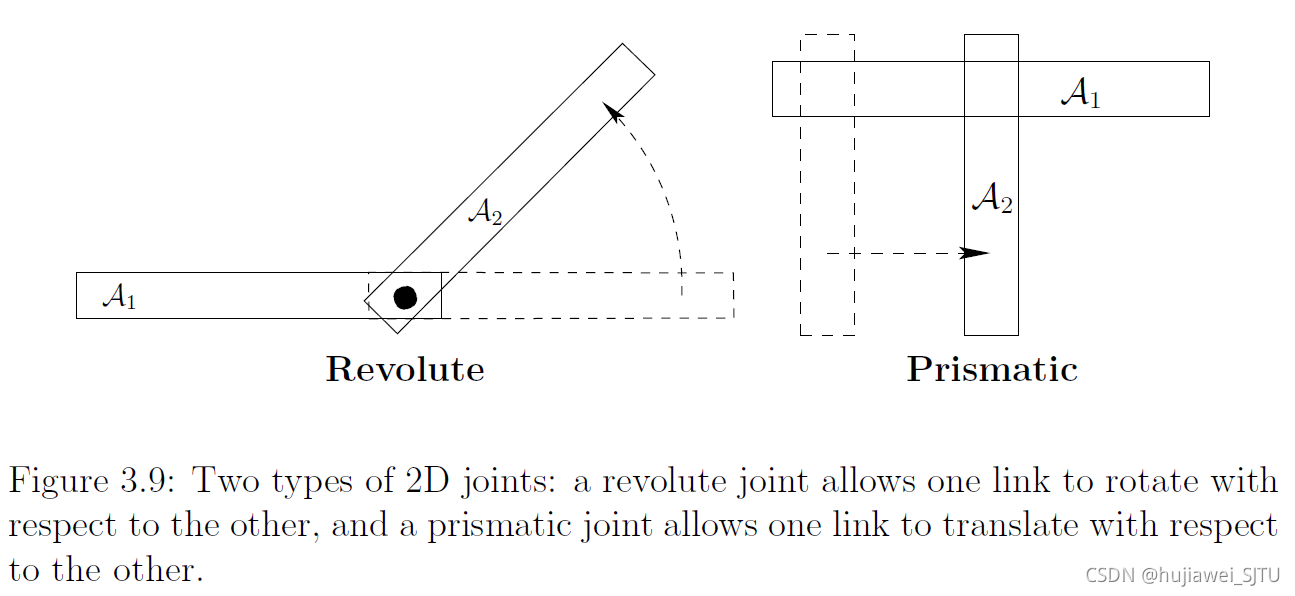
对于运动链,如下图所示, T 1 T 2 ⋯ T m ( x y 1 ) T_{1} T_{2} \cdots T_{m} \left( \begin{array}{l}x \\ y \\ 1\end{array} \right) T1T2⋯Tm⎝⎛xy1⎠⎞
其中 T i = ( cos θ i − sin θ i a i − 1 sin θ i cos θ i 0 0 0 1 ) T_{i}=\left(\begin{array}{ccc} \cos \theta_{i} & -\sin \theta_{i} & a_{i-1} \\ \sin \theta_{i} & \cos \theta_{i} & 0 \\ 0 & 0 & 1 \end{array}\right) Ti=⎝⎛cosθisinθi0−sinθicosθi0ai−101⎠⎞
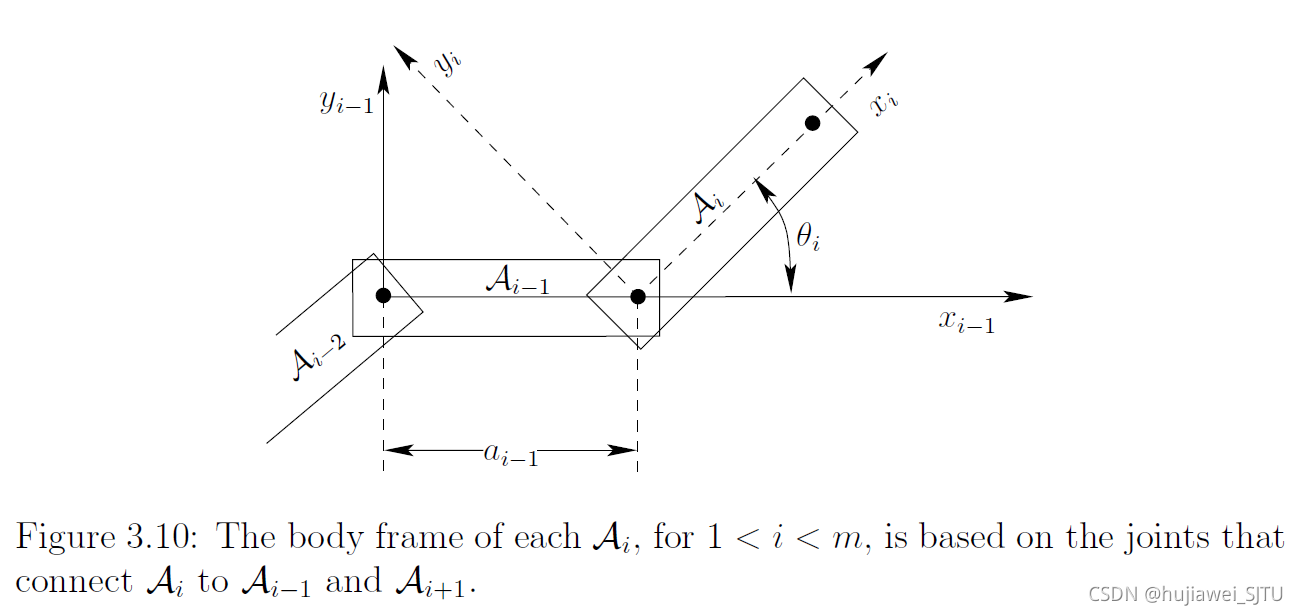
三维运动链:运动副约束如下所示。
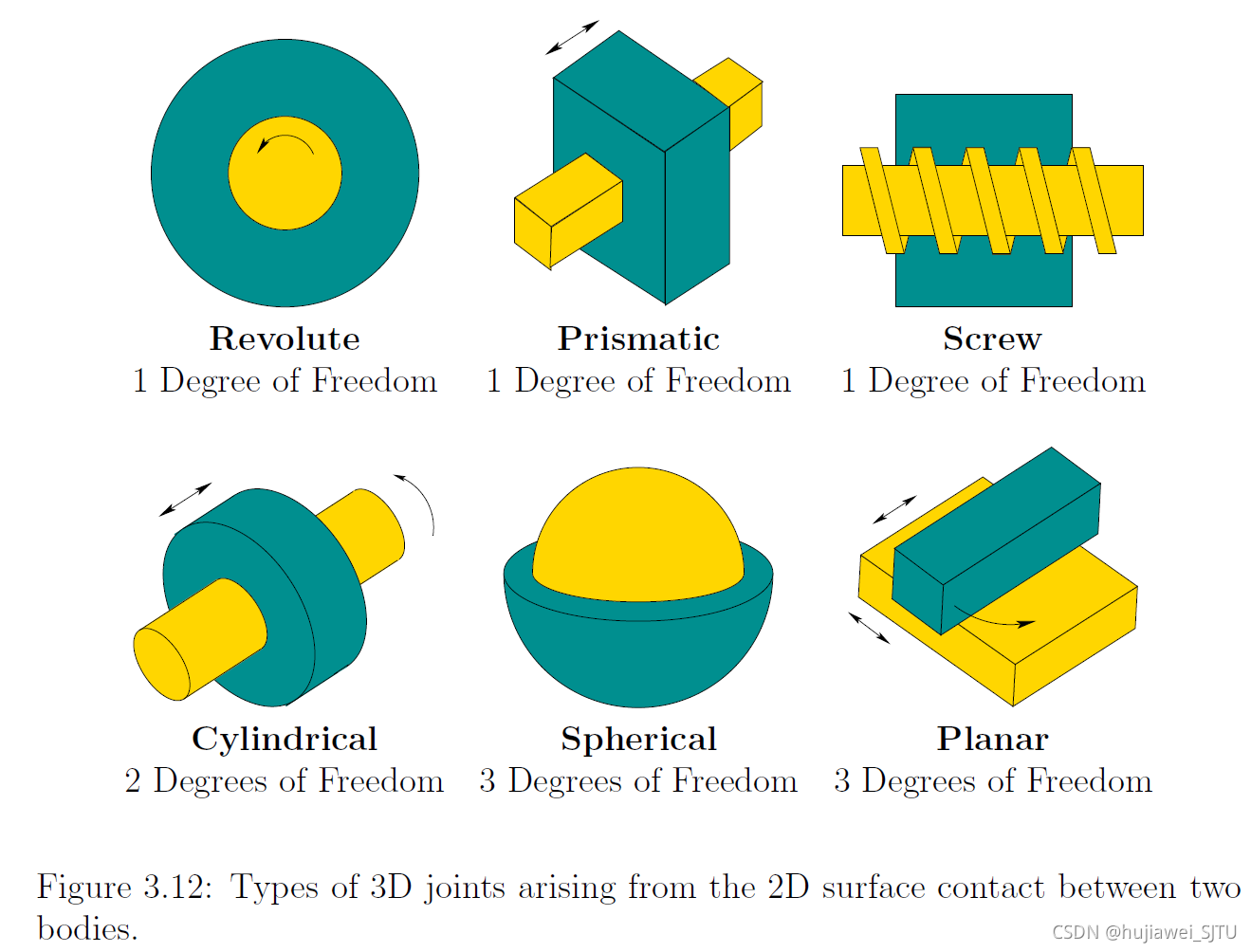
引入DH参数,如下图:
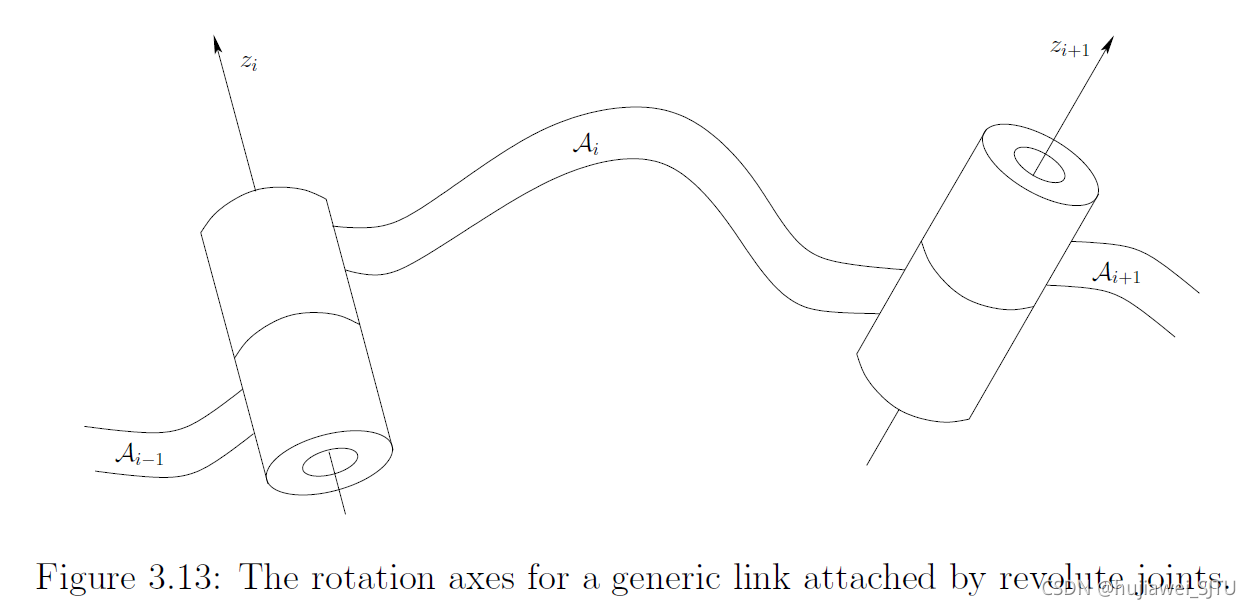
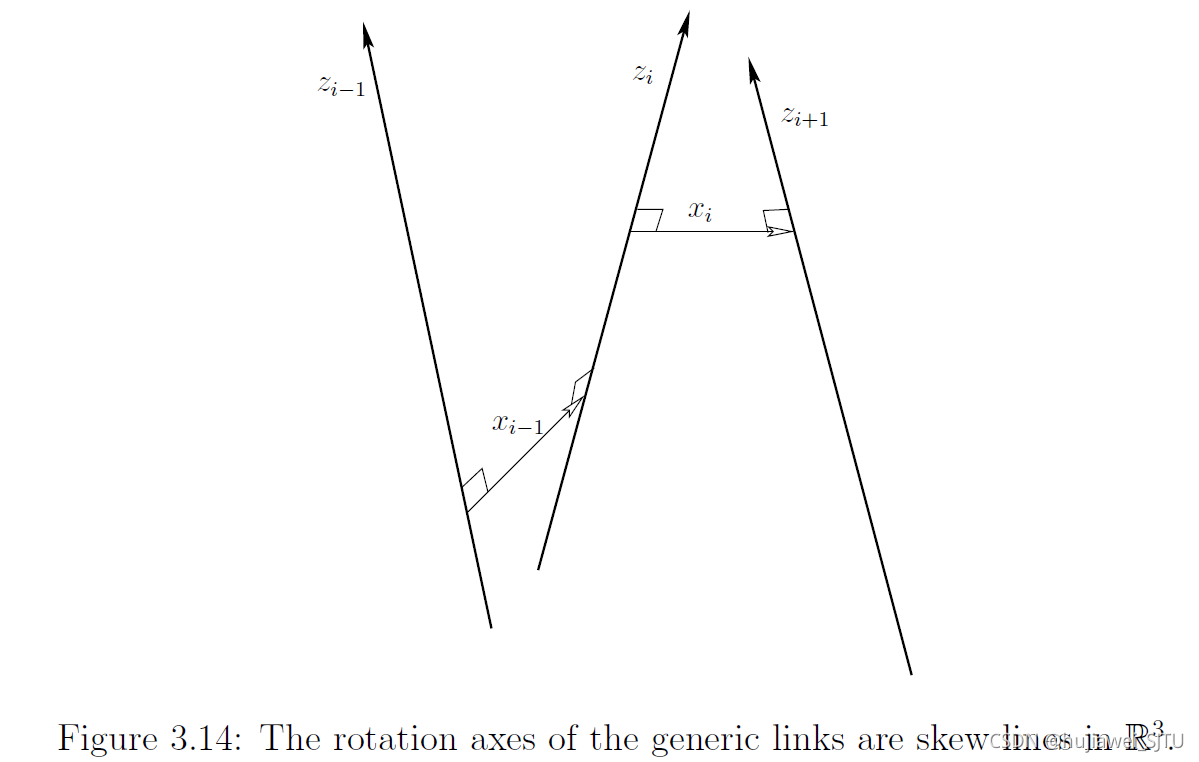
- 沿 z i z_i zi 轴平移 d i d_i di 。
- 绕 z i z_i zi 轴逆时针旋转 θ i \theta_i θi 。
- 沿 x i − 1 x_{i-1} xi−1 轴平移 a i − 1 a_{i-1} ai−1 。
- 绕 x i − 1 x_{i-1} xi−1 轴逆时针旋转 α i − 1 \alpha_{i-1} αi−1 。
R i = ( cos θ i − sin θ i 0 0 sin θ i cos θ i 0 0 0 0 1 d i 0 0 0 1 ) R_{i}=\left(\begin{array}{cccc} \cos \theta_{i} & -\sin \theta_{i} & 0 & 0 \\ \sin \theta_{i} & \cos \theta_{i} & 0 & 0 \\ 0 & 0 & 1 & d_{i} \\ 0 & 0 & 0 & 1 \end{array}\right) Ri=⎝⎜⎜⎛cosθisinθi00−sinθicosθi00001000di1⎠⎟⎟⎞
Q i − 1 = ( 1 0 0 a i − 1 0 cos α i − 1 − sin α i − 1 0 0 sin α i − 1 cos α i − 1 0 0 0 0 1 ) Q_{i-1}=\left(\begin{array}{cccc} 1 & 0 & 0 & a_{i-1} \\ 0 & \cos \alpha_{i-1} & -\sin \alpha_{i-1} & 0 \\ 0 & \sin \alpha_{i-1} & \cos \alpha_{i-1} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) Qi−1=⎝⎜⎜⎛10000cosαi−1sinαi−100−sinαi−1cosαi−10ai−1001⎠⎟⎟⎞
T i = Q i − 1 R i = ( cos θ i − sin θ i 0 a i − 1 sin θ i cos α i − 1 cos θ i cos α i − 1 − sin α i − 1 − sin α i − 1 d i sin θ i sin α i − 1 cos θ i sin α i − 1 cos α i − 1 cos α i − 1 d i 0 0 0 1 ) . T_{i}=Q_{i-1} R_{i}=\left(\begin{array}{cccc}\cos \theta_{i} & -\sin \theta_{i} & 0 & a_{i-1} \\ \sin \theta_{i} \cos \alpha_{i-1} & \cos \theta_{i} \cos \alpha_{i-1} & -\sin \alpha_{i-1} & -\sin \alpha_{i-1} d_{i} \\ \sin \theta_{i} \sin \alpha_{i-1} & \cos \theta_{i} \sin \alpha_{i-1} & \cos \alpha_{i-1} & \cos \alpha_{i-1} d_{i} \\ 0 & 0 & 0 & 1\end{array}\right) . Ti=Qi−1Ri=⎝⎜⎜⎛cosθisinθicosαi−1sinθisinαi−10−sinθicosθicosαi−1cosθisinαi−100−sinαi−1cosαi−10ai−1−sinαi−1dicosαi−1di1⎠⎟⎟⎞.
3.4 运动树变换
在多机器人搬运问题中,每个机器人与物体均有接触,即形成一条运动链,而多机搬运则形成了运动树,
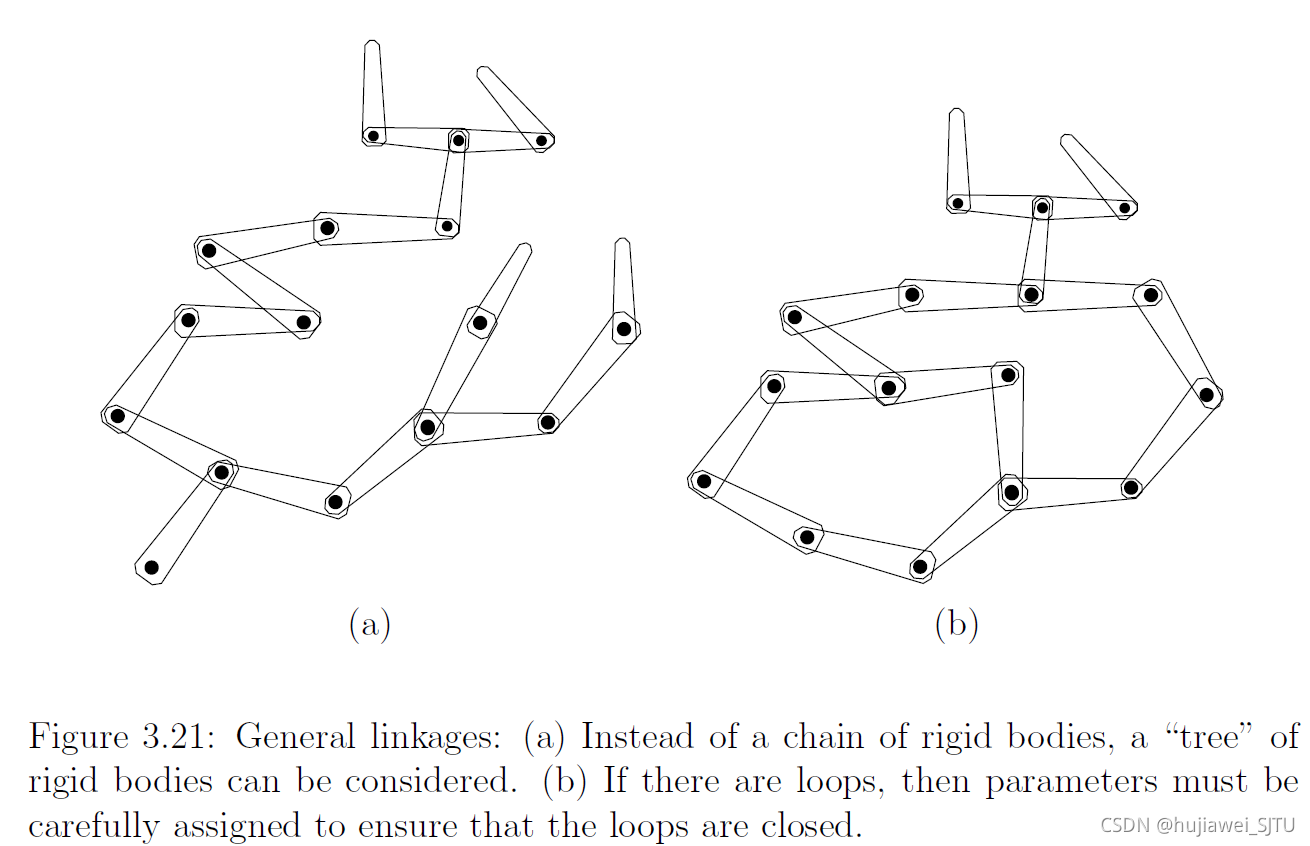
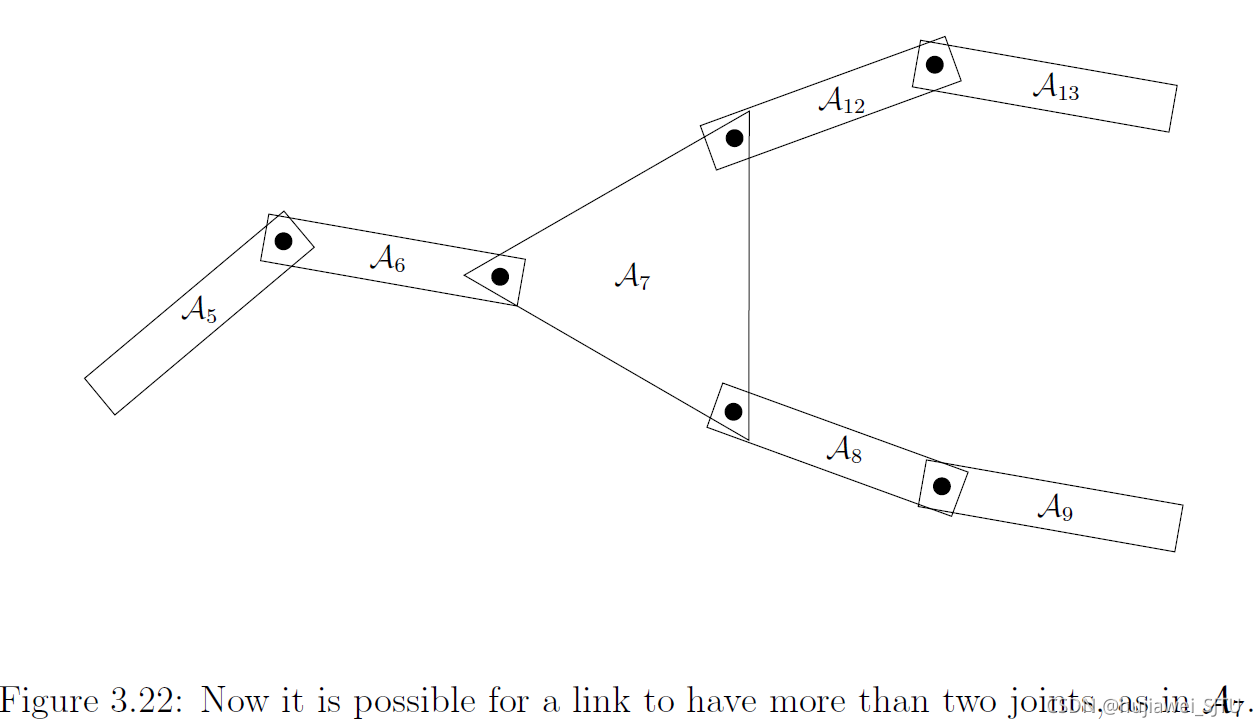
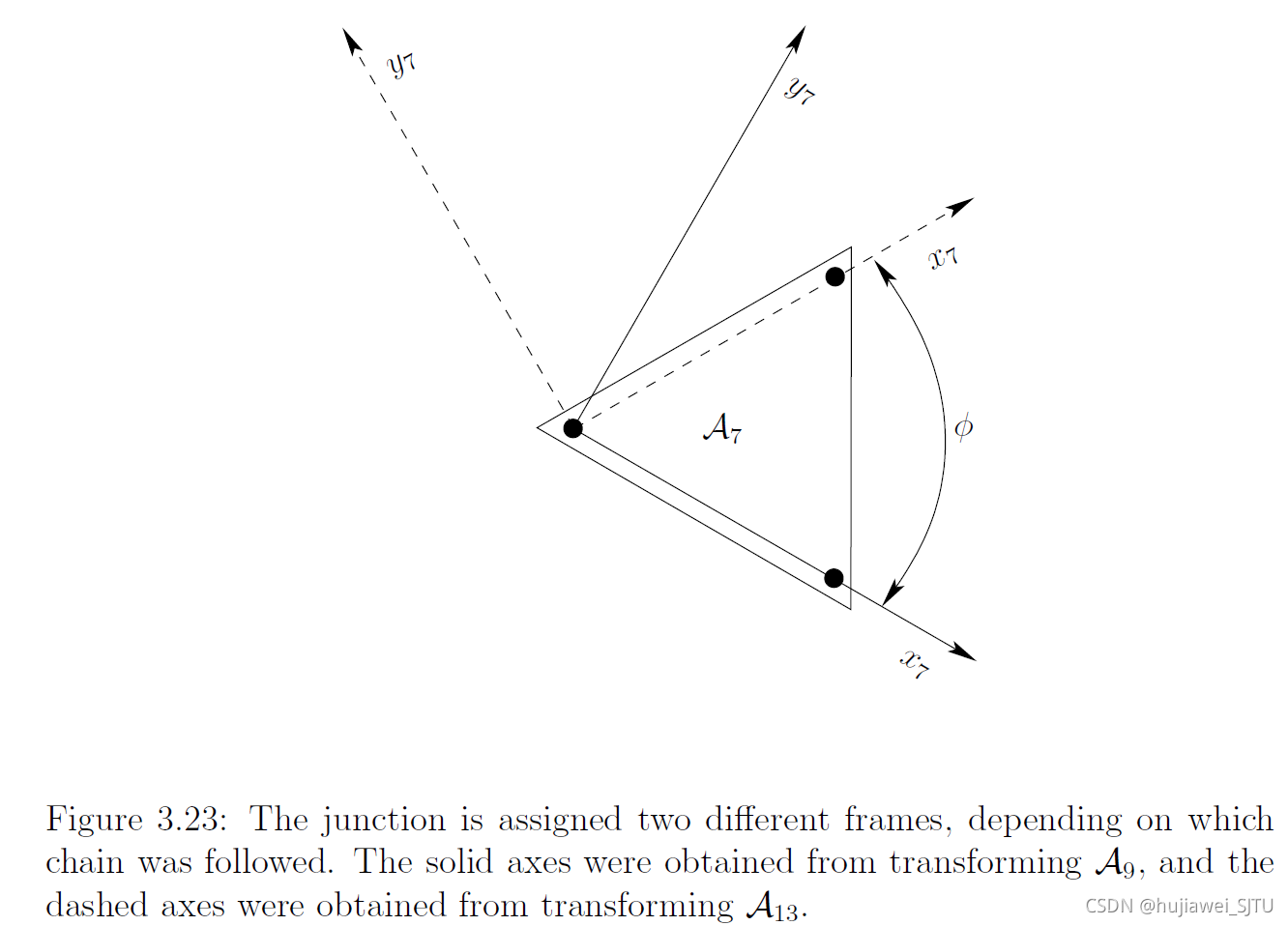
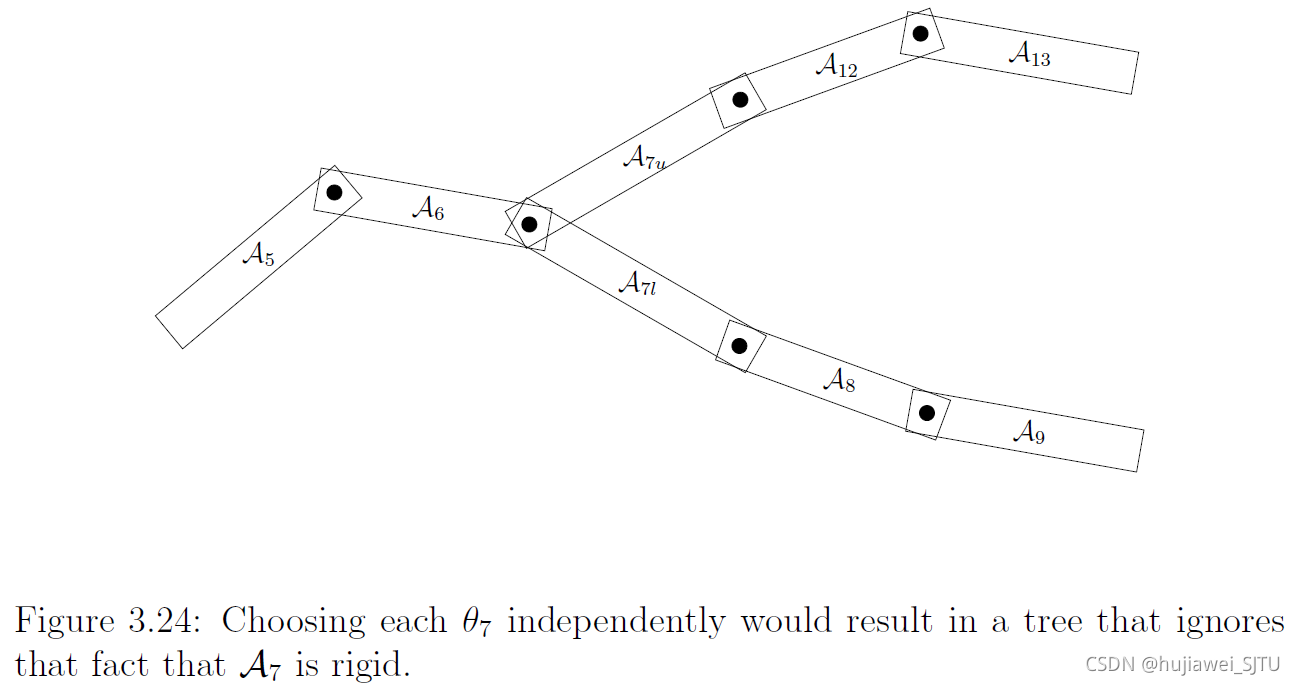
3.5 非刚性变换
以可变形物体为例,需要涉及到非刚性变换。
线性变换:旋转时线性变换的特殊例子,通过矩阵 M n × n M_{n \times n} Mn×n,
机器人的缩放矩阵,通过 m 11 m_{11} m11在x轴上缩放,通过 m 22 m_{22} m22在y轴上缩放,若其中有一个是负数,则会产生镜像。
( m 11 0 0 m 22 ) ( x y ) \left(\begin{array}{cc} m_{11} & 0 \\ 0 & m_{22} \end{array}\right)\left(\begin{array}{l} x \\ y \end{array}\right) (m1100m22)(xy)
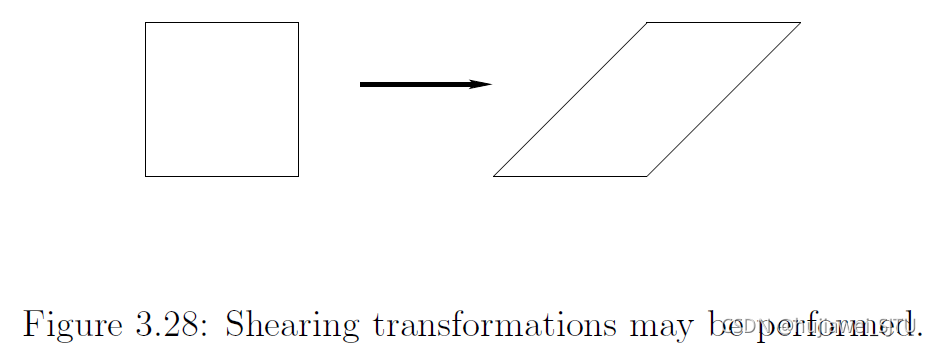
m 12 = 1 m_{12}=1 m12=1如图3.28所示
( 1 m 12 0 1 ) ( x y ) \left(\begin{array}{cc} 1 & m_{12} \\ 0 & 1 \end{array}\right)\left(\begin{array}{l} x \\ y \end{array}\right) (10m121)(xy)
可变形材料:在某些应用中,存在超越线性变换的情况。 想象一下,试图扭曲一种柔性材料使其通过一个走廊,例如床垫。 床垫可以用二维链接阵列来近似; 然而,复杂性和自由度会太麻烦。 再举一个例子,假设一个蛇形机器人是通过将 100 个旋转关节连接在一起而设计的。 3.3 节中的工具可用于将其转换为 100 个旋转参数,1,… . ., 100,但这对于在规划算法中使用可能变得笨拙。 另一种方法是用可变形的曲线或形状来近似蛇。
对于此类问题,最好使用参数化的曲线或曲面族。 样条模型通常是最合适的,因为它们旨在通过调整少量参数来轻松控制曲线的形状。 其他可能性包括第 3.1.3 节中提到的广义圆柱和超二次曲面模型。
一种复杂情况是可能对允许参数的空间施加复杂的约束。 例如,蛇形机器人的每个关节都可以有很小的旋转范围。 这将很容易使用运动链进行建模; 然而,确定样条族中的哪些样条满足这个额外的约束可能很困难。 同样,对于操纵柔性材料,通常存在基于材料弹性的复杂约束。 即使在某些力的作用下确定其正确的形状,也需要整合一个材料上的弹性能量函数。