多维尺度分析MDS详解

一 概述

MDS的初衷是将图结构中的距离在空间的一种表示。例如，已知几个城市的距离，但是不知道城市的坐标，那么MDS就能通过距离矩阵转换成空间坐标向量来近似描述距离。更重要地是，MDS可以更广泛地应用于任意类型的数据实体相似度或距离描述在低维空间的表示。

多维尺度分析MDS的基本思想：用低维空间R^k (k<n)的n个点去重新标度高维空间Rⁿ 的n个实体间的距离或者相似度。将高维空间的n个研究对象简化到低维空间处理，并且保留高维空间中n个对象较高的相似度。

MDS是主要分为两类：度量化多维尺度分析（经典MDS）和非度量化多维尺度分析。经典MDS适用于用距离度量相似度的应用；非度量化MDS适用于无法获得研究对象精确的相似度描述，仅能获得对象之间的等级关系。

MDS于PCA的比较：
相同点：都是数据降维后再进行分析
不同点：PCA选取主成分来降维；MDS通过让标度前后距离尽量相似来构造拟合点

本文详细讨论经典MDS。

二 经典MDS

1. CMDS实现步骤

经典多维尺度分析（CMDS）的思路是：给出n个结点的距离矩阵D，Dij表示节点i与j之间的距离。我们希望将n个节点映射为n个k维向量（平面表示的话k就是2），记作X1,X2,…,Xn，使得Dij≈||Xi-Xj||,即高维空间节点距离用于低维空间向量的距离近似表示。具体算法如下：

• 输入D
• D的所有元素取原值的平方,得距离平方矩阵$\Delta$
• 构造单位矩阵E和n维全1矩阵U
• 计算点积矩阵S = -1/2·(E-U/n)·$\Delta$·(E-U/n)
• 对S进行特征分解S = QΣ² Q^T
• 选取前K个最大的特征值的根号值Σk和正交特征向量Qk
• 降维表示：Dk=${\Sigma }_k{Q}_k^T$

至于上述过程为什么是这样，需要用到数学证明，请看下节。

2. 数学推导

假定在原始空间的n个样本的距离矩阵D$\in$$R^{n\times n}$,其i行j列元素$d_{ij}$表示原始空间中第i个节点和第j个节点间的距离。在低维空间表示矩阵X$\in$$R^{n\times k}$，且使得$||x_i-x_j||=d_{ij}$。令点积矩阵$S=X{X}^T$,$S_{ij}$表示向量$x_i$与$x_j$的内积即$S_{ij}=x_i^T\ast x_j$。此时有如下公式成立：
$$\begin{array}{rl}{d}_{ij}^2& =||x_i-x_j|{|}^2\\ & =(x_i-x_j{)}^2\\ & =||x_i|{|}^2+||x_j|{|}^2-2x_i^T{x}_j\\ & =S_{ii}+S_{jj}-2S_{ij}\end{array}\text{\hspace{1em}(1)}$$

为了数据分析地简便，我们一般希望降维后的数据X均值中心化，即X的各列（或各行)之和为0。此时点积矩阵S各行各列元素之和均为0，即$\sum _{i=1}^n{S}_{ij}=0=\sum _{j=1}^n{S}_{ij}$。点积S矩阵此性质很重要，它可以推到出如下公式：
$$\begin{array}{rl}\sum _{i=1}^n{d}_{ij}^2& =\sum _{i=1}^n(S_{ii}+S_{jj}-2S_{ij})=tr(S)+n{S}_{jj}\text{(}一列距离平方和)\\ \sum _{j=1}^n{d}_{ij}^2& =\sum _{j=1}^n(S_{ii}+S_{jj}-2S_{ij})=tr(S)+n{S}_{ii}\text{(}一行距离平方和)\\ \sum _{i=1}^n\sum _{j=1}^n{d}_{ij}^2& =\sum _{i=1}^n(tr(S)+n{S}_{ii})=2ntr(S)(所有距离平方和)\end{array}$$
推导出上述三个公式用什么用？我们的目的是求S，根据公式（1）可得：$S_{ij}=-\frac{1}{2}(d_{ij}^2-S_{ii}-S_{jj})$。继续看下述推导：
$$\begin{array}{rl}{S}_{ii}& =\frac{1}{n}(\sum _{j=1}^n{d}_{ij}^2-tr(S))\\ S_{jj}& =\frac{1}{n}(\sum _{i=1}^n{d}_{ij}^2-tr(S))\\ -S_{ii}-S_{jj}& =-\frac{1}{n}\sum _{j=1}^n{d}_{ij}^2-\frac{1}{n}\sum _{i=1}^n{d}_{ij}^2+\frac{2}{n}tr(S)\\ & =-\frac{1}{n}\sum _{j=1}^n{d}_{ij}^2-\frac{1}{n}\sum _{i=1}^n{d}_{ij}^2+\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{d}_{ij}^2\end{array}$$
综上所述，可得：
$$\begin{array}{rl}{S}_{ij}& =-\frac{1}{2}(d_{ij}^2-\frac{1}{n}\sum _{j=1}^n{d}_{ij}^2-\frac{1}{n}\sum _{i=1}^n{d}_{ij}^2+\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{d}_{ij}^2)\\ & =-\frac{1}{2}(d_{ij}^2-d_{i.}^2-d_{.j}^2+d_{..}^2)\end{array}$$
即：$S=-\frac{1}{2}(E-\frac{1}{n}U)\Delta (E-\frac{1}{n}U)$。E是单位矩阵，U是全1矩阵，$\Delta$是距离平方矩阵。

最后对S进行特征分解：$S=Q{\Sigma }^2{Q}^T$,选取前k个较大的特征值的根号值和特征向量用于数据降维，即$X={\Sigma }_k{Q}_k^T$。到此实现了，n维空间的n个距离用k（k<<n）维空间的n个坐标来近似描述，这就是经典MDS的核心。

3. 代码实现及案例

#经典MDS
def cmds(D,k):
    m,n =D.shape
    #距离平方矩阵
    delta = D * D
    #全1矩阵
    U = np.zeros((n,n))
    E = np.eye(n)
    #计算内积矩阵
    S = -1.0 / 2 *((E - 1.0/n * U) @ delta @ (E - 1.0/n * U))
    #对内积矩阵进行特征分解
    lambdas,V=np.linalg.eigh(S)
    #翻转特征向量，因为其是按特征值升序排列的
    V = np.flip(V,axis=1)
    Sigma = np.zeros((k,k))
    for i in range(1,k+1):
        Sigma[i-1,i-1] = math.sqrt(lambdas[-i])
    return  Sigma @ V[:,:k].T

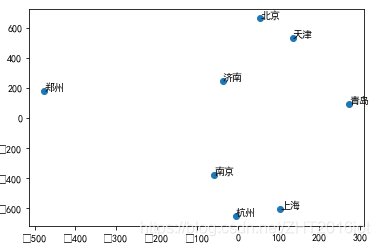
现给出一个案例：我国8大城市的距离如下。

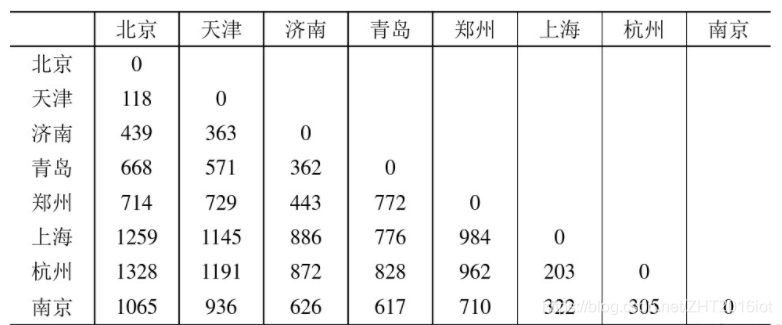
利用上述代码去拟合这个案例的相对位置在平面展示：

D=np.array([0,118,439,668,714,1259,1328,1065,
            118,0,363,571,729,1145,1191,936,
            439,363,0,362,443,886,872,626,
            668,571,362,0,772,776,828,617,
            714,729,443,772,0,984,962,710,
            1259,1145,886,776,984,0,203,322,
            1328,1191,872,828,962,203,0,305,
            1065,936,626,617,710,322,305,0])
labls=['北京','天津','济南','青岛','郑州','上海','杭州','南京']
D=D.reshape(8,8)
Dk=cmds(D,2) * -1
x=Dk[1]
y=Dk[0]
plt.rcParams['font.sans-serif']=['SimHei']
plt.scatter(x, y)
for i in range(len(x)):
    plt.annotate(labls[i], xy = (x[i], y[i]), xytext = (x[i]+0.1, y[i]+0.1))
plt.show()

拟合后的城市相对位置如下图：

总结： MDS是经典的降维算法，其核心思想是利用低维空间的向量距离近似替代高维空间的向量距离，从而保留样本之间差异（距离近似）的同时又进行了降维。