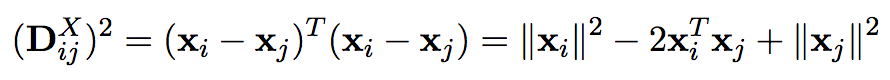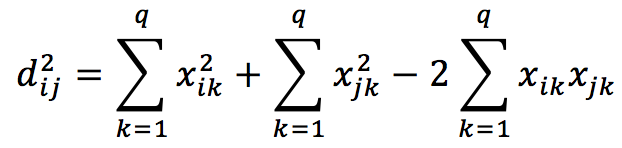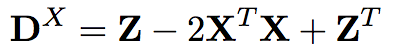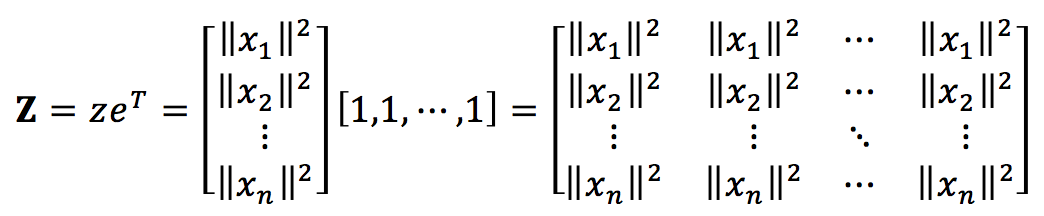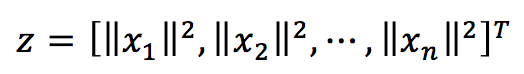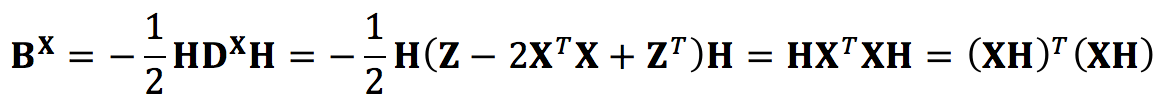详解多维标度法（MDS，Multidimensional scaling）

流形学习（Manifold Learning）是机器学习中一大类算法的统称，而MDS就是其中非常经典的一种方法。多维标度法（Multidimensional Scaling）是一种在低维空间展示“距离”数据结构的多元数据分析技术，简称MDS。

多维标度法解决的问题是：当n个对象（object）中各对对象之间的相似性（或距离）给定时，确定这些对象在低维空间中的表示，并使其尽可能与原先的相似性（或距离）“大体匹配”，使得由降维所引起的任何变形达到最小。多维空间中排列的每一个点代表一个对象，因此点间的距离与对象间的相似性高度相关。也就是说，两个相似的对象由多维空间中两个距离相近的点表示，而两个不相似的对象则由多维空间两个距离较远的点表示。多维空间通常为二维或三维的欧氏空间，但也可以是非欧氏三维以上空间。

多维标度法内容丰富、方法较多。按相似性（距离）数据测量尺度的不同MDS可分为：度量MDS和非度量MDS。当利用原始相似性（距离）的实际数值为间隔尺度和比率尺度时称为度量MDS（metric MDS），本文将以最常用的Classic MDS为例来演示MDS的技术与应用。

首先我们提出这样一个问题，下表是美国十个城市之间的飞行距离，我们如何在平面坐标上据此标出这 10 城市之间的相对位置，使之尽可能接近表中的距离数据呢？

首先我们在R中把csv格式存储的数据文件读入，如下所示：

> data.csv = read.csv("/Users/fzuo/Desktop/data.csv", header = T, row.names = 1)
> data.csv
     ATL  ORD  DEN  HOU  LAX  MIA  JFK  SFO  SEA  IAD
ATL    0  587 1212  701 1936  604  748 2139 2182  543
ORD  587    0  920  940 1745 1188  713 1858 1737  597
DEN 1212  920    0  879  831 1726 1631  949 1021 1494
HOU  701  940  879    0 1374  968 1420 1645 1891 1220
LAX 1936 1745  831 1374    0 2339 2451  347  959 2300
MIA  604 1188 1726  968 2339    0 1092 2594 2734  923
JFK  748  713 1631 1420 2451 1092    0 2571 2408  205
SFO 2139 1858  949 1645  347 2594 2571    0  678 2442
SEA 2182 1737 1021 1891  959 2734 2408  678    0 2329
IAD  543  597 1494 1220 2300  923  205 2442 2329    0

在解释具体原理之前，我们先来调用R中的内置函数来实现上述数据的MDS，并展示一下效果，此处需要用到的函数是cmdscale()。

> citys<-cmdscale(data.csv, k=2)

然后用图形化的方式来展示一下得到的数据点分布图

> cities.names = rownames(data.csv)
> plot(citys[,1],citys[,2],type='n')
> text(citys[,1],citys[,2],cities.names,cex=.7)

执行上述代码，结果如下图所示：

与实际的地图对照，东西方向反了，应该是左东右西，所以可以把上面的绘图代码稍加修改，则有

> plot(-citys[,1],citys[,2],type='n', ylim=c(-600,600)) 
> text(-citys[,1],citys[,2],cities.names,cex=.7)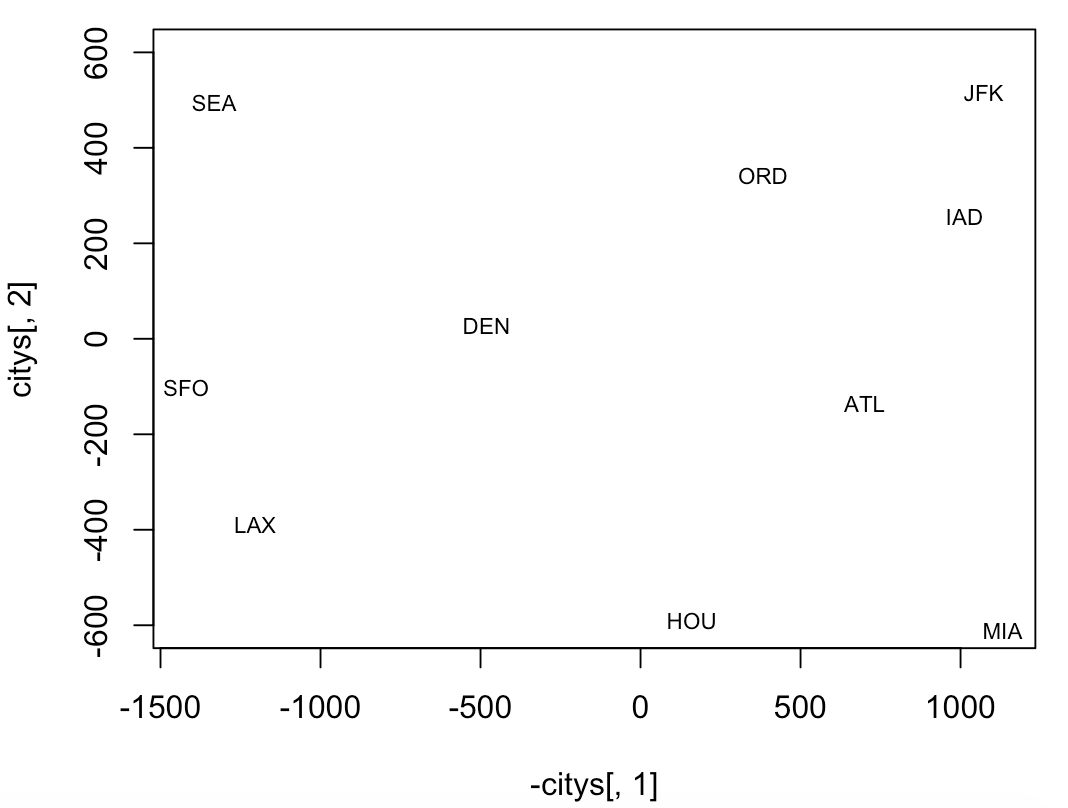

执行上述代码，结果如下图所示：

还可以把上图同实际的美国地图做个对照，易见各个城市在图中的位置与实际情况匹配得相当好。

如此神奇的MDS，它背后的原理到底是什么呢，或者它到底是如何实现的呢？下面我们就来抽丝剥茧。

假设X={x₁, x₂, ..., x_n}是一个n×q的矩阵，n为样本数，q是原始的维度，其中每个x_i是矩阵X的一列，x_i∈R^q。我们并不知道x_i在空间中的具体位置，也就是说对于每个x_i，其坐标(x_i1, x_i2, ... , x_iq) 都是未知的。我们所知道的仅仅是the pair-wise Euclidean distances for X，我们用一个矩阵D^X来表示。因此，对于D^X中的每一个元素，可以写成

或者可以写成

对于矩阵D^X，则有

其中，

这里的z为

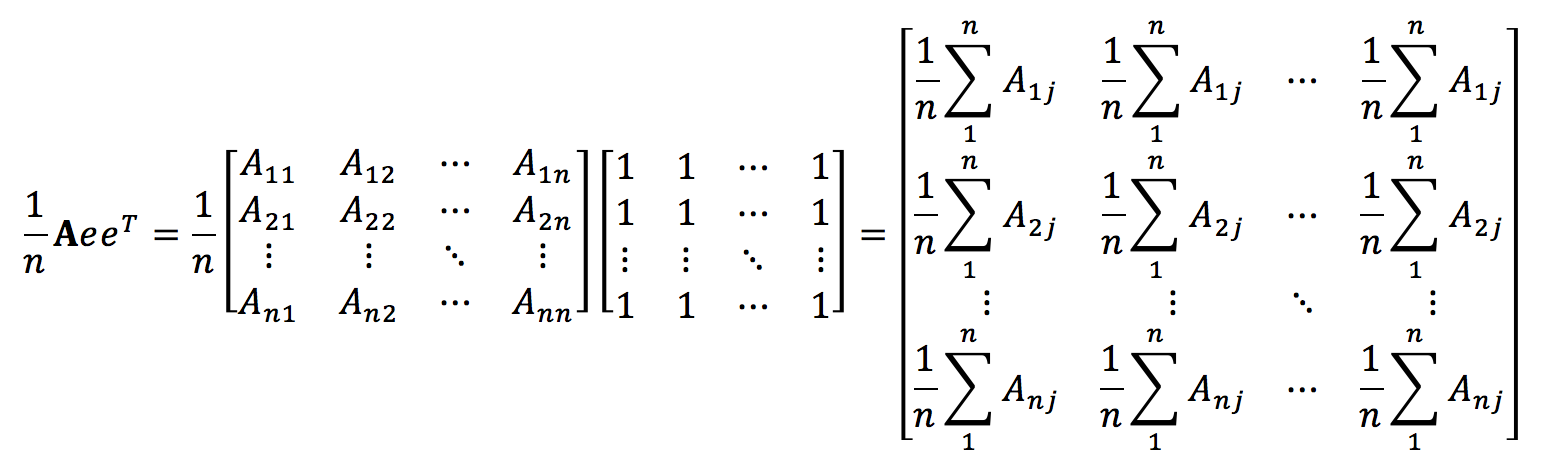
现在让我们来做平移，从而使得矩阵D^X中的点具有zero mean，注意平移操作并不会改变X中各个点的相对关系。为了便于理解，我们先来考察一下Aee^T/n和ee^TA/n的意义，其中A是一个n×n的方阵。

不难发现Aee^T/n中第i行的每个元素都是A中第i行的均值，类似的，我们还可以知道，ee^TA/n中第i列的每个元素都是A中第i列的均值。因此，我可以定义centering matrix H如下

所以D^XH的作用就是从D^X中的每个元素里减去列均值，HD^XH的作用就是在此基础上再从DX每个元素里又减去了行均值，因此centering matrix的作用就是把元素分布的中心平移到坐标原点，从而实现zero mean的效果。更重要的是，Let D be a distance matrix, one can transform it to an inner product matrix （Kernel Matrix） by K=-HDH/2, 即

上一步之所以成立，因为

因为B^X是一个内积矩阵（Gram Matrix/Kernel Matrix），所以它是对称的，这样一来，它就可以被对角化，即B^X=U∑U^T。

而我们的最终目的是find a concrete set of n points (Y) in k dimensions so that the pairwise Euclidean distances between all the pairs in the concrete set Y is a close approximation to the pair-wise distances given to us in the matrix D^X i.e. we want to find D^Y such that

Note that after applying the ”double centering” operation to both X and Y，上式服从

最终这个问题的解就是Y=U∑^1/2。

下面我们首先来演示在MATLAB中计算上述MDS问题的过程，为了展示其原理，下面的代码并不会直接使用MATLAB中内置的用于求解MDS的现成函数。

>> D = [[0,587,1212,701,1936,604,748,2139,2182,543],
[587,0,920,940,1745,1188,713,1858,1737,597],
[1212,920,0,879,831,1726,1631,949,1021,1494],
[701,940,879,0,1374,968,1420,1645,1891,1220],
[1936,1745,831,1374,0,2339,2451,347,959,2300],
[604,1188,1726,968,2339,0,1092,2594,2734,923],
[748,713,1631,1420,2451,1092,0,2571,2408,205],
[2139,1858,949,1645,347,2594,2571,0,678,2442],
[2182,1737,1021,1891,959,2734,2408,678,0,2329],
[543,597,1494,1220,2300,923,205,2442,2329,0]];

>> DSquare = D.^2;
>> H = eye(10)-ones(10)/10;
>> K = -0.5*H*DSquare*H;

>> [eigVec, eigVal] = eig(K);

>> Y = eigVec(:,1:2)*sqrt(eigVal(1:2,1:2))

Y =

   1.0e+03 *

    0.7188   -0.1430
    0.3821    0.3408
   -0.4816    0.0253
    0.1615   -0.5728
   -1.2037   -0.3901
    1.1335   -0.5819
    1.0722    0.5190
   -1.4206   -0.1126
   -1.3417    0.5797
    0.9796    0.3355

最后，我们在给出R中实现的示例代码，同样这里我们不会调用R中内置的用于求解MDS的现成函数。

> data.csv = read.csv("/Users/fzuo/Desktop/data.csv", header = T, row.names = 1)
> D <- as.matrix(data.csv)
> DSqure = D^2
> H = diag(10) - matrix(rep(1,100), nrow = 10)/10
> K = -0.5*H%*%DSqure%*%H
> result = eigen(K, symmetric = FALSE)
> vals = c(result$values[1],result$values[2])
> result$vectors[,1:2] %*% diag(sqrt(vals))
            [,1]       [,2]
 [1,]   718.7594 -142.99427
 [2,]   382.0558  340.83962
 [3,]  -481.6023   25.28504
 [4,]   161.4663 -572.76991
 [5,] -1203.7380 -390.10029
 [6,]  1133.5271 -581.90731
 [7,]  1072.2357  519.02423
 [8,] -1420.6033 -112.58920
 [9,] -1341.7225  579.73928
[10,]   979.6220  335.47281

可见，这和之前MATLAB中得到的结果是一致的。不仅如此，你还可以验证这与R中的内置函数cmdscale()所算出结果仍然保持一致（可能正负号相反，但这并无影响）。

参考文献

【1】http://www.cs.umd.edu/~djacobs/CMSC828/MDSexplain.pdf

详解多维标度法（MDS，Multidimensional scaling）

猜你喜欢