时序算法—AR、MA、ARMA和ARIMA模型以及Auto ARIMA

文章目录

引言

时间序列分析的目的是给定一个已被观测了的时间序列，预测该序列的未来值。ARIMA模型系列模型常用于基于时间序列的短期预测。为方便后面理解，这里简单介绍拖尾与截尾的含义。

截尾是指时间序列的自相关函数（ACF）或偏自相关函数（PACF）在某阶后均为0的性质（比如AR的PACF）
拖尾是ACF或PACF并不在某阶后均为0的性质（比如AR的ACF）

这里简单介绍时序模型算法中常用的函数

一、模型介绍

1.AR模型

AR模型又称为 $p$ 阶自回归模型，记 $A R (p)$ 。即在 $t$ 时刻的随机变量 $X_t$ 的取值 $x_t$ 是前 $p$ 期 $x_{t-1},x_{t-2},...,x_{t-p}$ 的多元线性回归。 $x_t$ 受过去 $p$ 期的序列值的影响。误差项是当期的随机干扰 $ε_t$ ,为零均值白噪声序列。
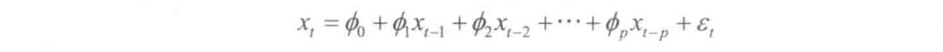
在这里插入图片描述
平稳AR模型的性质：

2.MA模型

MA模型又称为 $q$ 阶移动平均模型，记 $M A (q)$ 。即在 $t$ 时刻的随机变量 $X_t$ 的取值 $x_t$ 是前 $q$ 期 $随机扰动ε_{t-1},ε_{t-2},...,ε_{t-p}$ 的多元线性回归。 $x_t$ 受过去 $q$ 期的误差项的影响。误差项是当期的随机干扰 $ε_t$ ,为零均值白噪声序列。
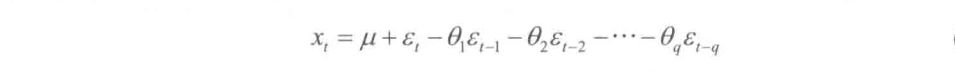
在这里插入图片描述
平稳MA模型的性质：

3.ARMA模型

ARMA模型又称为自回归移动平均模型，记 $A R M A (p, q)$ 。即在 $t$ 时刻的随机变量 $X_t$ 的取值 $x_t$ 是前 $p$ 期 $x_{t-1},x_{t-2},...,x_{t-p}$ 和前 $q$ 期 $随机扰动ε_{t-1},ε_{t-2},...,ε_{t-p}$ 的多元线性回归。 $x_t$ 受过去 $q$ 期的误差项和过去 $p$ 期的序列值的共同影响。误差项是当期的随机干扰 $ε_t$ ,为零均值白噪声序列。
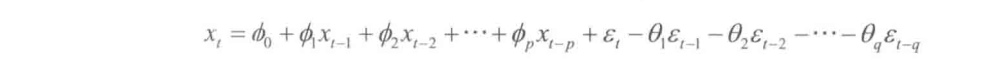
在这里插入图片描述
平稳 $A R M A (p, q)$ 模型的性质

ARMA模型识别原则：

4.ARIMA模型

以上的AR模型、MA模型、ARMA模型都是针对平稳非白噪声序列进行建模，但实际上自然界大部分序列都是非平稳的，ARIMA模型正是对非平稳时间序列进行建模。ARIMA模型的实质是差分运算与ARMA模型的组合。差分运算具有强大的确定性信息提取能力，许多非平稳序列差分后会显示出平稳序列的性质。

二、ARIMA建模流程

以餐厅的销售数据为例，链接：数据—百度网盘提取码：1234

1.第一步：获得观察值序列并平稳性检验

平稳性检验有两种方法：一种是根据时序图与自相关图进行主观的图检验，另一种是构造检验统计量来进行统计，目前最常用的方法是单方根检验。

import pandas as pd
import matplotlib.pyplot as plt

# 加载数据
data = pd.read_excel('data/arima_data.xls', index_col=0)

时序图与自相关图检验

时序图

"""
1.画时序图
"""
# 用于解决中文
plt.rcParams['font.sans-serif'] = [u'simHei']
# 用于解决负号
plt.rcParams['axes.unicode_minus'] = False
data.plot(style='ro-')
plt.show()

在这里插入图片描述
由于平稳时间序列的均值与方差均为常数，这也意味着平稳序列的时序图会显示该序列始终在常数附近波动，而且波动的范围有界。如果表现出明显的趋势性或者周期性，那么该序列就不是平稳序列。由图可知，该序列很明显呈上升趋势。
自相关图

"""
2.自相关图
"""
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
plot_acf(data).show()

在这里插入图片描述
平稳序列只有短期相关性，随着延迟期数k的增加，平稳序列的自相关系数会很快的趋近于0，并在零附近随机波动。而非平稳序列的自相关系数衰减的速度比较慢。由图可知，该序列自相关系数衰减速度慢

单方根检验
单方根检验是指检验序列中是否存在单方根，存在单方根就是非平稳时间序列

"""
单方根检验
"""
from statsmodels.tsa.stattools import adfuller as ADF
print("原始序列的ADF检验结果为:", ADF(data['销量']))

返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore
原始序列的ADF检验结果为: (1.8137710150945274, 0.9983759421514264, 10, 26, {
    
    '1%': -3.7112123008648155, 
'5%': -2.981246804733728, '10%': -2.6300945562130176}, 299.46989866024177)

由于原始序列是非平稳序列，所以进行差分运算后在进行平稳性检验

2.第二步：一阶差分并平稳性检验

许多非平稳序列差分后会显示出平稳序列的性质,这里尝试一阶差分

# 一阶差分
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']

# 时序图
D_data.plot()
plt.show()

在这里插入图片描述
发现它没有明显的上升（下降）趋势或者周期趋势，在均值附近进行平稳的波动。

# 自相关图
plot_acf(D_data).show()

在这里插入图片描述
自相关图有很强的短期相关性（近期的序列值对现时值影响比较明显）

# 单方根检验
print(u'差分序列的ADF检验结果为：', ADF(D_data[u'销量差分']))

差分序列的ADF检验结果为： (-3.1560562366723532, 0.02267343544004886, 0, 35, {
    
    '1%': -3.6327426647230316, 
'5%': -2.9485102040816327, '10%': -2.6130173469387756}, 287.5909090780334)

单方根检验p值小于0.05.综上所述，经过一阶差分后，非平稳序列变成平稳序列。

3.第三步：白噪声检验

# 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
# 返回统计量与p值
print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1, return_df=True))

# 1是索引
1 11.304022   0.000773

由于输出的p值远小于0.05,通过P<α,拒绝原假设，所以一阶差分后的序列是平稳非白噪声序列，如若不满足白噪声检验，则分析结束

4.第四步：模型定阶

这里采用相对最优模型识别方法，计算 $p$ 和 $q$ 的所有组合的 $B I C$ 信息量，取其中BIC信息量达到最小的模型阶数，还可以使用如下准则
在这里插入图片描述

from statsmodels.tsa.arima_model import ARIMA

# 定阶
data[u'销量'] = data[u'销量'].astype(float)
pmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
qmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
bic_matrix = []
for p in range(pmax + 1):
    tmp = []
    for q in range(qmax + 1):
        try:  # 存在部分报错，所以用try来跳过报错。
            tmp.append(ARIMA(data, (p, 1, q)).fit().bic)
        except:
            tmp.append(None)
    bic_matrix.append(tmp)

bic_matrix = pd.DataFrame(bic_matrix)  # 从中可以找出最小值

# 先用stack展平，然后用idxmin找出最小值位置。
p, q = bic_matrix.stack().idxmin()
print(u'BIC最小的p值和q值为：%s、%s' % (p, q))

BIC最小的p值和q值为：0、1

$p 、 q$ 定阶完成，即对原始序列建立ARIMA(0,1,1)模型。

5.第五步：建立模型

# 建立ARIMA(0, 1, 1)模型
model = ARIMA(data, (p, 1, q)).fit()  
print('模型报告为：\n', model.summary2())
print('预测未来5天，其预测结果、标准误差、置信区间如下：\n', model.forecast(5))

                            Results: ARIMA
====================================================================
Model:              ARIMA            BIC:                 422.5101  
Dependent Variable: D.销量             Log-Likelihood:      -205.88   
Date:               2021-04-02 21:48 Scale:               1.0000    
No. Observations:   36               Method:              css-mle   
Df Model:           2                Sample:              01-02-2015
Df Residuals:       34                                    02-06-2015
Converged:          1.0000           S.D. of innovations: 73.086    
No. Iterations:     23.0000          HQIC:                419.418   
AIC:                417.7595                                        
----------------------------------------------------------------------
               Coef.    Std.Err.     t      P>|t|     [0.025    0.975]
----------------------------------------------------------------------
const         49.9555    20.1390   2.4805   0.0131   10.4837   89.4272
ma.L1.D.销量     0.6710     0.1648   4.0712   0.0000    0.3480    0.9941
-----------------------------------------------------------------------------
                 Real           Imaginary          Modulus          Frequency
-----------------------------------------------------------------------------
MA.1           -1.4902             0.0000           1.4902             0.5000
====================================================================

预测未来5天，其预测结果、标准误差、置信区间如下：
 (array([4873.96635877, 4923.92182229, 4973.8772858 , 5023.83274931,
       5073.78821282]), array([ 73.08573849, 142.32690305, 187.54298039, 223.80301976,
       254.95727841]), array([[4730.72094356, 5017.21177399],
       [4644.96621828, 5202.87742629],
       [4606.29979868, 5341.45477291],
       [4585.18689095, 5462.47860767],
       [4574.08112954, 5573.49529611]]))

6.第六步:白噪声检验

----------------------------------------------------------------------
               Coef.    Std.Err.     t      P>|t|     [0.025    0.975]
----------------------------------------------------------------------
const         49.9555    20.1390   2.4805   0.0131   10.4837   89.4272
ma.L1.D.销量     0.6710     0.1648   4.0712   0.0000    0.3480    0.9941
-----------------------------------------------------------------------------

由于P=0.0000 ，P<α=0.05，拒绝原假设，认为该模型ARIMA(0,1,1)拟合该序列，残差序列已实现白噪声

7.完整代码

import pandas as pd
import matplotlib.pyplot as plt

# 加载数据
data = pd.read_excel('data/arima_data.xls', index_col=0)

"""
画时序图
"""
# 用于解决中文
plt.rcParams['font.sans-serif'] = [u'simHei']
# 用于解决负号
plt.rcParams['axes.unicode_minus'] = False
data.plot(style='ro-')
plt.show()

"""
自相关图
"""
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

plot_acf(data).show()

"""
单方根检验
"""
from statsmodels.tsa.stattools import adfuller as ADF

print("原始序列的ADF检验结果为:", ADF(data['销量']))

# 一阶差分
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
# 时序图
D_data.plot()
plt.show()
# 自相关图
plot_acf(D_data).show()
# 偏自相关图
plot_pacf(D_data).show()
# 单方根检验
print(u'差分序列的ADF检验结果为：', ADF(D_data[u'销量差分']))

# 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox

# 返回统计量与p值
print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1, return_df=True))

from statsmodels.tsa.arima_model import ARIMA

# 定阶
data[u'销量'] = data[u'销量'].astype(float)
pmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
qmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
bic_matrix = []
for p in range(pmax + 1):
    tmp = []
    for q in range(qmax + 1):
        try:  # 存在部分报错，所以用try来跳过报错。
            tmp.append(ARIMA(data, (p, 1, q)).fit().bic)
        except:
            tmp.append(None)
    bic_matrix.append(tmp)

bic_matrix = pd.DataFrame(bic_matrix)  # 从中可以找出最小值

# 先用stack展平，然后用idxmin找出最小值位置。
p, q = bic_matrix.stack().idxmin()
print(u'BIC最小的p值和q值为：%s、%s' % (p, q))

# 建立ARIMA(0, 1, 1)模型
model = ARIMA(data, (p, 1, q)).fit()
print('模型报告为：\n', model.summary2())
print('预测未来5天，其预测结果、标准误差、置信区间如下：\n', model.forecast(5))

三、Auto ARIMA

ARIMA是一个非常强大的时间序列预测模型，但是数据准备与参数调整过程非常耗时
Auto ARIMA让整个任务变得非常简单，舍去了序列平稳化，确定d值，创建ACF值和PACF图，确定p值和q值的过程

Auto ARIMA的步骤:

加载数据并进行数据处理，修改成时间索引
预处理数据:输入的应该是单变量，因此需要删除其他列
拟合Auto ARIMA，在单变量序列上拟合模型
在验证集上进行预测
计算RMSE:用验证集上的预测值和实际值检查RMSE值

Auto-ARIMA通过进行差分测试,来确定差分d的顺序，然后在定义的start_p、max_p、start_q、max_q范围内拟合模型。如果季节可选选项被启用，auto-ARIMA还会在进行Canova-Hansen测试以确定季节差分的最优顺序D后，寻找最优的P和Q超参数。
为了找到最好的模型,给定information_criterion auto-ARIMA优化,(‘aic’,‘aicc’,‘bic’,‘hqic’,‘oob’)
并返回ARIMA的最小值。
注意，由于平稳性问题，auto-ARIMA可能无法找到合适的收敛模型。如果是这种情况，将抛出一个ValueError，建议在重新拟合之前使数据变稳定，或者选择一个新的顺序值范围。

1.常用参数介绍

pmdarima.arima.auto_arima

1.start_p:p的起始值，自回归(“AR”)模型的阶数(或滞后时间的数量),必须是正整数
2.start_q:q的初始值，移动平均(MA)模型的阶数。必须是正整数。
3.max_p:p的最大值，必须是大于或等于start_p的正整数。
4.max_q:q的最大值，必须是一个大于start_q的正整数
5.seasonal:是否适合季节性ARIMA。默认是正确的。注意，如果season为真，而m == 1，则season将设置为False。
6.stationary :时间序列是否平稳，d是否为零。
6.information_criterion：信息准则用于选择最佳的ARIMA模型。(‘aic’，‘bic’，‘hqic’，‘oob’)之一
7.alpha：检验水平的检验显著性，默认0.05
8.test:如果stationary为假且d为None，用来检测平稳性的单位根检验的类型。默认为‘kpss’;可设置为adf
9.n_jobs ：网格搜索中并行拟合的模型数(逐步=False)。默认值是1，但是-1可以用来表示“尽可能多”。
10.suppress_warnings：statsmodel中可能会抛出许多警告。如果suppress_warnings为真，那么来自ARIMA的所有警告都将被压制
11.error_action:如果由于某种原因无法匹配ARIMA，则可以控制错误处理行为。(warn,raise,ignore,trace)
12.max_d:d的最大值，即非季节差异的最大数量。必须是大于或等于d的正整数。
13.trace:是否打印适合的状态。如果值为False，则不会打印任何调试信息。值为真会打印一些

2.案例

数据—百度链接提取码：1234

import warnings
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from datetime import datetime
from math import sqrt
from sklearn.metrics import mean_squared_error
from pmdarima.arima import auto_arima


def main():
    warnings.filterwarnings(action='ignore')
    # 第一步:加载数据
    # 定义将字符串时间转化成日期时间数组
    date_parser = lambda dates: datetime.strptime(dates, '%Y/%m/%d')
    data = pd.read_csv('../data/Data.csv', header=0, parse_dates=['month'], date_parser=date_parser, index_col='month')
    data.fillna(method='pad', inplace=True)
    # print(data.head(5))
    # print(data.index)
    # print(data.dtypes)

    # 第二步：预处理数据-由于所给数据本身就是单变量序列，并且没有空值，因此，可以不进行这一步处理
    # 将数据分成训练集与验证集
    val_size = 10
    train_size = 10 * val_size
    train, val = data[-(train_size + val_size):-val_size + 1]['data'], data[-val_size:]['data']
    # plot the data
    fig = plt.figure()
    fig.add_subplot()
    plt.plot(train, 'r-', label='train_data')
    plt.plot(val, 'y-', label='val_data')
    plt.legend(loc='best')
    plt.show(block=False)

    # 第三步:buliding the model
    # 仅需要fit命令来拟合模型,而不必要选择p、d、q的组合，模型会生成AIC值和BIC值，以确定参数的最佳组合
    # AIC和 BIC是用于比较模型的评估器，这些值越低，模型就越好
    model = auto_arima(train, start_p=0, start_q=0, max_p=6, max_q=6, max_d=2,
                       seasonal=True, test='adf',
                       error_action='ignore',
                       information_criterion='aic',
                       njob=-1, trace=True, suppress_warnings=True)
    model.fit(train)

    # 第四步:在验证集上进行预测
    forecast = model.predict(n_periods=len(val))
    print(forecast)
    forecast = pd.DataFrame(forecast, index=val.index, columns=['prediction'])

    # calculate rmse
    rmse = np.sqrt(mean_squared_error(val, forecast))
    print('RMSE : %.4f' % rmse)

    # plot predictions
    fig = plt.figure()
    fig.add_subplot()
    plt.plot(train, 'r-', label='train')
    plt.plot(val, 'y-', label='val')
    plt.plot(forecast, 'b-', label='prediction')
    plt.legend(loc='best')
    plt.title('RMSE : %.4f' % rmse)
    plt.show(block=False)


if __name__ == '__main__':
    main()

如果对您有帮助，麻烦点赞关注，这真的对我很重要！！！如果需要互关，请评论区留言或私信！
在这里插入图片描述