Python构建ARIMA模型

1 可视化分析

1.1 空气质量和空气检测成分分析

import pandas as pd
from statsmodels.stats.diagnostic import acorr_ljungbox # 白噪声检验

filename = r'C:\Users\Administrator\Desktop\data.csv'
data = pd.read_csv(filename)
plt.rcParams['font.sans-serif'] = ['SimHei']  ##能显示中文
sns.catplot(x='质量等级', y='SO2', kind='box',data=data)
plt.title('SO2和质量等级的箱线图')

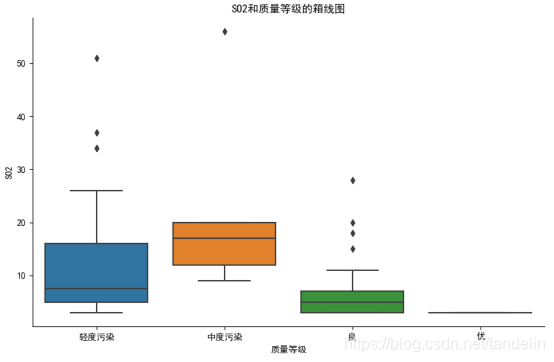
由上图可知，在中度污染时，SO2的中位数含量高于污染程度为优的含量，有理由认为SO2的含量对空气质量影响不大。
-------------------------------------------根据以上原理，分别做其它空气成分含量图。--------------

1.2 不同时间段空气质量下的空气含量成分分析

为了进一步探究连续不同时间段空气质量下的空气含量成分分析，对空气质量、时间、成分进行对比筛选，分析如下：

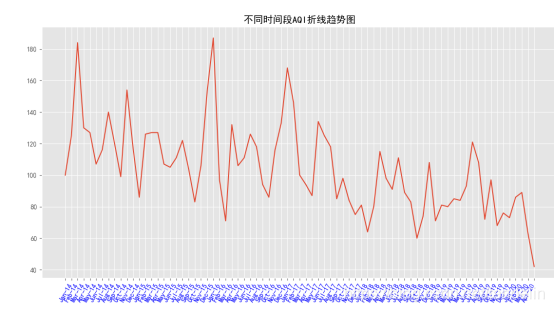
1.3 季节和空气成分含量分析

plt.rcParams['font.sans-serif'] = ['SimHei']
sns.catplot(x='季节', y='SO2', kind='box',data=data)
plt.title('SO2和季节的箱线图')

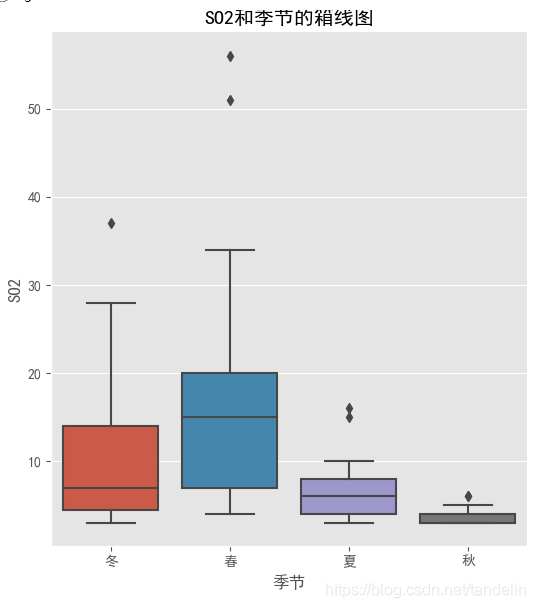
2 时间序列ARIMA模型分析

2.1 ARMA模型概述

ARMA模全称为自回归移动平均模型(Auto-regressive Moving Average Model，简称 ARMA)是研究时间序列的重要方法。其在经济预测过程中既考虑了经济现象在时间序列上的依存性, 又考虑了随机波动的干扰性, 对经济运行短期趋势的预测准确率较高, 是近年应用比较广泛的方法之一。ARMA模型是由美国统计学家G.E.P.Box 和 G.M.Jenkins在20世纪70年代提出的著名时序分析模型,即自回归移动平均模型。ARMA模型有自回归模型AR(q)、移动平均模型MR(q)、自回归移动平均模型ARMA(p,q) 3种基本类型。其中ARMA(p,q）自回归移动平均模型，模型可表示为：

其中，为自回归模型的阶数，为移动平均模型的介数；表示时间序列在时刻的值；为自回归系数；表示移动平均系数；表示时间序列在时期的误差或偏差。
2.2 趋势分析和单位根检验
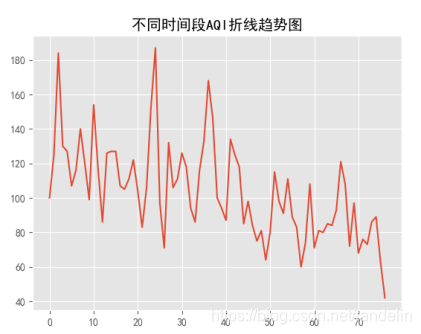
对AQI进行时序图的折线分析如下，发现AQI具备一定的下降趋势，时间序列数据不够平稳，因此对数据进行一阶差分。
plt.plot(data[u’AQI’])
plt.title(‘不同时间段AQI折线趋势图’)

一阶差分后的时序图

AQIdata=data[u’AQI’]
D_data = AQIdata.diff().dropna()
plt.plot(D_data)
plt.title(‘一阶差分后不同时间段AQI折线趋势图’)

由上图可知，一阶差分后数据趋于稳定，因此对数据进一步进行ADF单位根检验，得出检验水平如下：
print(u’差分序列的白噪声检验结果为：’, acorr_ljungbox(D_data, lags=1))

一阶差分的AQI单位根检验
t-Statistic Prob1*
Augmented Dickey- Fuller Test Statistic -6.214 0.0000
Test Critical Values 1% level -3.527
5% level -2.903
10% level -2.589
print(‘一阶差分序列的检验结果为：’,adfuller(D_data))

由相伴概率知，P远远小于0，01，因此认为序列是平稳的。
2.3模型的识别与选择
计算出样本自相关系数和偏相关系数的值之后，我们主要是根据它们表现出来的性质，选择适当的ARMA模型拟合观察值序列。这个过程实际上就是要根据样本自相关系数和偏相关系数的性质估计自相关阶数 和移动平均阶数，因此模型的识别过程也成为定阶过程。一般ARMA模型定阶的基本原则如表2示：

表2 ARMA(p,q)模型选择原则
ACF PACF 模型定阶
拖尾 p阶截尾 AR§模型
q阶截尾 拖尾 MA(q)模型
拖尾 拖尾 ARMA(p,q)模型

利用Python对差分数据进行操作，可得样本自相关系数和偏相关系数图如图所示：


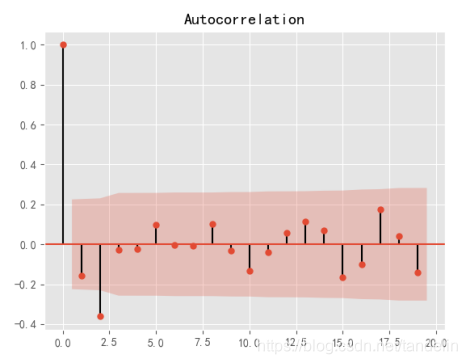
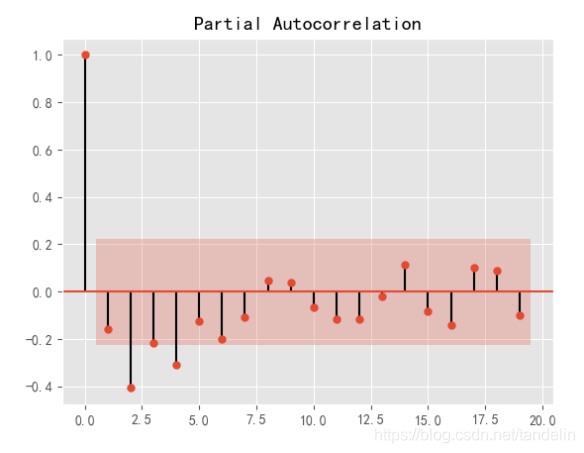
通过对一阶差分的对数序列的自相关系数和偏相关系数图的分析观察，可以知道模型大致可选取两种模型。第一种，自相关系数为拖尾，而偏相关系数为一阶截尾。此时选取模型可以为ARIMA（1,1,2）模型。第二种，自相关二阶截尾，而偏相关系数为一阶截尾。此时选取模型可以为ARIMA(2,1,1）模型。
2.4参数估计
选择拟合好后的模型之后，下一步就是要利用序列的观察值确定该模型的口径，即估计模型中未知参数的值。对于一个非中心化ARMA（p,q）模型，有
式中，

该模型共含个未知参数：。对于未知参数的估计方法有三种：矩估计﹑极大似然估计和最小二乘估计。其中本文使用最小二乘估计法对序列进行参数估计。
在ARMA(p,q)模型场合，记

残差项为：

残差平方和为：

是残差平方和达到最小的那组参数值即为的最小估计值。
使用Python操作可得序列两种可能的参数估计图如下图所示：

fit model

from pandas import read_csv
from pandas import datetime
from pandas import DataFrame
from statsmodels.tsa.arima_model import ARIMA
from matplotlib import pyplot

import pandas as pd
filename = r'C:\Users\Administrator\Desktop\data.csv'
data = pd.read_csv(filename)
model = ARIMA(data.AQI, order=(2,1,1))
model_fit = model.fit(disp=0)
print(model_fit.summary())

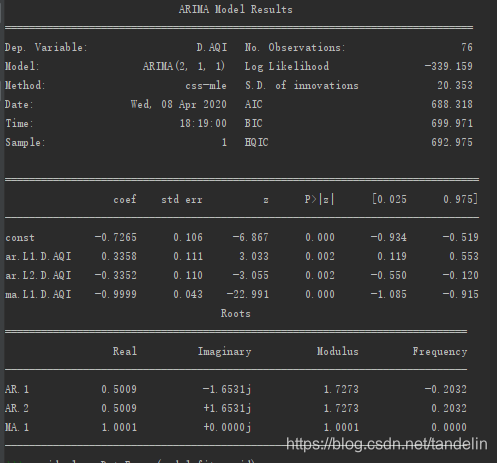
模型结果如下：

假设AQI用Y表示，则

model = ARIMA(data.AQI, order=(1,1,2))
model_fit = model.fit(disp=0)
print(model_fit.summary())

通过毕竟AIC和BIC选择模型ARIMA(2,1,1).得到模型的表达公式结果为：

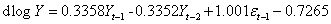
# plot residual errors


residuals = DataFrame(model_fit.resid)
residuals.plot()
pyplot.show()
residuals.plot(kind='kde')
pyplot.show()
print(residuals.describe())