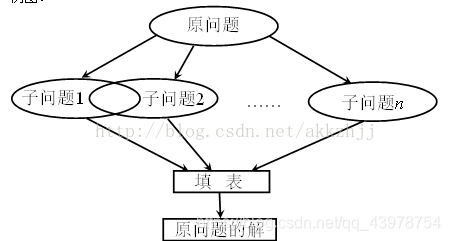
动态规划问题dp问题以及经典问题

动态规划

其实他的思想跟分治还是很像的，都是分成子问题求最优解最后合并推出总体的最优解。但不同的是，如果分解的子问题有很多是相同的，采用分治法相同的子问题会求解多次，是不是很影响效率；动态规划法呢，它会保存已解决的子问题的答案，再有相同的子问题直接用保存的答案就行了，节省了很多计算时间。

图片来源

动态规划和分治都是将大问题划分为小问题，小问题间独立是分治，小问题间有状态关系，并且需要用到之前状态是动态规划，不需要的是贪心法。

经典问题有找硬币，爬楼梯

（1）硬币找零：

给予不同面值的硬币若干种种（每种硬币个数无限多），如何用若干种硬币组合为某种面额的钱，使硬币的的个数最少？
在现实生活中，我们往往使用的是贪心算法，比如找零时需要13元，我们先找10元，再找2元，再找1元。如果我们的零钱可用的有1、2、5、9、10。我们找零18元时，贪心算法的策略是：10+5+2+1，四种，但是明明可以用两个9元的啊。这种问题一般使用动态规划来解决。

这是力扣上一个大佬的代码，dfs+剪枝

class Solution {
    
    
    public int coinChange(int[] coins, int amount) {
    
    
        Arrays.sort(coins);
        recursion(coins, amount, 0, coins.length - 1);
        return minCount == Integer.MAX_VALUE ? -1 : minCount;
    }
    int minCount = Integer.MAX_VALUE;
    /**
     * 1、按金额从大到小，从多到少（排序，用余数一步到位）
     * 2、预判低于最优解，终止递归（可以返回最优解，不过提升有限，意义不大）
     * 3、能整除即可返回
     */
    void recursion(int[] coins, int amount, int count, int index) {
    
    
        if (index < 0 || count + amount / coins[index] >= minCount) return;
        if (amount % coins[index] == 0) {
    
    
            minCount = Math.min(minCount, count + amount / coins[index]);
            return;
        }
        for (int i = amount / coins[index]; i >= 0; i--) {
    
    
            recursion(coins, amount - i * coins[index], count + i, index - 1);
        }
    }
}

（2）爬楼梯：

有一段连续的楼梯，共n阶台阶。要从楼梯底部向上爬到楼梯顶部。她可以一次迈一阶台阶，也可以一次迈两阶台阶（但绝对不会向下退回）。问她一共有多少种不同的爬楼梯方式?

说实话，这种思想真的跟高中求解从n个人里面选m个人有多少种选法一样，假设问题可分解成m个人里面一定有班长+m个人里面没有班长。接着可以递归再接着分。
以上楼梯最后一次选择为例，他可以是在第n-1阶一次走一阶上来也可以是在第n-2阶一次走两阶上来，l两种可能性相加即为总的可能性，所以问题可以转变成T(n)=T(n-1)+T(n-2)，可以递归往前推，公式与斐波那契定律一样。

不用递归做这一题时间复杂度为O(n),空间复杂度为O(1)。

//删去#那些库了，你们可以自己加上
int main()
{
    
    
	int a1, a2;
	int n = 10;
	a1 = 1; 
	a2 = 1;
	for (int i = 1; i < n; i++)
	{
    
    
		int temp = a2;
		a2 = a1 + a2;
		a1 = temp;
	}
	cout << a2;
}