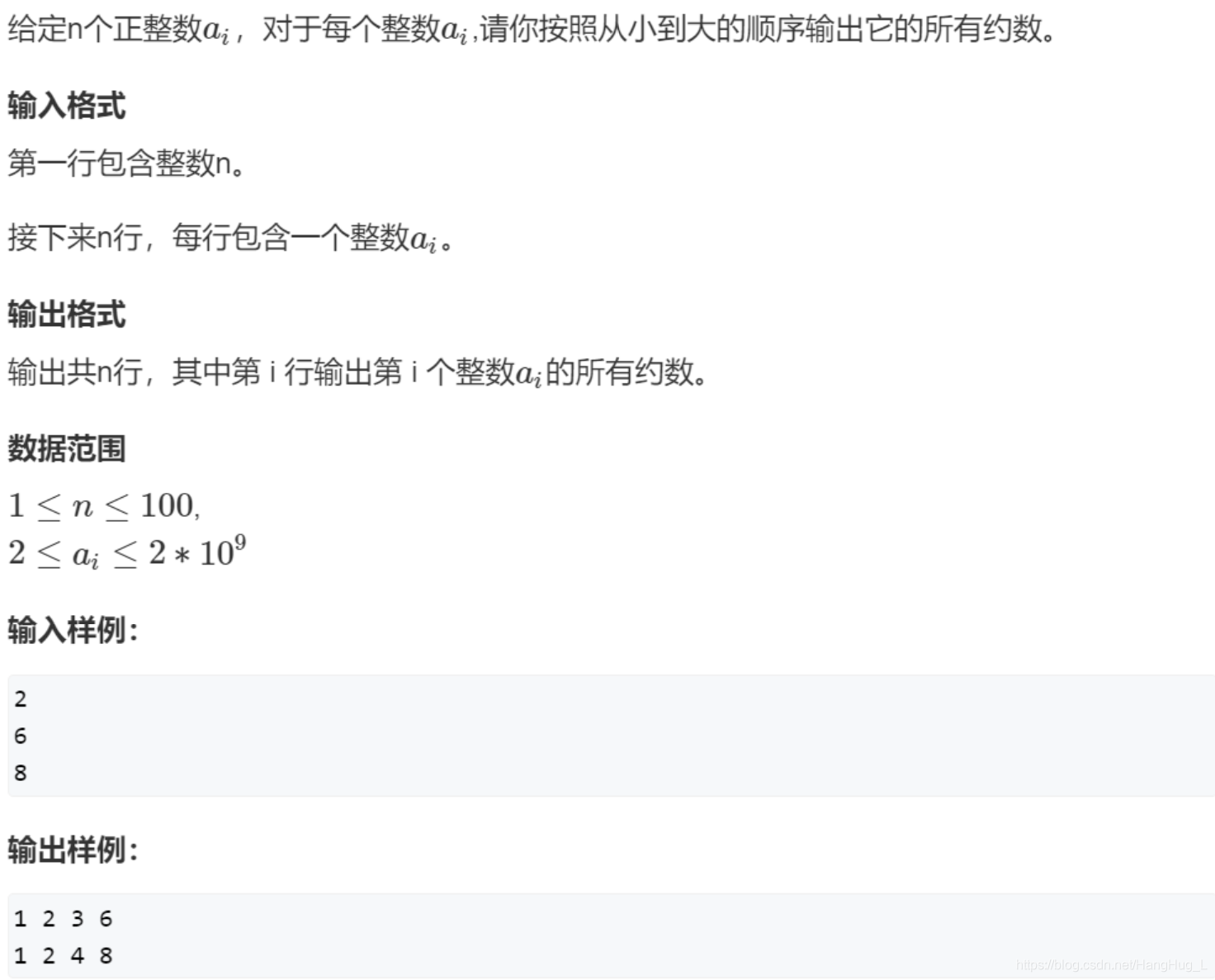
1. 试除法求约数
#include <iostream>
#include <vector>
#include <algorithm>
#define read(x) scanf("%d",&x)
using namespace std;
vector<int> getDivisors(int x)
{
vector<int> res;
for (int i=1;i<=x/i;i++) {
if (x%i==0) {
res.push_back(i);
if (i!=x/i) res.push_back(x/i);
}
}
sort(res.begin(),res.end());
return res;
}
int main()
{
int n,x;
read(n);
while (n--) {
read(x);
vector<int> res=getDivisors(x);
for (int t:res) printf("%d ",t); //仅适用于Stl容器的遍历
puts("");
}
return 0;
}
假设N的质因数分解,N=p1a1×p2a2×p3a3×……×pnan,p1到pn都是质数。
那么N的约数个数num=(a1+1)×(a2+1)×(a3+1)×……×(an+1)
N的约数之和sum=(p10+p11+p12+……×p1a1)×(p20+p21+p22+……×p2a2)×……× (pn0+pn1+pn2+……×pnan)
因此,2 和 3题都要涉及前面素数中的分解质因数的部分。
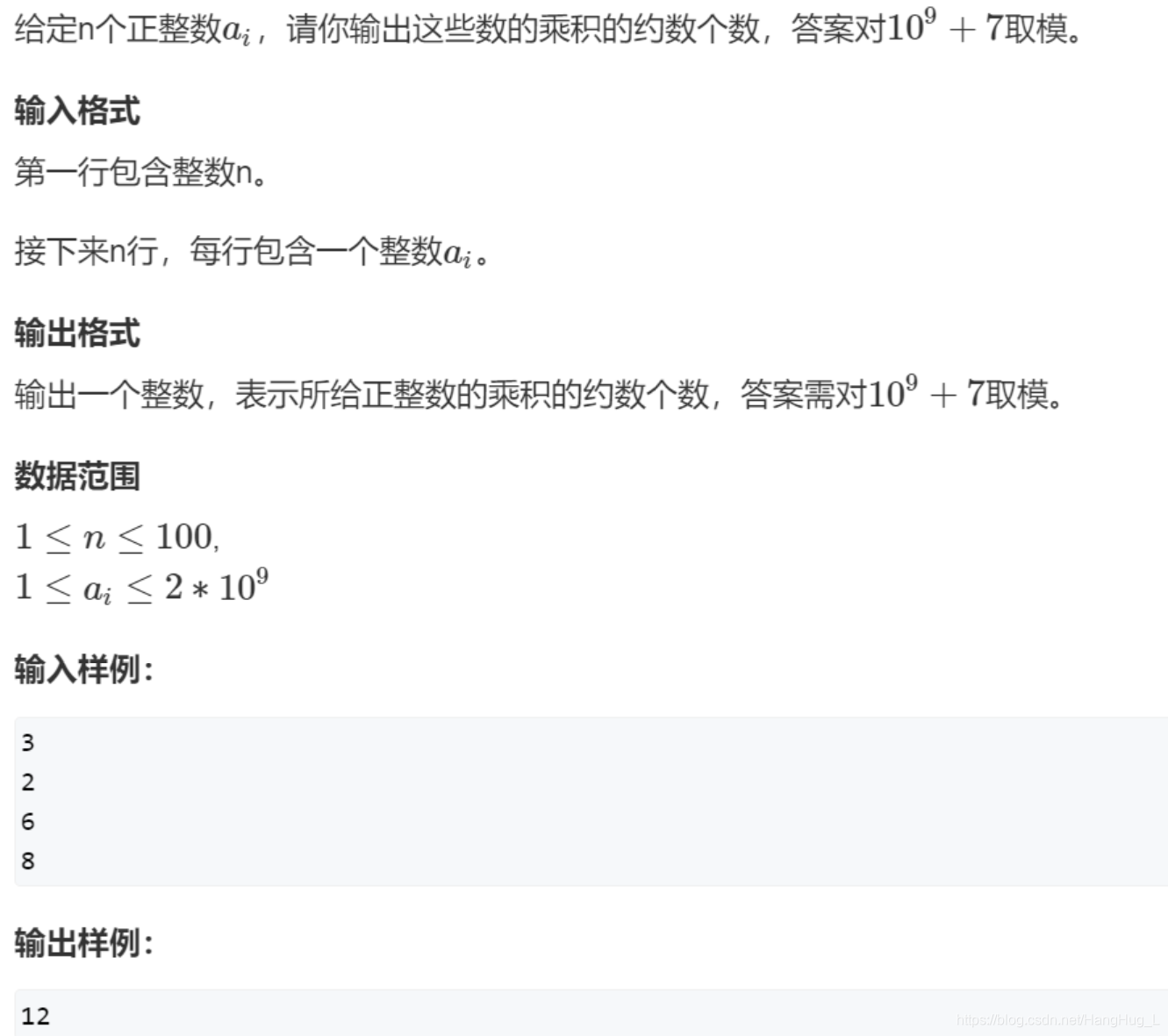
2. 求约数个数
取模
加法:
(a+b+c)%p == a%p + b%p + c%p,为了保险起见,如果a%p + b%p + c%p范围超过了p,写成(a%p + b%p + c%p) % p乘法:
(a×b×c)%p == a%p × b%p × c%p,同样为了防止数值超出p,写成:(a%p × b%p × c%p)%p
这里的N=a1×a2×……an,因此求出每个ai的分解质因数,不能存在数组里,下标是质因数,值是该质因数的个数,因为数值范围太大了,2e9,数组就算开在main函数也开不到1e9,1e8可以开,所以这里用哈希映射比较好,直接用map容器。
#include <iostream>
#include <unordered_map>
#define read(x) scanf("%d",&x)
#define ff first
#define ss second
using namespace std;
const int mod=1e9+7;
int main()
{
int n,x;
read(n);
unordered_map<int,int> hash;
while (n--) {
read(x);
//对x分解质因数,存在hash表中
for (int i=2;i<=x/i;i++)
while (x%i==0) x/=i,hash[i]++;
if (x>1) hash[x]++;
}
//开始求个数,注意map容器的遍历方法
long long res=1;
for (auto t:hash) res=(res*(t.ss+1))%mod;
printf("%d\n",res);
return 0;
}
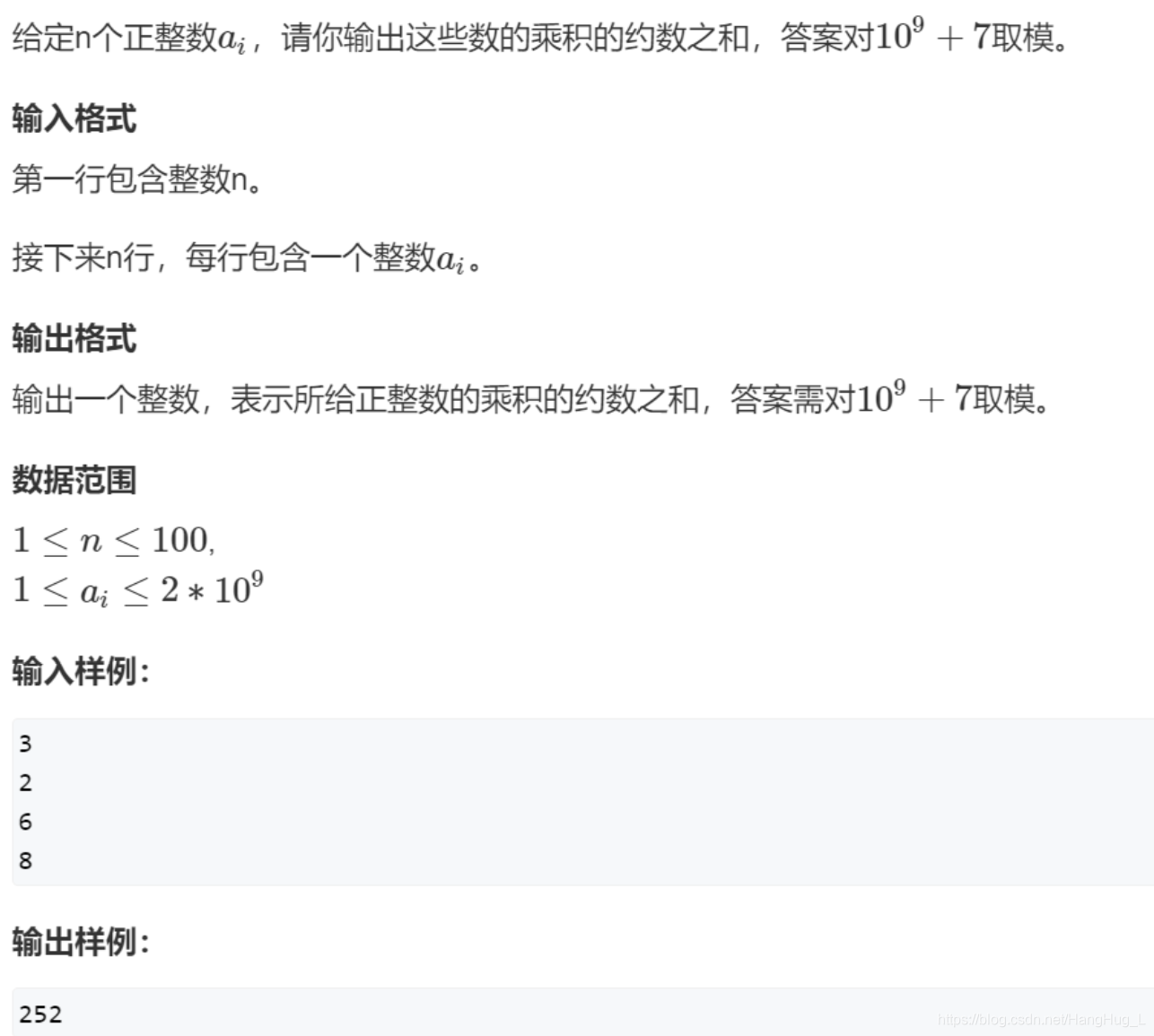
3. 求约数之和
求t=p0+p1+p2+……×pa的简便算法:
p3+p2+p+1可以写成p * (p2+p+1)+1,可以写成p * ( (p * (p+1)) +1) +1,根据这样的思想,
先初始化 t=1;
while(a--) t=t*p+1;
t=1,即为p0 =1
然后,
① t * p+1=p0 * p+1=p+1
② t * p+1=(p+1) * p +1 = p2+p+1
③ t * p+1=(p2+p+1) * p+1=p3+p2+p+1
#include <iostream>
#include <unordered_map>
#define read(x) scanf("%d",&x)
#define ff first
#define ss second
using namespace std;
const int mod=1e9+7;
int main()
{
int n,x;
read(n);
unordered_map<int,int> hash;
while (n--) {
//把n个数都分解质因数,累积起来了,相当于N本身了
read(x);
for (int i=2;i<=x/i;i++)
while (x%i==0) hash[i]++,x/=i;
if (x>1) hash[x]++;
}
long long res=1;
for (auto prime:hash) {
int p=prime.ff,a=prime.ss;
long long t= 1;
while (a--) t=(t*p+1)%mod;
res=(res*t)%mod;
}
printf("%d",res);
return 0;
}
第27 行的取模问题很迷惑?
写成,t=t*p+1;,不取模,就是错误的。
4. 最大公约数
d能整除a,记作d|a,即a=k×d。
推导:
求a和b的最大公因数,即d|a,d|b,求d的最大值。
有一个性质:若d|a,d|b,则d|x×a+y×b
假设d的最大值是s,且有a>b,即s|a,s|b,那么就有s | x×a+y×b,
令x=1,y=-k,则s | a-kb,其中k满足条件 k×b<=a,(k+1)×b>a
那么a-kb等价于a%b
所以有递推公式: gcd(a,b)=gcd(b,a%b),a>b,选最小的两个数求最小公约数,即b和a%b
当b为0时,递推就结束了,因为除数不能为0,此时的a就是最大公约数。
0 除以 任何一个数都得0 ,即可以整除,所以0与一个数的最大公约数是这个数本身;
0和0没有最大公约数。
递归模板:
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
最好这里的传参是a>=b,如果是小于的话,也没关系。
假如输入的是a=21,b=24,即求gcd(21,24);
那么a%b=21%24=21,b=24,然后就成了gcd(24,21); 这样就走上了正轨,只不过是多递归了一次。
非递归模板:
上面说到的b=0,那么就输出a,a就是最大公因数,第n次递归的b为0就是第n-1次递归传参的a%b==0,a就是第n-1次递归的b,所以在第n-1次递归时发生了a%b为0的情况就可以退出循环了,此时输出b即可。
if(a<b) swap(a,b);
int gcd(int a,int b)
{
if (b==0) return a;
int r=a%b;
while (r) {
a=b;
b=r;
r=a%b;
}
return b;
}
非递归模板必须要判断a和b的大小,满足a>=b;递归模板不需要。
非递归模板必须要特判一开始b为0的情况;递归模板不需要。
最小公倍数
lcm(a,b)=a*b/gcd(a,b);
但有时为了防止a * b超出定义的数据的范围,可以写成 lcm(a,b)=a/gcd(a,b)*b;
求n个数的最大公因数
int Gcds(int a[],int n) //数组从0到n-1
{
int res=a[0];
for (int i=1;i<n;i++) res=gcd(res,a[i]);
return res;
}
求n个数的最大公因数
int Lcms(int a[],int n) //数组从0到n-1
{
int res=a[0];
for (int i=1;i<n;i++) res=lcm(res,a[i]);
return res;
}