导数:
一个函数在某一点的导数描述了这个函数在这一点附近的变化趋势和变化率,以物体的上抛运行为例,其(位置-时间),(速度-时间),以及(加速度-时间)的曲线可以用下图表示:
其中(速度-时间)曲线是(位置-时间)曲线在每一点的导数的值的集合,同样道理,(加速度-时间)曲线是由(速度-时间)求导得到。
以图为例,一开始,位置的变化率比较快,反映的是速度曲线的速度值比较大,随着时间推进,位置曲线随时间的变化率逐渐变小,以至于最终达到最高点和水平x轴平行,速度则逐渐减小到0,标识速度逐渐趋于小以至于达到0,对应物体达到上抛物最高点速度变为0静止。
位置函数达到最高点后,速度变化率开始从小变大,对应速度曲线从0开始逐渐变大,符号标识方向和上抛相反,最终在4秒时刻,物体到达原来抛物位置。速度达到最大,也就是上抛给定的初始速度。
同样的分析,速度曲线是一条斜率为-2的直线,表示速度的变化率和变化趋势是-2,在整个过程中稳定变化,在物理里面有一个专门的名字描述它,叫做加速度。
所以加速度曲线是一个固定的常数值.
多元函数:
初等数学遇到的大部分是一元函数的情况,也就是导致因变量产生变化的因素只有一个,但大多数情况下,决定因变量的因素可能并非只有一个,以某个地区的房价为例,导致房价变动的因素还可能包括,面积,学区划分,地段,交通,城市规模等等。每个因素也可以作为自变量,自变量不为1个的函数叫做多元函数。
偏导数:
第一条说了,导数是函数值关于自变量的变化率,但是多元函数有多个自变量,每个自变量可以独立自由变化,那么它的函数值的变化率该如何得到呢?
还是以房价为例,如果房价和面积,交通,学区三个因素有关,
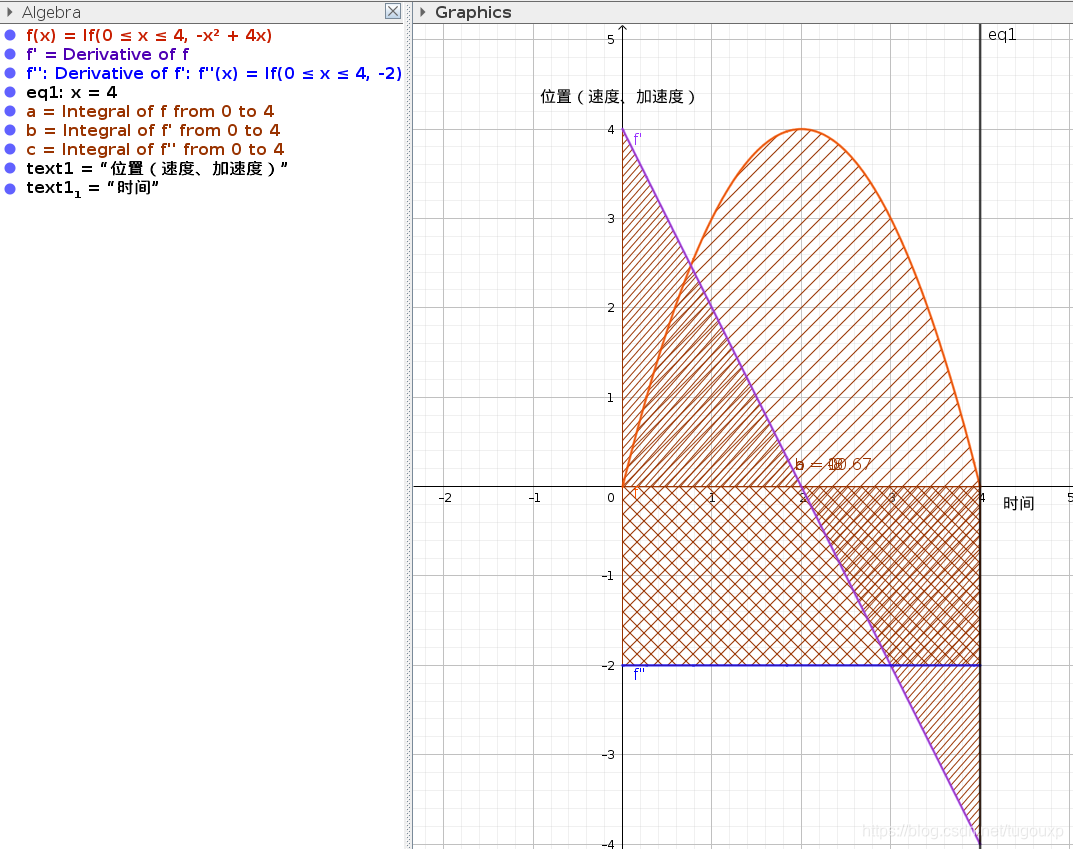
![]() , x代表面积,y代表交通,z标识学区。
, x代表面积,y代表交通,z标识学区。
可考虑先把交通和学区固定,考虑面积的微小变化对房价产生的影响,表示成:
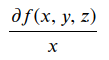
同理,分别再把面积和交通固定,以及面积和学区固定在某一个点,得到分别对于交通和学区的变化率.

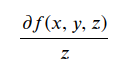
这种在多元函数中,将其他变量看做常数,按照求导法则,计算针对某个变量的导数,叫做偏导数.偏导数每次只使一个自变量发生变化,所以计算过程和计算一元函数的导数过程无异。
说到这里,实际上已经和梯度发生联系了, 实际上就代表了梯度.
实际上就代表了梯度.
比如函数:

求偏导的结果为:


梯度:
百度百科对梯度的定义,梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)
设圆锥的方程为:
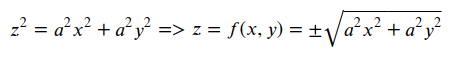
其中,a为变参,这里取a=2
则针对曲面上每一个点P(x,y), 其梯度可以定义为

其中
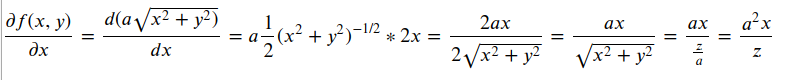
同理
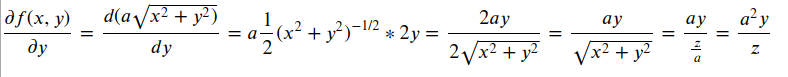
所以,在椎体的任意一点,梯度向量为

记做:

特殊情况下,在y=0截面和x=0截面与圆交线上的点的梯度为
![]()
如下图所示,由于梯度在另一个方向上的分量为0,所以梯度向量在坐标轴方向上达到最大,这和直觉是相符的。
直觉上,不论从圆锥上哪个点触发,它的梯度的大小是一样的(方向不一样),我们可以验证一下
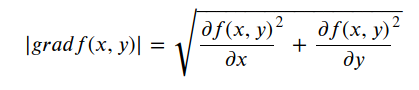
所以
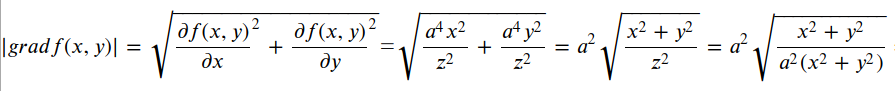
=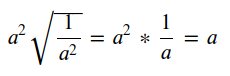
所以,圆锥上任意一点的梯度大小均为a,处处相等,包括上面计算得到的和坐标轴平面相交的两条线。
 叫做二维空间向量梯度算子,
叫做二维空间向量梯度算子,


下图中的v1向量即是梯度向量

还可以从方向导数的角度来解释梯度的概念,所谓方向导数,就是指函数f(x,y)沿着直线L变化的速率,这条直线其实就是曲面上相对应的那条曲线在xoy平面的投影,完成投影的这个竖立的平面就称为投影平面,那么,方向导数其实就是空间曲线沿着它自己在xoy平面的投影直线的变化率。正如dy/dx表示二维平面中一条曲线在某一点沿着x轴的变化速率(也就是切线的斜率)一样.
首先看一下方向导数的定义:

转换成如下的形式:

角theta是直线l和x轴的夹角.
那么,方向导数在L指向何方的时候取得最大值呢?
设
![]()
是方向L上的单位向量,
则方向导数可以写成:
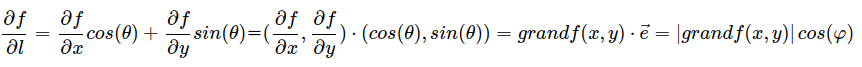
其中fai角是投影直线L和梯度的夹角,不难得出,当fai角为0时,方向导数取得最大值,换句话说,当方向导数和梯度同向时,变化率最大.
方向导数的最大值即是梯度:
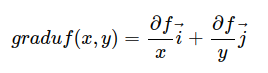
有另外一个概念和梯度的联系非常紧密,它就是等高线,对于三维空间曲面来说,等高线就是平行于XOY平面和曲面图形交线在xoy平面的投影,例如,下面图形显示的马鞍面的等高线,它的等高线每一组都是双曲线。

来个会动的:

当采用等高线的概念后,等高线和梯度有一个非常有趣的关系,实际上,等高线和梯度方向是互相垂直的,以三维曲面等高线为例,推导如下:
等高线方程为:
则,该曲线在xoy平面上的投影是一条曲线,在xoy平面上该曲线的方程为:
曲线上一点P的斜率,根据隐函数求导公式,两边对x求导:
而梯度向量定义为:
梯度方向斜率为:
所以,梯度方向和等高线切线方向垂直。
上面计算的圆锥面梯度处处相同,为a,这里a=2。对于以上方向导数,梯度向量,等高线,等高线法线的几何意义的说明,用一幅图结束本文:

点的投影在x轴上的情形:

结束!