所谓线性DP是,是指我们的递推方程是有着明显的线性关系的。动态规划中每个状态都是多维的状态,多维状态有一个求解的顺序,比如背包问题是一个二维的,求的时候一行一行的来求,这样的DP我们称之为线性DP。
数字三角形
问题描述
给定一个如下图所示的数字三角形,从顶部出发,在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输入格式
第一行包含整数n,表示数字三角形的层数。
接下来n行,每行包含若干整数,其中第 i 行表示数字三角形第 i 层包含的整数。
输出格式
输出一个整数,表示最大的路径数字和。
数据范围
1 ≤ n ≤ 500,
−10000 ≤ 三角形中的整数 ≤ 10000
输入样例:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出样例:
30
解题思路:
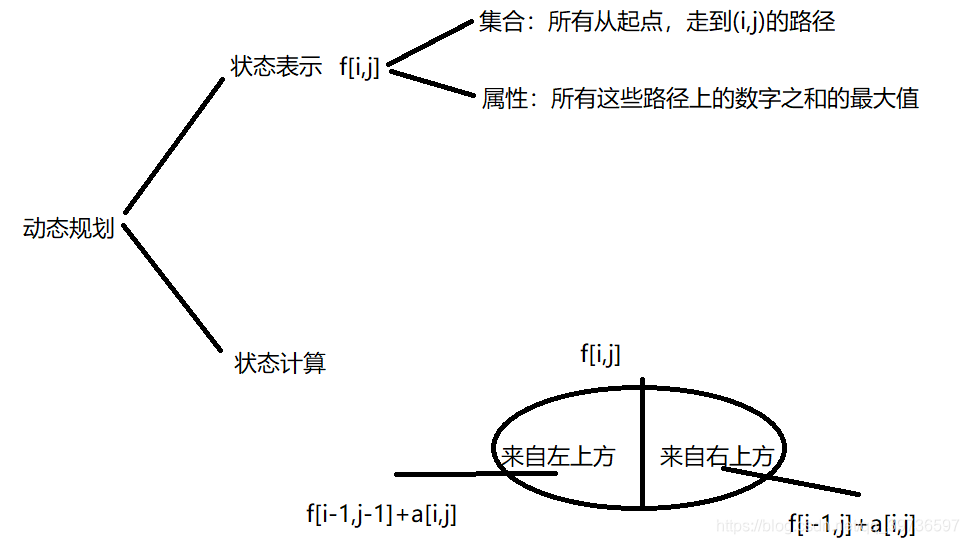
通过以上分析,我们得出,状态转移方程是来自左上方的最大值i-1,j-1和来自右上方的最大值i-1,j的两者最大值再加上该位置的值。
动态规划时间复杂度:状态的数量乘以转移的计算量,这里总共时间复杂度是O(n2)
这里我们是从下往上做,因此最开始的时候我们初始化边界问题。即最后一行的数字之和已经为该位置上的值。然后依次往上求,那么最后0,0位置上的值就是我们数字三角形的最大和。 如果是从上往下,那么最后一行的位置上还要考虑哪一个是最大值。显然从下往上遍历的话代码会更简洁一点。
#include<algorithm>
#include<iostream>
using namespace std;
#define N 1010
int n;
int tri[N][N];
int f[N];
int main(){
cin>>n;
//读入数字三角形
for(int i=0;i<n;i++){
for(int j=0;j<=i;j++){
cin>>tri[i][j];
}
}
//处理边界问题,注意,这里使用到了滚动数组
//我们从最后一行开始做
for(int i=0;i<n;i++){
f[i]=tri[n-1][i];
}
//状态转移方程
for(int i=n-2;i>=0;i--){
for(int j=0;j<=i;j++){
f[j]=tri[i][j]+max(f[j],f[j+1]);
}
}
cout<<f[0];
return 0;
}
最长上升子序列
问题描述
给定一个长度为N的数列,求数值严格单调递增的子序列的长度最长是多少。
输入格式
第一行包含整数N。
第二行包含N个整数,表示完整序列。
输出格式
输出一个整数,表示最大长度。
数据范围
1≤N≤1000,
−109≤数列中的数≤109
输入样例:
7
3 1 2 1 8 5 6
输出样例:
4
难度:简单
时/空限制:1s / 64MB
总通过数:9936
总尝试数:15166
解题思路:
3 1 2 1 8 5 6中的最长上升子序列为1256
状态表示这里的维度,我们要坚持一个原则,让答案能够推出来,在这个基础上,我们的维度越少越好,我们一般是从小到大的情况来考虑。
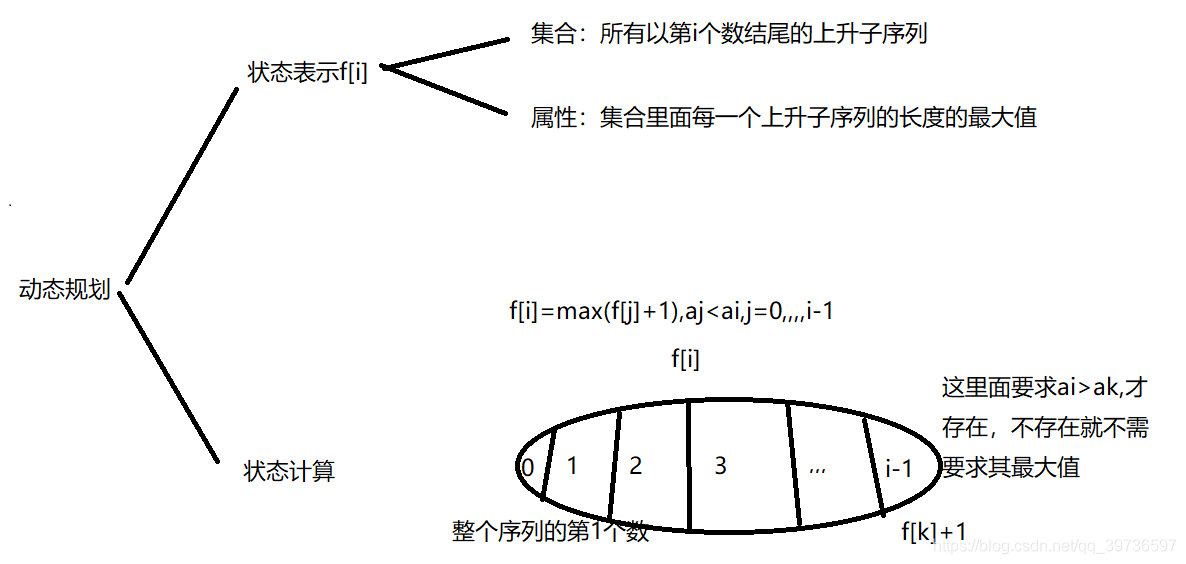
状态数量是O(N),转移的时间复杂度是O(N),所以时间复杂度是O(N2)
#include<iostream>
#include<algorithm>
using namespace std;
#define N 1010
int arr[N];
int n;
int maxLen[N];
int main(){
cin>>n;
//初始化最长上升子序列为1
for(int i=0;i<n;i++){
cin>>arr[i];
maxLen[i]=1; //只有a[i]一个数的情况
}
//从前往后处理每一个状态
for(int i=1;i<n;i++){
for(int j=i-1;j>=0;j--){
//只有aj<ai的时候,我们才计算最长上升子序列
if(arr[i]>arr[j]){
maxLen[i]=max(maxLen[i],maxLen[j]+1);
}
}
}
int res;
//最后选取一个最长上升子序列
for(int i=0;i<n;i++){
res=max(res,maxLen[i]);
}
cout<<res;
return 0;
}
最长公共子序列
问题描述
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列,则返回 0。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace",它的长度为 3。
示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc",它的长度为 3。
示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0。
解题思路
最长公共子序列(Longest Common Subsequence,简称 LCS)是一道非常经典的面试题目,因为它的解法是典型的二维动态规划,大部分比较困难的字符串问题都和这个问题一个套路,比如说编辑距离。而且,这个算法稍加改造就可以用于解决其他问题,所以说LCS算法是值得掌握的。
所谓子序列,就是要保留原始顺序,但可以是不连续的。审题之后你可能会有疑问,这个问题为啥就是动态规划来解决呢?因为子序列类型的问题,穷举出所有可能的结果都不容易,而动态规划算法做的就是穷举 + 剪枝,它俩天生一对儿。所以可以说只要涉及子序列问题,十有八九都需要动态规划来解决。
第一步,一定要明确 dp 数组的含义。
对于两个字符串的动态规划问题,套路是通用的。
比如说对于字符串 s1 和 s2,它们的长度分别是 m、n,一般来说都要构造一个这样的 DP table:int[][] dp = new int[m+1][n+1]。
这里为什么要加1,原因是你可以不加1,但是不加1你就会用其它限制条件来确保这个index是有效的,而当你加1之后你就不需要去判断只是让索引为0的行和列表示空串。
第二步,定义边界条件
我们专门让索引为0的行和列表示空串,dp[0][…] 和 dp[…][0] 都应该初始化为0,这就是base case。
第三步,找状态转移方程
这是动态规划最难的一步,我们来通过案例推导出来。
对于 text1:abcde 和 text2:ace 两个字符串,我们定义两个指针进行遍历 i 和 j。
遍历 text1 长度为 m,定义指针 i,从 0~m。固定 i 指针(i == 1)位置,接下来开始遍历 text2 长度为 n,定义指针 j,从 0~n。
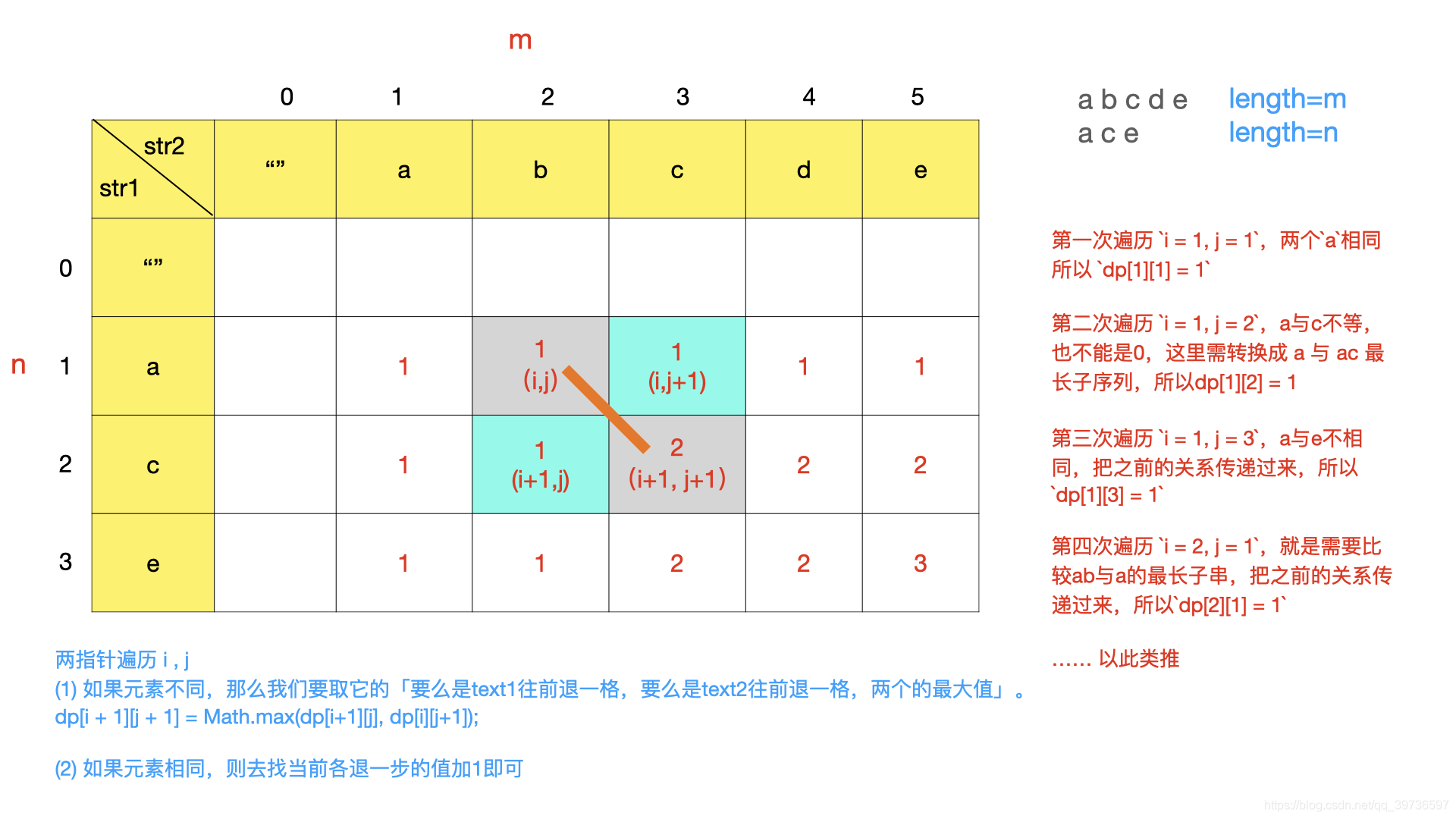
第一次遍历 i = 1, j = 1,两个a相同所以 dp[1][1] = 1
第二次遍历 i = 1, j = 2,a与c不等,也不能是0,这里需转换成 a 与 ac 最长子序列,这里需要把之前的关系传递过来,所以dp[1][2] = 1
第三次遍历 i = 1, j = 3,a与e不相同,把之前的关系传递过来,所以dp[1][3] = 1
text2:ace 已经走完来第一轮,接下来text1:abcde 走到来b字符。
第四次遍历 i = 2, j = 1,就是需要比较ab与a的最长子串,把之前的关系传递过来,所以dp[2][1] = 1
依次类推…(详看上图)
我们会发现遍历两个串字符,当不同时需要考虑两层遍历前面的值(关系传递),也就是左边和上边的其中较大的值,当想相同时,需要考虑各自不包含当前字符串的子序列长度,再加上1。
因此可以得出:
现在对比的这两个字符不相同的,那么我们要取它的「要么是text1往前退一格,要么是text2往前退一格,两个的最大值」
dp[i + 1][j + 1] = Math.max(dp[i+1][j], dp[i][j+1]);
对比的两个字符相同,去找它们前面各退一格的值加1即可:dp[i+1][j+1] = dp[i][j] + 1;
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int m=text1.length(),n=text2.length();
int [][] cs=new int[m+1][n+1];
//设置边界条件
for(int i=0;i<=m;i++){
cs[i][0]=0;
}
for(int i=0;i<=n;i++){
cs[0][i]=0;
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
//状态转移方程
if(text1.charAt(i-1)==text2.charAt(j-1)){
cs[i][j]=cs[i-1][j-1]+1;
}else{
cs[i][j]=Math.max(cs[i-1][j],cs[i][j-1]);
}
}
}
return cs[m][n];
}
}