jzoj6263. 【省选模拟8.5】可见的点

题目描述

Description

Input

Output

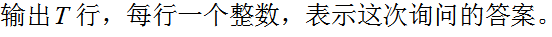
Sample Input
4
1
10
2
10 10
3
6 9 11
10
999 990 988 981 977 972 966 963 955 954

Sample Output
2
82
570
339367556

Data Constraint

Hint

70%

大力猜结论
斐波那契数列的性质：
①$gcd(F(n-1),F(n))=1$
②$F(n)=F(m+1)F(n-m)+F(m)F(n-m-1)$
③$gcd(F(n),F(m))=F(gcd(n,m)$
证明：
①
反证，若$gcd(F(n-1),F(n))=a$（a>1），那么a|F(n-1)、a|F(n)
因为F(n)=F(n-1)+F(n-2)，则a|F(n-2)
如此类推，发现a|F(1)
因为a>1且F(1)=1，所以不成立
②
归纳：已证得$F(n)=F(m)F(n-m+1)+F(m-1)F(n-m)$，边界为$F(n)=F(2)F(n-1)+F(1)F(n-2)$（m=1）
$F(n)=F(m)F(n-m+1)+F(m-1)F(n-m)$
$F(n)=F(m)F(n-m)+F(m)F(n-m-1)+F(m-1)F(n-m)$
$F(n)=(F(m)+F(m-1))F(n-m)+F(m)F(n-m-1)$
$F(n)=F(m+1)F(n-m)+F(m)F(n-m-1)$
③
$gcd(F(n),F(m))=gcd(F(m+1)F(n-m)+F(m)F(n-m-1),F(m))$
$gcd(F(n),F(m))=gcd((F(m+1)F(n-m)+F(m)F(n-m-1))modF(m),F(m))$
因为$gcd(a\ast b,c)=gcd(b,c)$（ac互质）且$gcd(F(m),F(m+1))=1$
$gcd(F(n),F(m))=gcd(F(n-m),F(m))$
可以发现上面的式子类似求gcd
因为$gcd(a,b)=gcd(gcd(a,b),0)$
类比可得$gcd(F(n),F(m))=gcd(F(gcd(n,m)),F(0))=F(gcd(n,m))$（F(0)=0）
（这个式子对多个数也是成立的）
参考：https://www.cnblogs.com/Milkor/p/4734763.html

---

终于扯完了
根据题意，一个点能被看到当且仅当gcd(F[i1],F[i2]…F[in])=1，即F[gcd(i1,i2,…in)]=1
显然gcd(i1,i2,…in)只可能为1或2
于是就变成了求gcd(i1,i2,…in)=1 or 2的方案数
$ans={\sum }_{d=1}^2{\sum }_{i1=1}^{a1}{\sum }_{i2=1}^{a2}...{\sum }_{in=1}^{an}[gcd(i1,i2,...,in)=d]$
显然直接反演+暴力算就有70了

100%

对70%的式子整数分块，一共只需要跳O(n√m)次，时间复杂度为O(Tn√m)

code

#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define min(a,b) (a<b?a:b)
#define mod 1000000009
#define Mod 1000000007
#define Len 1000000
using namespace std;

int p[Len+1];
bool F[Len+1];
int a[1000001];
int miu[1000001];
int Miu[1000001];
int T,n,i,j,k,l,len,ls;
long long ans,s,mn,Ans;

void init()
{
    
    
	miu[1]=1;
	
	fo(i,2,Len)
	{
    
    
		if (!F[i])
		{
    
    
			miu[i]=-1;
			p[++len]=i;
		}
		
		fo(j,1,len)
		if ((long long)i*p[j]<=Len)
		{
    
    
			F[i*p[j]]=1;
			miu[i*p[j]]=-miu[i];
			
			if (!(i%p[j]))
			{
    
    
				miu[i*p[j]]=0;
				break;
			}
		}
		else
		break;
	}
	
	fo(i,1,Len)
	Miu[i]=Miu[i-1]+miu[i];
}

long long f()
{
    
    
	int Min;
	
	ans=0;
	ls=1;
	
	while (ls<=mn)
	{
    
    
		Min=233333333;
		
		s=1;
		fo(j,1,n)
		{
    
    
			Min=min(Min,a[j]/(a[j]/ls));
			s=s*(a[j]/ls)%mod;
		}
		
		Min=min(Min,mn);
		
		ans=(ans+s*(Miu[Min]-Miu[ls-1]))%mod;
		ls=Min+1;
	}
	
	return ans;
}

int main()
{
    
    
	freopen("point.in","r",stdin);
	freopen("point.out","w",stdout);
	
	init();
	
	scanf("%d",&T);
	for (;T;--T)
	{
    
    
		scanf("%d",&n);
		mn=233333333;
		
		fo(i,1,n)
		{
    
    
			scanf("%d",&a[i]);
			mn=min(mn,a[i]);
		}
		
		Ans=f();
		mn/=2;
		fo(i,1,n)
		a[i]/=2;
		
		printf("%lld\n",((Ans+f())%mod+mod)%mod);
	}
}