文章目录
章节2 结构归纳法
上一章定义的r关系是一个函数,但我们如何证明?这里有一个半正式的证明:
r关系由一对约束定义。第一个约束为以 f 开头的•表达式,结果由表达式的右侧部分唯一确定。第二个约束为以 f 开头的•表达式,结果被唯一确定为 t 。因为一个表达式仅可以以f或者t开头,所以只有一个约束会被应用,因此结果也是唯一的。
上述的论点是相当有说服力的,因为它以来于一个表达式直接可观察的性质:这个表达式由 f 还是 t 开头。其他关于 B 的关系可能不那么容易证明。例如,我们并不显而易见地发现 evalr 是一个函数。其根本原因是因为B是递归定义的,并没有能够直接列举所有有趣的案例的方法。所以,为了证明更加一般的论点,我们必须使用 归纳法 。
数学归纳法是以自然数为基础的。通常的证明过程为:
- 证明当 n = 0(1) 时成立。
- 假设 n = m 时成立,那么可以推导出在 n = m + 1 时论点也成立。
在大多数情况下,在我们将要考虑的证明中,并没有为集合元素提供肉眼可见的自然数 n,但是在论证一个表达式属于某个集合的过程中,可以基于论证的步骤数为表达式派生出我们所需要的自然数 n。
抛开为数学归纳法反复寻找合适的自然数的过程,我们将会使用 结构归纳法 ,它直接作用于语法定义的集合元素,其基本原理与数学归纳法一致。
2.1 结构归纳法的要素
结构归纳法应用在证明一个没有递归定义的集合时。只有在定义中由原子元素时,集合才是充分定义的。这些元素构成归纳证明的基本要素。 而定义中的自指(递归)元素则是归纳要素。
举例来说,我们有如下定义:
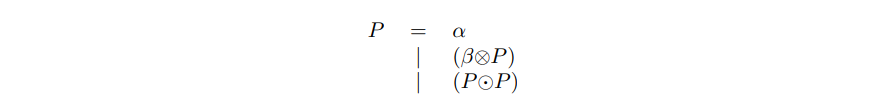
定义中 P 的成员包括 α, (β ⊗ α), (α O・ α) 和 ((β ⊗ (β ⊗ α)) O・ (β ⊗ α))。有关P的元素,现在有一个论证为:
定理 2.1: 对于任意P, P包含相等数量的 β 和 ⊗
这个定理的真假很明显。但由于定理2.1做了有关P所有可能的断言,并且P是递归定义的,所以它必须用结构归纳法所证明。
指南: 如果一个论点包含了一个递归定义集合的所有元素,则需要用到结构归纳法。
一个正确构造的归纳证明的关键是它能保证覆盖整个集合。例如上述的P集合,这里有一个例子来例证定理2.1
定理 2.1 的一个证明:
-
基本要素:
-
要素α
α 包含 0 个 β 以及 0 个 ⊗,所以论证成立
-
-
归纳要素:
-
要素 (β⊗P)
在递归中,由于 P 是 (β⊗P) 的子结构,P 包含了相同数量(n)的 β 和 ⊗。因此,(β⊗P) 包含n+1个 β 和 ⊗,论证仍然成立
-
要素 (P1 O・ P2)
在递归中, P1包含了相同数量(n1)的 β 和 ⊗,P2同样包含了相同数量(n2)的 β 和 ⊗,因此,P1 O・ P2 包含了n1+n2个 β 和 ⊗,论证仍然成立
-
上述的证明拥有一个规范的形式。 在导言中,“通过归纳P的结构” 封装了一个样板论证,其运行方式如下:
- 论证必须对于任意P成立。因此,假设提供了一个任意的P元素。如果P具有基本要素(即其中没有自指),我们证明如何根据基本要素立即推断论证。如果P为归纳要素(有自指),则依赖归纳法,假设P中子结构的论证成立,然后推导出论证。根据结构归纳法的原理,该论证适用于任意的P(即论证成立)。
定理2.1的证明中包含了单个基本要素,因为P的定义中只包含了一个基本要素。证明包含了两个归纳要素,因为P的定义中包含了两个自指定义。
指南:对于一个结构归纳证明的标准格式,基本要素部分应为集合定义中的每一个基本要素都提供证明。同样,归纳要素部分,应为集合定义中的每一个归纳要素都提供证明。
结构归纳证明的标准格式对证明者和阅读者都起着指导作用。证明者为各个要素逐一展开论证,而阅读者则可以快速检查整个证明过程是否标准,并且可以集中精力分别检查每个要素证明的正确性。
有时,在基本要素或者归纳要素部分中,分割要素使用的是结构归纳法以外的标准,这种分割方法仅仅区分深层嵌套的要素,因此是可以接受的。一个不标准的要素分割必须以明显的方式囊括所有的要素。
所有证明(包括定理 2.1)都有如下的格式:

证明中的细节决定于论证。下述的论证也是囊括所有P元素,因此具有上述相同的格式。
定理 2.2 对于任意P,P包含至少一个 α
练习 2.2
证明定理 2.2
题解
证明如下
-
基本要素:
-
要素α
α 包含 1 个 α,论证成立
-
-
归纳要素:
-
要素 (β⊗P)
在递归中,P 包含至少一个 α,因此 (β⊗P) 包含至少一个 α,论证仍然成立
-
要素 (P1 O・ P2)
在递归中, P1 包含至少一个 α, P2 也包含至少一个 α,论证仍然成立
-
证毕。