先放一下代码。因为是照着黑皮书《数据结构与算法分析》学的,所以代码大致和书上的一样,我并没有做太多修改。只是在理解原理的时候有些比较棘手的地方,所以在这里记笔记,方便以后查看。
int max(int n1,int n2)
{
if (n1 >= n2)
return n1;
else
return n2;
}
//取最大值
static int Height(position P)
{
if (P = NULL)
return -1;
else
return P->height;
}
//获取高度//只是通过结构内定义的高度去取值,没有测算
static position SingleRotateWithLeft(position K2)
{
position K1;
K1 = K2->left;
K2->left = K1->right;
K1->right = K2;
K1->height = max(Height(K1->left), Height(K1->right)) + 1;
K2->height = max(Height(K2->left), Height(K2->right)) + 1;
return K1;
}
//单旋转(左树旋转)
static position DoubleRotateWithLeft(position K3)
{
K3->left = SingleRotateWithRight(K3->left);
return SingleRotateWithLeft(K3);
}
//双旋转(左树旋转)
static position SingleRotateWithRight(position K1)
{
position K2;
K2 = K1->right;
K1->right = K2->left;
K2->left = K1;
K1->height = max(Height(K1->left), Height(K1->right)) + 1;
K2->height = max(Height(K2->left), Height(K2->right)) + 1;
return K2;
}
//单旋转(右树旋转)
static position DoubleRotateWithRight(position K3)
{
K3->right = SingleRotateWithLeft(K3->right);
return SingleRotateWithRight(K3);
}
//双旋转(右树旋转)
avltree insert(int X,avltree T)
{
if (T == NULL)
{
//T为空节点
T = new avlnode;//假定空间永远是足够的
T->height = 0;
T->left = T->right = NULL;
T->info = X;
}
if (X < T->info)
{
T->left = insert(X, T->left);
if (Height(T->left) - Height(T->right) >= 2)//事实上等于2才是最合适的
{
if (X < (T->left->info))
T = SingleRotateWithLeft(T);
else
T = DoubleRotateWithLeft(T);
}
}
else if (X > T->info)
{
T->right = insert(X, T->right);
if (Height(T->right) - Height(T->left) >= 2)//事实上等于2才是最合适的
{
if (X > (T->right->info))
T = SingleRotateWithRight(T);
else
T = DoubleRotateWithRight(T);
}
}
T->height = max(Height(T->left), Height(T->right)) + 1;
return T;
}
如果你也有这本书,并且已经看过这一部分关于avl的描述了,那么关于“什么是avl树”以及这些代码的作用至少是明白的,这里我主要是对书中所写的insert函数做些笔记。
因为在树这一节中,很多地方都是通过递归来实现的,不得不承认这是一种非常巧妙的方法,但对于我这种小白来说,阅读和分析递归代码往往会转不过弯(其实更多时候是我懒得动笔,只在脑子里转了几十个循环,最后把自己绕懵了......)
写在前面,书中的element我用int类型的info代替了,我觉得这样会更容易理解(虽然这样做其实也没什么意义就是了)。
-------------------------------------------------------------------------------
Insert过程分析:
首先,这段函数的第一部分用来判断T节点是否存在。但我最开始还在奇怪,因为我们通常都是创建好了一颗空树,然后再进行插入节点的工作,而这里却要判断T节点是否为空。
但可能是书上对这里的解释并不是那么清楚,这里我说一些自己的看法,如果有问题,欢迎指出。
函数中的X代表的就是info,而T则应该输入我们要进行操作的树的根节点地址,毕竟我们也不清楚这个X应该放到树的什么地方。
但值得注意的是,我们是在使用递归来实现这个功能,也就是说,在每一次递归循环中,T节点是不断改变的,它最终会找到我们要插入数据的实际位置,并在这个地方开辟出新的节点,这才是这段函数的作用。
那么关键其实就在于寻址了。找到X应该放置的位置其实并不难,ADT树中也已经说过这种方法,但找到之后,却要按照AVL树的性质来存放数据。
假设,我们通过函数递归,T参数已经来到了NULL的位置,于是这一次的递归中第一次开辟出了新节点。于是我们将新节点的地址返回到了上一次递归中(显然X=T->info,所以其他判断都不起作用了)。
不妨假设我们上一次是向左树去找,大概就是下面这样(没用鼠标垫,所以漂移的有点厉害......):
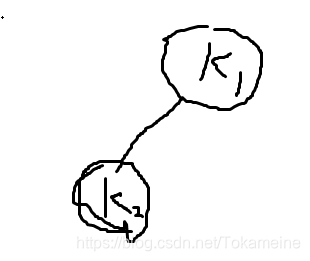
所以这一次,T节点实际上是指K1。
T->left = insert(X, T->left);
而我们刚执行完这条函数,接下来判断K1节点是否打破了平衡状态。
if (Height(T->left) - Height(T->right) >= 2)//事实上等于2才是最合适的
(之所以会有这道注释,其实只是我的喜好罢了。因为如果在创建和修改二叉树的时候都有这样的操作,那么左树和右树的高度差值根本不可能超过2,因为一旦达到2就会被重新平衡,但我还是想这样写.....)
假设我们这一次没有打破这个平衡,那么最终我们将会返回K1的地址。
注:这里有个巧妙的地方,
T->height = max(Height(T->left), Height(T->right)) + 1;
这段函数能够保证每一次插入节点的时候,都能为它获取高度。假设现在有一颗空树,我插入的第一个节点T1就获得了高度‘0’,而再次插入新节点T2的时候,T2的高度是‘0’,而这条代码获取了T2的高度又+1,变成了自己的高度,从而到达了高度‘1’。如果每个节点都通过这个函数来插入,那么深度自然就被设定好了。
------------------------------------------------------------------------------------
假设我们从上一次递归出来,回到了下图这个位置。本次递归中T代表了K3的地址。
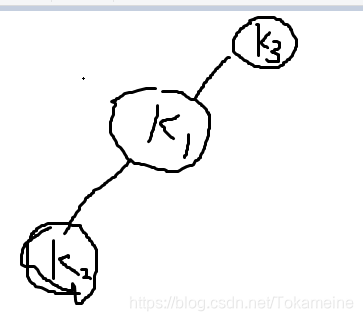
现在,我们通过判断,发现K3打破了平衡状态,于是做了一个奇怪的判断:
if (X < (T->left->info))
函数在判断X是不是小于K1的关键值。
如果判断为真,其实就说明K2会成为K1的左节点,那么就要进行左树单旋转操作。
如果判断为假,说明K2是K1的右节点,那么就要进行左树的双旋转操作。
(判断左树还是右树,其实是根据K1的位置判断。很简单,所以不再赘述)
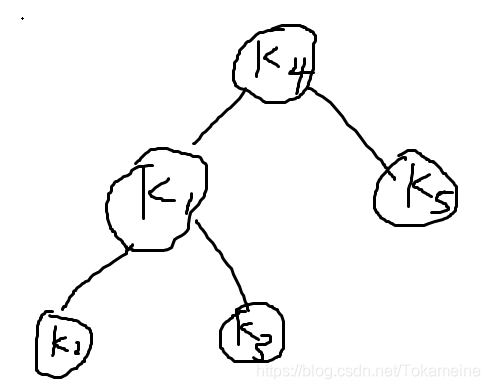
旋转结束之后,返回了K1的地址(这个地址怎么来的,写在左树单旋转函数里了,该函数返回新根)。
假设这一次是平衡的,那么大概会长上图这样了。
最后就是把剩下的还没走完的递归流程走完就行了,这个过程中通常不会再有什么操作了,因为如果你每一次放入节点都用这个函数来操作,基本上都能保证当前的树是一颗正常的树,放入的新节点最多只能影响到它的‘祖父母辈’的平衡状态,只要把‘祖父母辈’的平衡修正回来,通常整棵树都会平衡。
(这个结论是我自己猜测的,如果有错误欢迎指出)