一、对阶

类比平常我们用到的带阶数的加减法，我们常常会把两个数的阶数转化为一致，再针对尾数进行加减法运算，计算机中也是一样。

对以上两个浮点数，我们进行对阶，首先求他们的阶差

在对阶的过程中有两种方式，大阶向小阶看齐，小阶向大阶看齐。

但是在计算机中，因为存储空间的字长限制，如果我们使用大阶向小阶看齐，需要把数字向左移，可能把数字的最高位给移除掉，从而使整个数据出现错误；

如果我们使用小阶向大阶看齐，需要把数字向右移，有可能丢失数据的精度，但不会使整个数据出现错误；

因此我们对阶的原则是

小阶向大阶看齐

，求 X + Y

二、规格化

1、规格化的判断

判断一个数是否是规格化数，计算机中可以通过亦或电路，比较一个数补码的符号位跟第一位数是否相同来实现。

例如：

例如：S = -1

2、如何进行规格化

详细规格化操作请参照我的另一篇文章：计算机组成原理12-数的定点表示和浮点表示

规格化分为左归和右归

（1）左归

尾数左移一位（大小变为原来的两倍），阶码减 1 ，直到数符和第一数位不同为止

，计算 X + Y的结果为： [ x + y ] 补 = 00, 11; 11. 1001 ，

结果为非规格化数，左归后

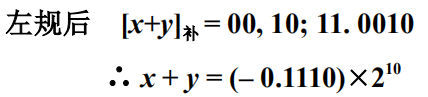
（2）右归

当尾数溢出（ >1 ）时，需右规，即尾数出现 01. ××…×或 10. ××…×时，尾数右移一位，阶码加 1

总结：

①两个符号位不相同，右规：两个符号位不同，说明运算结果溢出。此时要进行右规，即把运算结果的尾数右移一位。

需要右规的只有如下两种情况：01××××和10××××。01×××右移一位的结果为001×××；10××××右移一位的结果为110×××。最后将阶码（指数）+1。

②两个符号位相同，但是最高数值位与符号位相同，左规：两个符号位相同，说明没有溢出。此时要把尾数连续左移，直到最高数值位与符号位的数值不同为止。

需要左规的有如下两种情况：111×××和000×××。111×××左移一位的结果为11×××0；000×××左移一位的结果为00×××0。最后将阶码（指数）减去移动的次数。

例如：

通过双符号位，我们可以知道尾数相加后，尾数溢出，因此我们需要进行右归

三、舍入

执行右规或者对阶时，有可能会在尾数低位上增加一些值，最后需要把它们移掉。（进行尾数加减时不要把对阶过程在尾数低位上增加的值去掉，不是不去掉，而是在舍入这一步去掉。）比如说，原来参与运算的两个数（加数和被加数）算上符号位一共有6个数，通过一系列操作后运算结果变成了8个数，这时需要把第7和8位的数去掉。如果直接去掉，会使精度受影响，通常有下边两个方法：

（1）0舍1入法

比如：X = 00.11010111，假设原本加数和被加数算上符号位一共有6个数，结果X是10个数，那么要去掉后四个数（0111）。由于0111首位是0（即要去掉的数的最高位为0），这种情况下，直接去掉这四个数就可以。所以最后结果为 X = 00.1101
结果 X = 00.11001001，这时要去掉的数为1001四个数，由于这四个数的首位为1（即要去掉的数的最高位为1），这种情况下，直接去掉这四个数，再在去掉这四个数的新尾数的末尾加1。如果+1后又出现了溢出，继续进行右规操作。所以最后结果为 X = 00.1101。