《百面机器学习》读书笔记（七）-优化算法

全部笔记的汇总贴：《百面机器学习》-读书笔记汇总

优化是应用数学的一个分支，也是机器学习的核心组成部分。实际上，机器学习算法 = 模型表征 + 模型评估 + 优化算法。其中，优化算法所做的事情就是在模型表征空间中找到模型评估指标最好的模型。不同的优化算法对应的模型表征和评估指标不尽相同，比如经典的支持向量机对应的模型表征和评估指标分别为线性分类模型和最大间隔，逻辑回归对应的模型表征和评估指标则分别为线性分类模型和交叉熵。

随着大数据和深度学习的迅猛发展，在实际应用中面临的大多是大规模、高度非凸的优化问题，这给传统的基于全量数据、凸优化（这里有一门凸优化的课程，时间充足的话，可以了解一下：中科大_凸优化）的优化理论带来了巨大的挑战。如何设计适用于新场景的、高效的、准确的优化算法成为近年来的研究热点。优化虽然是一门古老的学科，但是大部分能够用于训练深度神经网络的优化算法都是近几年才被提出，如Adam算法等。

虽然，目前大部分机器学习的工具已经内置了常用的优化算法，实际应用时只需要一行代码即可完成调用。但是，鉴于优化算法在机器学习中的重要作用，了解优化算法的原理也很有必要。

一、有监督学习的损失函数

机器学习算法的关键一环是模型评估，而损失函数定义了模型的评估指标。可以说，没有损失函数就无法求解模型参数。不同的损失函数优化难度不同，最终得到的模型参数也不同，针对具体的问题需要选取合适的损失函数。

• ★☆☆☆☆ 有监督学习涉及的损失函数有哪些？请列举并简述它们的特点。

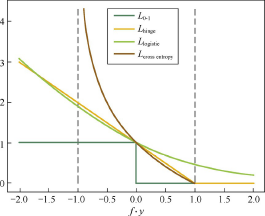
• 0-1损失$$L_{0-1}(f,y)=1_{fy\le 0}$$其中$1_P$是指示函数（Indicator Function），当且仅当$P$为真时取值为1，否则取值为0。该损失函数能够直观地刻画分类的错误率，但是由于其非凸、非光滑的特点，使得算法很难直接对该函数进行优化。
• Hinge损失函数(0-1损失的一个代理损失函数) L h i n g e ( f , y ) = max ⁡ { 0 , 1 − f y } L_{hinge}(f,y)=\max\{0,1-fy\} Lhinge​(f,y)=max{ 0,1−fy}Hinge损失函数是0-1损失函数相对紧的凸上界，且当$fy\ge 1$时，该函数不对其做任何惩罚。Hinge损失在$fy=1$处不可导，因此不能用梯度下降法进行优化，而是用次梯度下降法（Subgradient Descent Method）。
• Logistic损失函数(0-1损失的另一个代理损失函数)$$L_{logistic}(f,y)={\log }_2(1+\exp (-fy))$$Logistic损失函数也是0-1损失函数的凸上界，且该函数处处光滑，因此可以用梯度下降法进行优化。但是，该损失函数对所有的样本点都有所惩罚，因此对异常值相对更敏感一些。
• 交叉熵损失函数(当预测值$f\in [-1,1]$时0-1损失的代理损失函数)$$L_{crossentropy}(f,y)=-{\log }_2(\frac{1+fy}{2})$$交叉熵损失函数也是0-1损失函数的光滑凸上界。

四种损失函数的图像如下图所示。

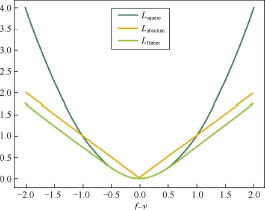
• 对于回归问题，常用平方损失函数$$L_{square}(f,y)=(f-y{)}^2$$平方损失函数是光滑函数，能够用梯度下降法进行优化。然而，当预测值距离真实值越远时，平方损失函数的惩罚力度越大，因此它对异常点比较敏感。
• 绝对损失函数(为解决上述问题)$$L_{absolutc}(f,y)=|f-y|$$绝对损失函数相当于是在做中值回归，相比做均值回归的平方损失函数，绝对损失函数对异常点更鲁棒一些。但是，绝对损失函数在$f=y$处无法求导数。
• Huber损失函数(综合考虑可导性和对异常点的鲁棒性)$$L_{Huber}(f,y)=\{\begin{array}{l}(f-y{)}^2,|f-y|\le \delta \\ \\ 2\delta |f-y|-{\delta }^2,|f-y|>\delta \end{array}$$Huber损失函数在$|f-y|$较小时为平方损失，在$|f-y|$较大时为线性损失，处处可导，且对异常点鲁棒。

上述三种损失函数的曲线如下图所示。

二、机器学习中的优化问题

大部分机器学习模型的参数估计问题都可以写成优化问题。机器学习模型不同，损失函数不同，对应的优化问题也各不相同。了解优化问题的形式和特点，能帮助我们更有效地求解问题，得到模型参数，从而达到学习的目的。

• ★★☆☆☆ 机器学习中的优化问题，哪些是凸优化问题，哪些是非凸优化问题？请各举一个例子。

逻辑回归，对应的优化问题就是凸优化问题。
主成分分析对应的优化问题是非凸优化问题。
其他凸优化问题的例子包括支持向量机、线性回归等线性模型，非凸优化问题的例子包括低秩模型（如矩阵分解）、深度神经网络模型等。
关于凸优化，还是再推荐一下中科大的这个课：中科大_凸优化

三、经典优化算法

• ★★☆☆☆ 无约束优化问题的优化方法有哪些？

经典的优化算法可以分为直接法和迭代法两大类。

• 直接法，顾名思义，就是能够直接给出优化问题最优解的方法。需满足两个条件，目标函数是凸函数，目标函数在$\theta$处有闭式解。（岭回归）
• 迭代法就是迭代地修正对最优解的估计。（直接法要满足的这两个条件限制了它的应用范围。因此，在很多实际问题中，会采用迭代法。）（牛顿法、梯度下降法）

四、梯度验证

在用梯度下降法求解优化问题时，最重要的操作就是计算目标函数的梯度。对于一些比较复杂的机器学习模型，如深度神经网络，目标函数的梯度公式也非常复杂，很容易写错。因此，在实际应用中，写出计算梯度的代码之后，通常需要验证自己写的代码是否正确。

• ★★☆☆☆ 如何验证求目标函数梯度功能的正确性？

五、随机梯度下降法

经典的优化方法，如梯度下降法，在每次迭代时需要使用所有的训练数据，这给求解大规模数据的优化问题带来了挑战。如何克服这个挑战，对于掌握机器学习，尤其是深度学习至关重要。

• ★☆☆☆☆ 当训练数据量特别大时，经典的梯度下降法存在什么问题，需要做如何改进？

随机梯度下降法用单个训练数据即可对模型参数进行一次更新，大大加快了收敛速率。
为了降低随机梯度的方差，从而使得迭代算法更加稳定，也为了充分利用高度优化的矩阵运算操作，在实际应用中我们会同时处理若干训练数据，该方法被称为小批量梯度下降法（Mini-Batch Gradient Descent）。
对于小批量梯度下降法的使用，有以下三点需要注意的地方。

• 如何选取参数m？在不同的应用中，最优的m通常会不一样，需要通过调参选取。一般m取2的幂次时能充分利用矩阵运算操作，所以可以在2的幂次中挑选最优的取值，例如32、64、128、256等。
• 如何挑选m个训练数据？为了避免数据的特定顺序给算法收敛带来的影响，一般会在每次遍历训练数据之前，先对所有的数据进行随机排序，然后在每次迭代时按顺序挑选m个训练数据直至遍历完所有的数据。
• 如何选取学习速率$\alpha$？为了加快收敛速率，同时提高求解精度，通常会采用衰减学习速率的方案：一开始算法采用较大的学习速率，当误差曲线进入平台期后，减小学习速率做更精细的调整。最优的学习速率方案也通常需要调参才能得到。

综上，通常采用小批量梯度下降法解决训练数据量过大的问题。每次更新模型参数时，只需要处理$m$个训练数据即可，其中$m$是一个远小于总数据量$M$的常数，这样能够大大加快训练过程。

六、随机梯度下降法的加速

• ★★☆☆☆ 随机梯度下降法失效的原因 —— 摸着石头下山。

为了获取准确的梯度，批量梯度下降法的每一步都把整个训练集载入进来进行计算，时间花费和内存开销都非常大，无法应用于大数据集、大模型的场景。相反，随机梯度下降法则放弃了对梯度准确性的追求，每步仅仅随机采样一个（或少量）样本来估计当前梯度，计算速度快，内存开销小。但由于每步接受的信息量有限，随机梯度下降法对梯度的估计常常出现偏差，造成目标函数曲线收敛得很不稳定，伴有剧烈波动，有时甚至出现不收敛的情况。
进一步地，有人会说深度学习中的优化问题本身就很难，有太多局部最优点的陷阱。没错，这些陷阱对随机梯度下降法和批量梯度下降法都是普遍存在的。但对随机梯度下降法来说，可怕的不是局部最优点，而是山谷和鞍点两类地形。山谷顾名思义就是狭长的山间小道，左右两边是峭壁；鞍点的形状像是一个马鞍，一个方向上两头翘，另一个方向上两头垂，而中心区域是一片近乎水平的平地。为什么随机梯度下降法最害怕遇上这两类地形呢？在山谷中，准确的梯度方向是沿山道向下，稍有偏离就会撞向山壁，而粗糙的梯度估计使得它在两山壁间来回反弹震荡，不能沿山道方向迅速下降，导致收敛不稳定和收敛速度慢。在鞍点处，随机梯度下降法会走入一片平坦之地（此时离最低点还很远，故也称plateau）。想象一下蒙着双眼只凭借脚底感觉坡度，如果坡度很明显，那么基本能估计出下山的大致方向；如果坡度不明显，则很可能走错方向。同样，在梯度近乎为零的区域，随机梯度下降法无法准确察觉出梯度的微小变化，结果就停滞下来。

• ★★★☆☆ 解决之道——惯性保持和环境感知。

随机梯度下降法本质上是采用迭代方式更新参数，每次迭代在当前位置的基础上，沿着某一方向迈一小步抵达下一位置，然后在下一位置重复上述步骤。

• 动量（Momentum）方法
  为了解决随机梯度下降法山谷震荡和鞍点停滞的问题，我们做一个简单的思维实验。想象一下纸团在山谷和鞍点处的运动轨迹，在山谷中纸团受重力作用沿山道滚下，两边是不规则的山壁，纸团不可避免地撞在山壁，由于质量小受山壁弹力的干扰大，从一侧山壁反弹回来撞向另一侧山壁，结果来回震荡地滚下；如果当纸团来到鞍点的一片平坦之地时，还是由于质量小，速度很快减为零。纸团的情况和随机梯度下降法遇到的问题简直如出一辙。直观地，如果换成一个铁球，当沿山谷滚下时，不容易受到途中旁力的干扰，轨迹会更稳更直；当来到鞍点中心处，在惯性作用下继续前行，从而有机会冲出这片平坦的陷阱。
• AdaGrad方法
  随机梯度下降法对环境的感知是指在参数空间中，根据不同参数的一些经验性判断，自适应地确定参数的学习速率，不同参数的更新步幅是不同的。例如，在文本处理中训练词嵌入模型的参数时，有的词或词组频繁出现，有的词或词组则极少出现。数据的稀疏性导致相应参数的梯度的稀疏性，不频繁出现的词或词组的参数的梯度在大多数情况下为零，从而这些参数被更新的频率很低。在应用中，我们希望更新频率低的参数可以拥有较大的更新步幅，而更新频率高的参数的步幅可以减小。AdaGrad方法采用“历史梯度平方和”来衡量不同参数的梯度的稀疏性，取值越小表明越稀疏。
• Adam方法
  Adam方法将惯性保持和环境感知这两个优点集于一身。一方面，Adam记录梯度的一阶矩（first moment），即过往梯度与当前梯度的平均，这体现了惯性保持；另一方面，Adam还记录梯度的二阶矩（second moment），即过往梯度平方与当前梯度平方的平均，这类似AdaGrad方法，体现了环境感知能力，为不同参数产生自适应的学习速率。一阶矩和二阶矩采用类似于滑动窗口内求平均的思想进行融合，即当前梯度和近一段时间内梯度的平均值，时间久远的梯度对当前平均值的贡献呈指数衰减。

除了上述三种随机梯度下降法变种，研究者还提出了以下几种方法。

• Nesterov Accelerated Gradient。该方法扩展了动量方法，顺着惯性方向，计算未来可能位置处的梯度而非当前位置的梯度，这个“提前量”的设计让算法有了对前方环境预判的能力。
• AdaDelta和RMSProp。这两个方法非常类似，是对AdaGrad方法的改进。AdaGrad方法采用所有历史梯度平方和的平方根做分母，分母随时间单调递增，产生的自适应学习速率随时间衰减的速度过于激进。针对这个问题，AdaDelta和RMSProp采用指数衰退平均的计算方法，用过往梯度的均值代替它们的求和。
• AdaMax。该方法是基于Adam方法的一个变种方法，对梯度平方的处理由指数衰退平均改为指数衰退求最大值。
• Nadam。该方法可看成Nesterov Accelerated Gradient版的Adam。

七、$L_1$正则化与稀疏性

为什么希望模型参数具有稀疏性呢？稀疏性，说白了就是模型的很多参数是0。这相当于对模型进行了一次特征选择，只留下一些比较重要的特征，提高模型的泛化能力，降低过拟合的可能。

• ★★★☆☆ $L_1$正则化使得模型参数具有稀疏性的原理是什么？

$L_1$正则化相当于为参数定义了一个棱形的解空间（$L_2$正则化类似于一个圆形的解空间）。如果原问题目标函数的最优解不是恰好落在解空间内，那么约束条件下的最优解一定是在解空间的边界上，而$L_1$“棱角分明”的解空间显然更容易与目标函数等高线在角点碰撞，从而产生稀疏解。
   \;
这是从解空间的形状出发，当然还可以从函数叠加和贝叶斯先验的角度出发来思考这个问题。

下一章传送门：《百面机器学习》读书笔记（八）-采样