跟着闫令琪老师的课程学习,总结自己学习到的知识点
课程网址GAMES101
B站课程地址GAMES101
课程资料百度网盘【提取码:0000】
计算机图形学概述
计算机图形学是一门将模型转化到屏幕上图像的一门基础学科,主要分为:Rasterization(光栅化)、Curves and Meshes(几何表示)、Ray Trancing(光线追踪)、Animation/Simulation(动画和模拟)
图形学与计算机视觉的简单界限:
(1) 计算机视觉是将屏幕上的图片转化为模型的过程;
(2) 计算机图形学是一门将模型转化到屏幕上图像的一门基础学科。
每个类别的知识框架如下图:
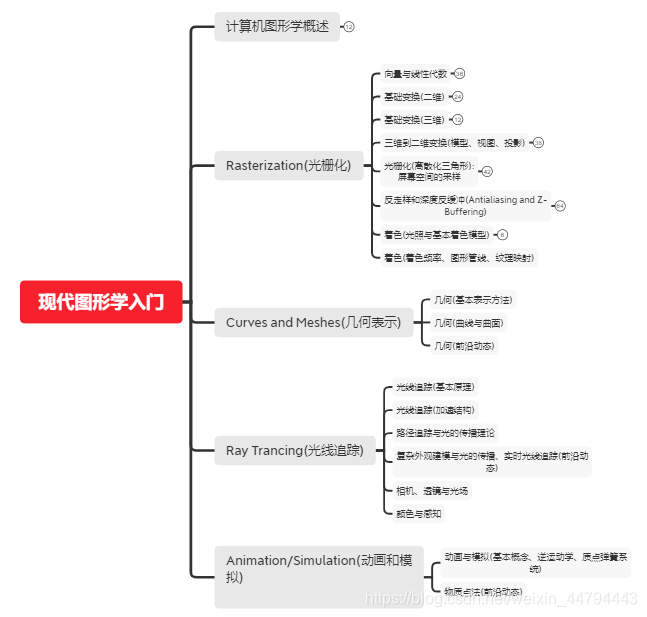
Rasterization(光栅化)
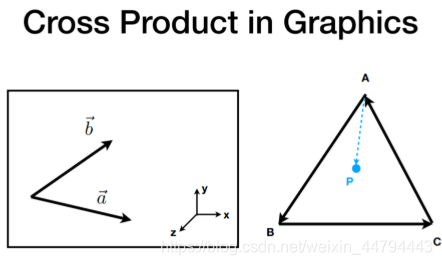
点乘和叉乘
Dot Multiplication
点乘在图形学的应用
(1) 求两个向量之间的夹角:
cos ( θ ) = ( a ⃗ ⋅ b ⃗ ) ∥ a ∥ ∥ b ∥ \cos(\theta) = \frac{(\vec{a} \cdot \vec{b})}{\lVert a \lVert \lVert b \lVert} cos(θ)=∥a∥∥b∥(a⋅b)
可以判断两个向量的距离、分向量与判断向量前后
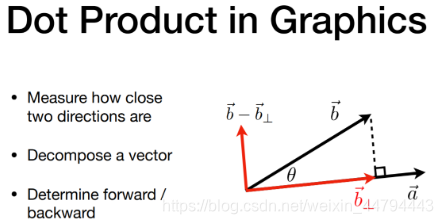
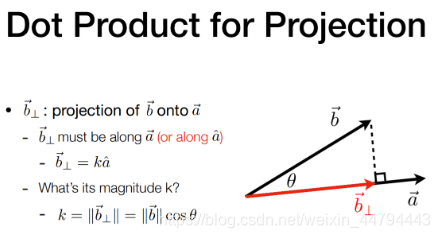
(2) 投影
一个向量在另一个向量上的投影
Cross Product
[1] 右手坐标系
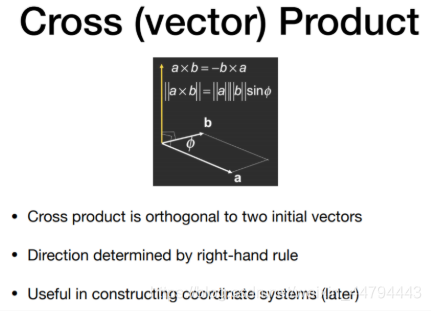
右手坐标系
叉乘在图形学中的应用
(1) 判断一个向量在另一个向量的左右,叉乘为正(与右手方向一致),则为目标在自己右方,反之亦然;
(2) 在性质(1)的基础上,如果一个点在包围他的所有线的同一侧,那么可以说明该点在这个图形内,反之亦然。
矩阵
矩阵转置与逆
(1) 矩阵A、B乘积的转置等于B的转置矩阵乘A的转置矩阵
( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT
(2) 矩阵AB的逆等于B的逆乘A的逆
( A B ) − 1 = B − 1 A − 1 (AB)^{-1} = B^{-1}A^{-1} (AB)−1=B−1A−1
基础变换(二维)
三维变化与二维变换矩阵类似
齐次坐标下的基础变换
Scale:
S ( s x , s y ) = ( s x 0 0 0 s y 0 0 0 1 ) S(s_x,s_y) =\begin{pmatrix} s_x &0 &0\\ 0 & s_y & 0 \\ 0&0&1 \end{pmatrix} S(sx,sy)=⎝⎛sx000sy0001⎠⎞
Rotation:
R ( α ) = ( cos α − sin α 0 sin α cos α 0 0 0 1 ) R(\alpha) = \begin{pmatrix} \cos\alpha& - \sin\alpha & 0 \\ \sin\alpha & \cos \alpha &0 \\ 0&0&1 \end{pmatrix} R(α)=⎝⎛cosαsinα0−sinαcosα0001⎠⎞
Translation:
T ( t x , t y ) = ( 1 0 t x 0 1 t y 0 0 1 ) T(t_x,t_y)=\begin{pmatrix} 1 & 0 & t_x \\ 0 &1& t_y\\ 0 &0& 1 \end{pmatrix} T(tx,ty)=⎝⎛100010txty1⎠⎞
组合变换(Compositon Transform)
矩阵变换把先变化的矩阵放到右边:矩阵运算是从右向左
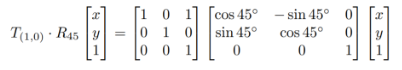
四元数与旋转公式
四元数
罗德里格斯旋转公式
Rodrigue’s Rotation Formula: Raotation by angle α \alpha α around axis n ⃗ \vec{n} n
R ( n ⃗ , α ) = c o s ( α ) I + ( 1 − c o s ( α ) ) n n T + sin ( α ) ( 0 − n z n y n z 0 − n x − n y n x 0 ) ⏟ N R(\vec{n},\alpha)=cos(\alpha)I+(1-cos(\alpha))nn^{T}+\sin(\alpha) \begin{matrix} \underbrace{ \begin{pmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{pmatrix} } \\ N\end{matrix} R(n,α)=cos(α)I+(1−cos(α))nnT+sin(α)
⎝⎛0nz−ny−nz0nxny−nx0⎠⎞N
In the formula
I :Identity matrix
最后乘积的结果是一个3*3的矩阵

MVP变换
Model Transformation
引用博客:MVP变换
对模型进行模型变换时,需要注意坐标系是在世界坐标系原点。当绕模型中心进行变换时,首先要将模型的中心点移动到世界坐标系的原点,之后在进行模型变换,之后移回到原来的位置。
矩阵描述为: M = M t − 1 M r M s M t M=M_t^{-1} M_r M_s M_t M=Mt−1MrMsMt
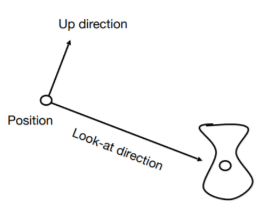
View/Camera Transformation
这个过程是将确定相机的位置:将相机的位置通过下面的过程移动到固定的点和方向。
(1) 相机的位置固定在世界坐标系的原点: e ⃗ \vec{e} e
(2) 相机的朝向 − Z ⃗ -\vec{Z} −Z: g ^ \hat{g} g^
(3) 相机的向上方向 Y ⃗ \vec Y Y: t ^ \hat t t^
基于上述过程,要求视图变换矩阵 M v i e w M_{view} Mview分别求相机的平移矩阵 T v i e w T_{view} Tview、旋转矩阵 R v i e w R_{view} Rview
T v i e w = [ 1 0 0 − x e ⃗ 0 1 0 − y e ⃗ 0 0 1 − z e ⃗ 0 0 0 1 ] T_{view} = \begin{bmatrix} 1 & 0 & 0 & -x_{\vec{e}} \\ 0 & 1 & 0 & -y_{\vec{e}} \\ 0 & 0 & 1 & -z_{\vec{e}} \\ 0 & 0 & 0 & 1 \end{bmatrix} Tview=⎣⎢⎢⎡100001000010−xe−ye−ze1⎦⎥⎥⎤
求旋转矩阵时,直接求相机旋转到原点的矩阵不容易求解,但求原点到相机位置的旋转矩阵容易求。
所以先求原点到相机的旋转矩阵:Z To − g ^ -\hat{g} −g^、Y To t ^ \hat{t} t^、最后保证 X ⃗ \vec{X} X To ( g ^ × t ^ ) (\hat g \times \hat t) (g^×t^) 朝向的方向,原因是保证符合右手坐标系。
R v i e w − 1 = [ x g ^ × t ^ x t x − g 0 y g ^ × t ^ x t y − g 0 z g ^ × t ^ x t z − g 0 0 0 0 1 ] R_{view}^{-1}=\begin{bmatrix} x_{\hat{g} \times \hat{t}}&x_{t}&x_{-g}&0\\ y_{\hat{g} \times \hat{t}}&x_{t}&y_{-g}&0\\ z_{\hat{g} \times \hat{t}}&x_{t}&z_{-g}&0\\ 0&0&0&1 \end{bmatrix} Rview−1=⎣⎢⎢⎡xg^×t^yg^×t^zg^×t^0xtxtxt0x−gy−gz−g00001⎦⎥⎥⎤
因为 R v i e w − 1 R_{view}^{-1} Rview−1是正交矩阵,所以逆矩阵和旋转矩阵相同。
R v i e w = [ x g ^ × t ^ y g ^ × t ^ z g ^ × t ^ 0 x t y t z t 0 x − g y − g z − g 0 0 0 0 1 ] R_{view} =\begin{bmatrix} x_{\hat{g} \times \hat{t}}&y_{\hat{g} \times \hat{t}}&z_{\hat{g} \times \hat{t}}&0\\ x_{t}&y_{t}&z_{t}&0\\ x_{-g}&y_{-g}&z_{-g}&0\\ 0&0&0&1 \end{bmatrix} Rview=⎣⎢⎢⎡xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001⎦⎥⎥⎤
所以
M v i e w = R v i e w T v i e w = [ x g ^ × t ^ y g ^ × t ^ z g ^ × t ^ 0 x t y t z t 0 x − g y − g z − g 0 0 0 0 1 ] M_{view} = R_{view} T_{view}= \begin{bmatrix} x_{\hat{g} \times \hat{t}}&y_{\hat{g} \times \hat{t}}&z_{\hat{g} \times \hat{t}}&0\\ x_{t}&y_{t}&z_{t}&0\\ x_{-g}&y_{-g}&z_{-g}&0\\ 0&0&0&1 \end{bmatrix} Mview=RviewTview=⎣⎢⎢⎡xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001⎦⎥⎥⎤
[ 1 0 0 − x e ⃗ 0 1 0 − y e ⃗ 0 0 1 − z e ⃗ 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0 & -x_{\vec{e}} \\ 0 & 1 & 0 & -y_{\vec{e}} \\ 0 & 0 & 1 & -z_{\vec{e}} \\ 0 & 0 & 0 & 1 \end{bmatrix} ⎣⎢⎢⎡100001000010−xe−ye−ze1⎦⎥⎥⎤
Projection Transformation
个人理解投影变换的终极目的是让物体挤压在一个单位大小的平面(空间)内。原因先挖个坑。
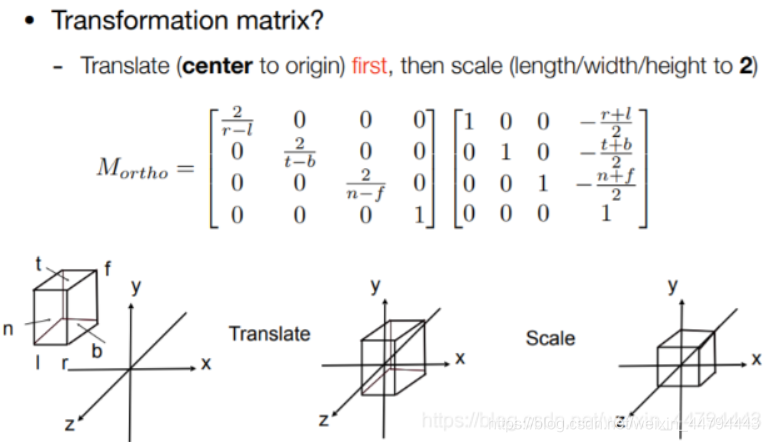
Orthographic Projection
简单理解就是将物体的忽略z坐标,将模型通过Scale To [-1,-1]^2平面内。
真正的操作:
(1) 移动模型的位置到原点
(2) 缩放模型到空间[-1,1]^3中
Perspective Projection
正视投影的光线可以看成是一个立方体,如上图。透视投影的光线可以看成一个视锥,如下图。
透视变换可以分为两个步骤进行:
(1) 将视锥挤压到立方体内 M p e r s p − > o r t h o M_{persp->ortho} Mpersp−>ortho
(2) 将挤压后的视锥进行正视投影变换$M_{ortho}
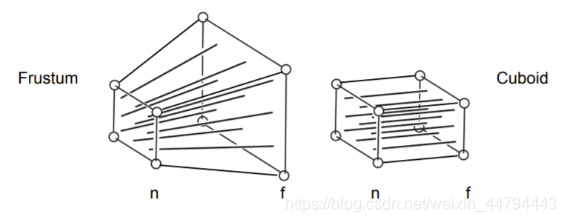
挤压时的变换矩阵 M p e r s p − > o r t h o = [ n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ] M_{persp->ortho}=\begin{bmatrix} n&0&0&0\\ 0&n&0&0\\ 0&0&n+f&-nf\\ 0 & 0&1&0 \end{bmatrix} Mpersp−>ortho=⎣⎢⎢⎡n0000n0000n+f100−nf0⎦⎥⎥⎤
所以投影变换矩阵
M p r o j = M o r t h o M p e r s p − > o r t h o M_{proj}=M_{ortho}M_{persp->ortho} Mproj=MorthoMpersp−>ortho
光栅化
Viewport Transform(视口变换)
将经过MVP变换后得到的单位空间模型变换到屏幕上,屏幕左边是左下角为原点。
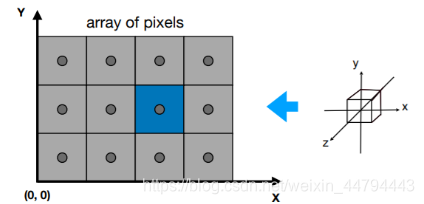
所以视口变换的矩阵
M v i e w p o r t = ( w i d t h 2 0 0 w i d t h 2 0 h e i g h t 2 0 h e i g h t 2 0 0 1 0 0 0 0 1 ) M_{viewport}=\begin{pmatrix} \frac{width}{2}&0&0&\frac{width}{2}\\ 0& \frac{height}{2}&0&\frac{height}{2}\\ 0&0&1&0\\ 0&0&0&1 \end{pmatrix} Mviewport=⎝⎜⎜⎛2width00002height0000102width2height01⎠⎟⎟⎞
Rasterization:Draw to Raster Displays
主要是将已经经过视口变换的模型画在屏幕空间上。
主要过程有:
(1) 采样
(2) 判断像素中心的位置与三角形的关系
采样
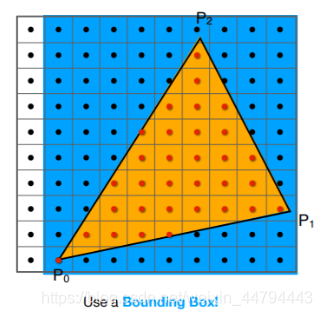
因为屏幕空间本身分辨率已经给出,所以像素点的数量也已经确认了,但是对我们可以通过以下方法提高效率,将可能有用的像素点选取出来:
1.Bounding Box
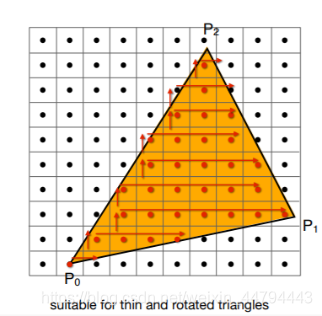
2.Incremental Triangle Traversal
判断像素中心的位置与三角形的关系
主要应用的原理是利用向量的叉乘判断点是否在三角形内。
伪代码如下
for(int x =0 ;x<xmax;x++)
for(int y = 0;y<ymax;y++)
image[x][y]=inside(tri,x+0.5,y+0.5)
反走样与深度缓冲
Artifacts(瑕疵) in Computer Graphics
产生Artifacts的分类和原因
(1) Jaggies(Staircase Pattern)
原因:空间采样产生的锯齿
(2) Mpire
原因:图片欠采样
(3) Wagon Wheel Effect
原因:时间上采样产生
解决办法
(1) 提高采样率:不实用
(2) 反走样
反走样
反锯齿的思路是先模糊,后采样,顺序不可以调换。
走样的原因:采样频率满足奈奎斯特采样定律,即采样频率高于二倍的最高频率。
滤波
频率图:越靠近中心点,表示的频率越低
滤波器的种类大致分为四类:
(1) 低通滤波:应用的效果是模糊
(2) 高通滤波:应用效果是提取边缘信息
(3) 带通滤波:也可以绘制出图像的边缘信息
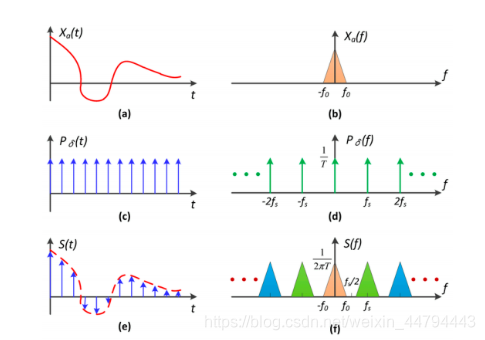
卷积定理
时域卷积、频域相乘
时域卷积,频率图向两边拓展。
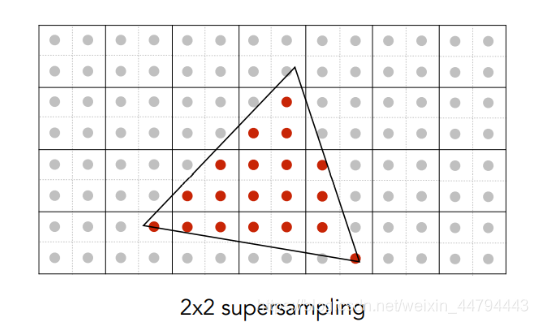
MSAA
通过MSAA方法可以首先模糊的效果。
步骤如下:
(1) 将每个像素点再进行细分
(2) 判断一个像素点里有几个细分的点在三角形内
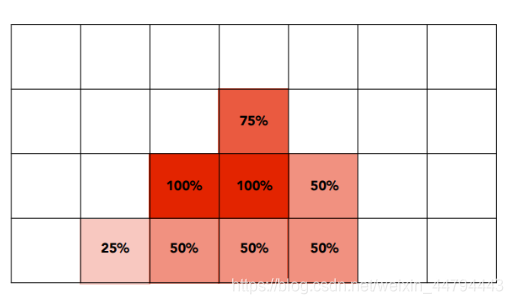
(3) 将像素点根据在三角星内部细分点不同程度的着色,表示已经模糊。
上述过程的流程图如下:
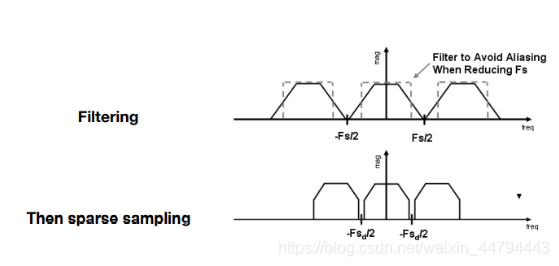
上述过程在频率上的过程相当于低通滤波
Z-Buffer深度缓冲
每个像素都有一个z值代表像素点的深度、z值越大,说明该点越远。
Z-Buffer 算法伪代码
Initalize depth buffer to ∞ \infty ∞
for(each trangle T)
for(each sample(x,y,z) in T)
if(z<zbuffer[x,y]) //closeet samnple so far
zbuffer[x,y]=z; //update color
framebuffer[x,y]=rgb; //update depth
总结
本周主要是完成光栅化的过程。其中比较重要的几个知识点:向量点乘和叉乘的几何意义、齐次坐标系下的矩阵变换、MVP变换、视口变换、光栅化、反走样、Z-Buffrer深度缓冲等等基础概念。