文章目录
Theory behind GAN
之前在 机器学习-34-Generative Adversarial Network(GAN,生成式对抗网络)里面写了一下GAN的大概原理,不过没有具体写GAN背后的数学理论,这一篇尝试详细地推到一下GAN是怎么来的。
考虑一下,GAN到底生成的是什么呢?比如说,假如我们想要生成一些人脸图,实际上,我们是想找到一个分布,从这个分部内sample出来的图片,像是人脸,而不属于这个distribution的分布,生成的就不是人脸。而GAN要做的就是找到这个distribution。

在GAN出生之前,我们怎么做这个事情呢?
之前用的是Maximum Likelihood Estimation,最大似然估计来做生成的,我们先看一下最大似然估计做的事情。
Maximum Likelihood Estimation(最大似然估计)
最大似然估计的理念是,假如说我们的数据集的分布是 P d a t a ( x ) P_{data}(x) Pdata(x) ,我们定义一个分布 P G ( x ; θ ) P_G(x;\theta) PG(x;θ) ,我们想要找到一组参数 θ \theta θ ,使得 越 P G ( x ; θ ) P_G(x;\theta) PG(x;θ)接近 P d a t a ( x ) P_{data}(x) Pdata(x) 越好。比如说,加入 P G ( x ; θ ) P_G(x;\theta) PG(x;θ) 如果是一个高斯混合模型,那么 θ \theta θ 就是均值和方差。

具体怎么操作呢
- 首先我们不知道真实的数据分布是什么样的,但是我们可以从 P d a t a ( x ) P_{data}(x) Pdata(x) 抽样出一些样本(真实图片)
- 对每一个sample出来的x, 我们都可以计算它的likelihood,也就是给定一组参数 θ \theta θ ,我们就能够知道 P G ( x ; θ ) P_G(x;\theta) PG(x;θ)长什么样,然后我们就可以计算出在这个分布里面sample出某一个x的几率。
- 我们把在某个分布可以产生 x i x_i xi的likelihood乘起来,可以得到总的likelihood: L = ∏ i = 1 m P G ( x i ; θ ) L = \prod_{i=1}^m P_G(x^i;\theta) L=∏i=1mPG(xi;θ),我们要找到一组 θ ∗ \theta^* θ∗,可以最大化 L L L
MLE=Minimize KL Divergence
其实最大似然估计的另一种解释是Minimize KL Divergence
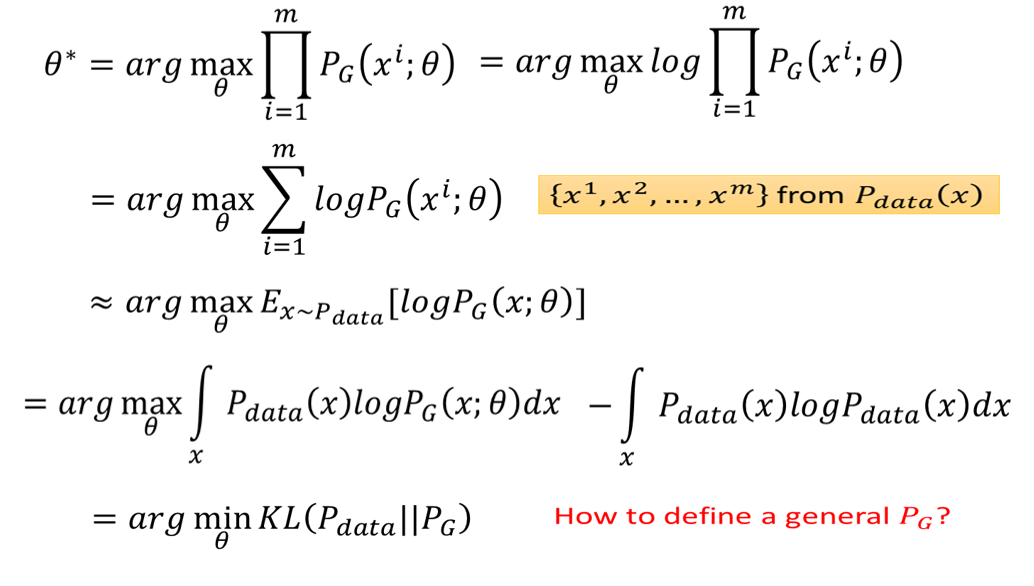
前面我们已经解释过,我们要找到一组 θ ∗ \theta^* θ∗ ,使得 θ ∗ = a r g max θ ∏ i = 1 m P G ( x i , θ ) \theta^* = arg\max\limits_{\theta}\prod_{i=1}^mP_G(x_i,\theta) θ∗=argθmax∏i=1mPG(xi,θ) ,我们对其最一些变换, 加一个Log,再把Log乘进去:
θ ∗ = a r g max θ ∏ i = 1 m P G ( x i ; θ ) = a r g max θ l o g ∏ i = 1 m P G ( x i ; θ ) = a r g max θ ∑ i = 1 m l o g P G ( x i ; θ ) \begin{aligned} \theta^* = & arg \max\limits_{\theta}\prod^{m}_{i=1}P_G(x_i;\theta) = arg \max\limits_{\theta}log\prod^{m}_{i=1}P_G(x_i;\theta) \\ = & arg \max\limits_{\theta}\sum^{m}_{i=1}logP_G(x_i;\theta) \end{aligned} θ∗==argθmaxi=1∏mPG(xi;θ)=argθmaxlogi=1∏mPG(xi;θ)argθmaxi=1∑mlogPG(xi;θ)
其中, ∑ i = 1 m \sum_{i=1}^m ∑i=1m 就相当于我从 P d a t a ( x ) P_{data}(x) Pdata(x) 中sample出m个样本出来。
这个事情就相当于求从 P d a t a ( x ) P_{data}(x) Pdata(x)采样出 x x x的期望:
≈ a r g max θ E x ∼ P d a t a [ l o g P G ( x ; θ ) ] ≈ arg\max\limits_{\theta}E_{x\sim P_{data}}[logP_G(x;\theta)] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ≈argθmaxEx∼Pdata[logPG(x;θ)]
接下来我们把 E x ∼ P d a t a E_{x\sim P_{data}} Ex∼Pdata 这一项展开,做一个积分,得到:
= a r g max θ ∫ x P d a t a l o g P G ( x ; θ ) d x = arg\max\limits_{\theta}\int_xP_{data}logP_G(x;\theta)dx \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =argθmax∫xPdatalogPG(x;θ)dx
接下来我们在上个式子的基础上加一项和 θ \theta θ 无关的项,不影响求最大值:
= a r g max θ ∫ x P d a t a l o g P G ( x ; θ ) d x − ∫ x P d a t a l o g P d a t a ( x ) d x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = arg\max\limits_{\theta}\int_xP_{data}logP_G(x;\theta)dx - \int_xP_{data}logP_{data}(x)dx =argθmax∫xPdatalogPG(x;θ)dx−∫xPdatalogPdata(x)dx
为什么要加上这一项看上去没用的项呢?因为加上这一项后,会发现把 ∫ x P d a t a \int_xP_{data} ∫xPdata提取出来,就是一个 P d a t a P_{data} Pdata和 P G P_G PG 的KL divergence,这里把两个分布位置换一下,就变成求最小值。数学上KL divergence使用来衡量两个分布的差异程度的,那么现在我们的目标就是找一组 θ \theta θ 来最小化 P d a t a P_{data} Pdata 和 P G P_G PG 的KL divegence:
= a r g max θ K L ( P d a t a ∣ ∣ P G ) = arg\max\limits_{\theta}KL(P_{data} || P_G) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =argθmaxKL(Pdata∣∣PG)
但是我们常常要先假定一个具体的分布去逼近实际分布,我们的分布 P G P_G PG 不一定是高斯分布,如果 P G P_G PG 是一个NN,就没有办法算likelihood。因此我们需要一个通用的分布,去逼近这个复杂的图像真实分布。因此要用GAN的Generator来解决这个问题。
Generator
过去如果使用最大似然估计,采用高斯混合模型定义 P G P_G PG ,生成的图片会非常模糊。而现在我们用的Generator的方法,是从一个简单的分布(比如正态分布)中sample出样本,然后扔进一个network(即generator),然后得到输出,把这些输出统统集合起来,我们会得到一个distribution, 这个distribution就是我们要找的 P G P_G PG ,而我们的目标是使得 P G P_G PG 与 P d a t a P_{data} Pdata 越接近越好。

优化目标是最小化 P G P_G PG 与 P d a t a P_{data} Pdata 之间的差异:
G ∗ = a r g max G D i v ( P G , P d a t a ) G^* = arg \max\limits_G Div(P_G,P_{data}) G∗=argGmaxDiv(PG,Pdata)
那么怎么计算两个分布的差异呢? P G P_G PG 与 P d a t a P_{data} Pdata 的公式我们都是不知道的,怎么算呢?这里就要引出Discriminator了:
Discriminator
虽然我们不知道 P G P_G PG 与 P d a t a P_{data} Pdata 的公式,但是我们可以从这两个分布中sample出一些样本出来。对于 P d a t a P_{data} Pdata 来说,我们从给定的数据集中sample出一些样本就可以了。对于 P G P_G PG 来说,我们随机sample一些向量,扔到Generator里面,然后generator会输出一些图片,这就是从 P G P_G PG 里面sample了。

问题就变成我们怎么从sample的数据求 P G P_G PG 与 P d a t a P_{data} Pdata
其实我们可以使用Discriminator来衡量 P G P_G PG 与 P d a t a P_{data} Pdata 的Divergence
蓝色星星: data sampled from P d a t a P_{data} Pdata
橙色星星: data sampled from P G P_G PG

我们可以用Discriminator来区分两个Distribution,公式:
V ( G , D ) = E x ∼ P d a t a [ l o g D ( x ) ] + E x ∼ P G [ l o g ( 1 − D ( x ) ) ] V(G,D) = E_{x\sim P_{data}}[logD(x)]+E_{x\sim P_G}[log(1-D(x))] V(G,D)=Ex∼Pdata[logD(x)]+Ex∼PG[log(1−D(x))]
前面一项是表示数据sampled from P d a t a P_{data} Pdata ,值越大越好,后面一项是表示数据sampled from P G P_G PG,值越小越好
上面公式的形式和训练一个二分类Classifier的目标函数长得一样,就是说可以把 P G P_G PG 与 P d a t a P_{data} Pdata 看成两个分类。
训练Discriminator就好比训练一个二分类:
D ∗ = a r g max D V ( D , G ) D^* = arg \max\limits_DV(D,G) D∗=argDmaxV(D,G)
而训练出来的 max D V ( D , G ) \max\limits_D V(D,G) DmaxV(D,G)就相当于与JS divergence,来看下为什么是JS divergence。
如果两个分布的数据很接近(small divergence),那么Discriminator很难把数据分开,也就是上面的公式很难找到一个D,使得 D ∗ D^* D∗取得很大的值。那么就找到最大的divergence,使得两个分布的数据相隔ed远一些,我们的Discriminator就能容易的将数据分开。

也就是 D ∗ D^* D∗ 和divergence程度有关系,下面用数学来证明。
D*和divergence的关系证明

给定Generator, 我们要找到能最大化目标函数 V ( D , G ) V(D,G) V(D,G) 的 D ∗ D^* D∗ :
V = E x ∼ P d a t a [ l o g D ( x ) ] + E x ∼ P G [ l o g ( 1 − D ( x ) ) ] = ∫ x P d a t a ( x ) l o g D ( x ) d x + ∫ x P G ( x ) l o g ( 1 − D ( x ) ) d x = ∫ x [ P d a t a ( x ) l o g D ( x ) ] + P G ( x ) l o g ( 1 − D ( x ) ) ] d x \begin{aligned} V = & E_{x\sim P_{data}}[logD(x)]+E_{x\sim P_G}[log(1-D(x))] \\ = & \int_xP_{data}(x)logD(x)d_x + \int_xP_G(x)log(1-D(x))d_x \\ = & \int_x[P_{data}(x)logD(x)]+P_G(x)log(1-D(x))]d_x \end{aligned} V===Ex∼Pdata[logD(x)]+Ex∼PG[log(1−D(x))]∫xPdata(x)logD(x)dx+∫xPG(x)log(1−D(x))dx∫x[Pdata(x)logD(x)]+PG(x)log(1−D(x))]dx
上面等同于,我们将某一个X拿出来,我们可以让之前积分内部的式子越大越好;其实就是所有的X就是分开来算;
P d a t a ( x ) l o g D ( x ) + P G l o g ( 1 − D ( x ) ) P_{data}(x)logD(x) + P_Glog(1-D(x)) Pdata(x)logD(x)+PGlog(1−D(x))

我们想要找到一组参数 D ∗ D^* D∗ ,让这一项最大。我们把这个式子简写一下,将 P d a t a P_{data} Pdata 用a表示, P G P_G PG 用b表示,那么上式可写为:
f ( D ) = a l o g D + b l o g ( 1 − D ) f(D) = alogD+blog(1-D) f(D)=alogD+blog(1−D)
接下来对其求导,并让其等于=0,即求梯度,有:
d f ( D ) d D = a × 1 D + b × 1 1 − D × ( − 1 ) = 0 \frac{df(D)}{dD} = a × \frac{1}{D} +b × \frac{1}{1-D} × (-1) = 0 dDdf(D)=a×D1+b×1−D1×(−1)=0
最终求解得到 D ∗ D^* D∗ :
D ∗ = a a + b = P d a t a ( x ) P d a t a ( x ) + P G ( x ) D^* = \frac{a}{a+b} = \frac{P_{data}(x)}{P_{data}(x)+P_G(x)} D∗=a+ba=Pdata(x)+PG(x)Pdata(x)
我们求出了这个D,把它代到 V ( G , D ∗ ) V(G,D^*) V(G,D∗) 里面,然后将分子分母同时除以2,然后提出来(这一步是为了之后方便化简),之后可以将其化简成Jensen-Shannon divergence(某一种计算分部差异的公式)的形式:
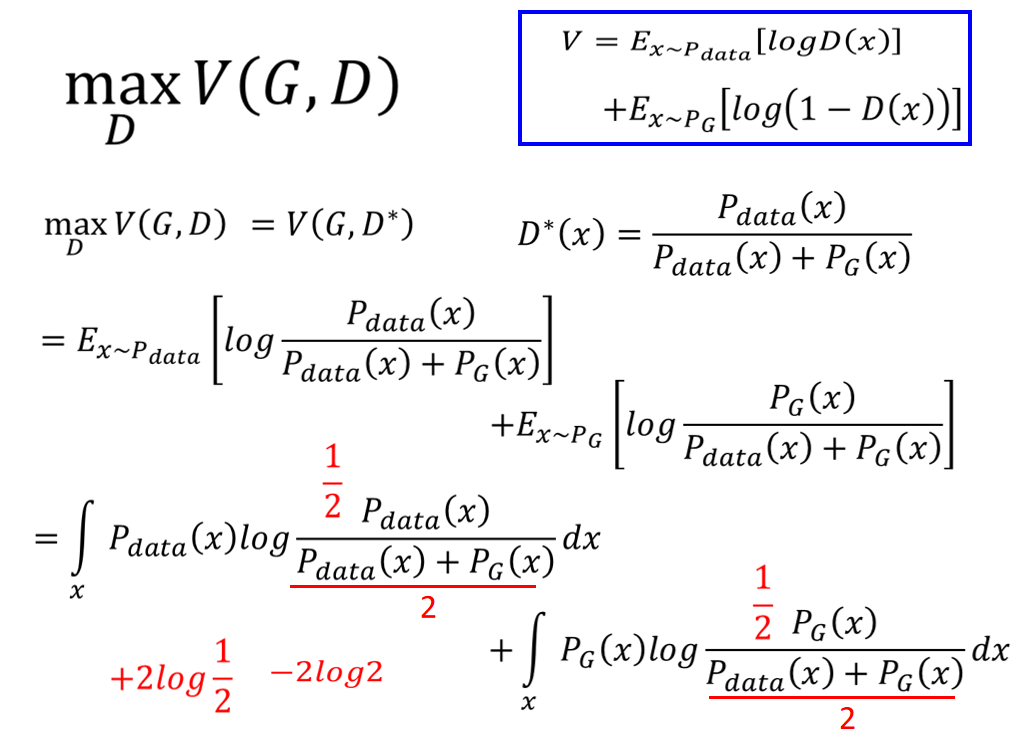
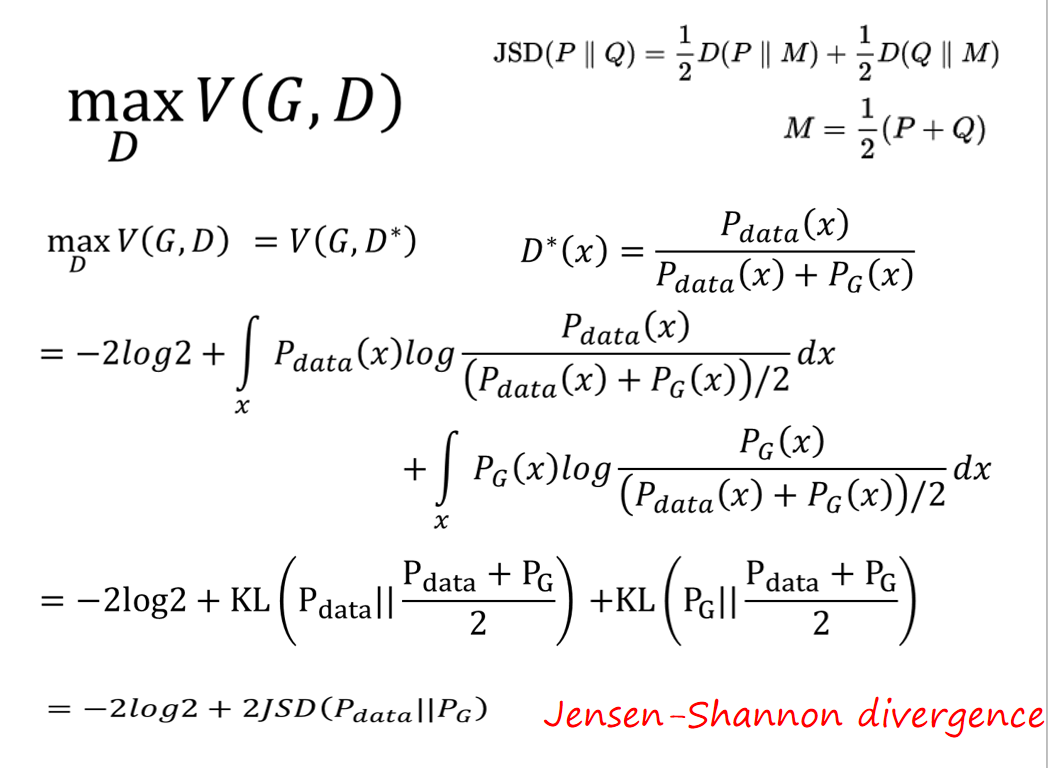
max D V ( G , D ) = V ( G , D ∗ ) = E x ∼ P d a t a [ l o g P d a t a ( x ) P d a t a ( x ) + P G ( x ) ] + E x ∼ P G [ l o g P G ( x ) P d a t a + P G ( x ) ] = ∫ x P d a t a ( x ) l o g 1 2 P d a t a ( x ) P d a t a ( x ) + P G ( x ) 2 d x + ∫ x P G ( x ) l o g 1 2 P G ( x ) P d a t a ( x ) + P G ( x ) 2 d x = l o g 1 2 + l o g 1 2 + ∫ x P d a t a ( x ) l o g P d a t a ( x ) P d a t a ( x ) + P G ( x ) 2 d x + ∫ x P G ( x ) l o g P G ( x ) P d a t a ( x ) + P G ( x ) 2 d x = 2 l o g 1 2 + ∫ x P d a t a ( x ) l o g P d a t a ( x ) P d a t a ( x ) + P G ( x ) 2 d x + ∫ x P G ( x ) l o g P G ( x ) P d a t a ( x ) + P G ( x ) 2 d x = − 2 l o g 2 + ∫ x P d a t a ( x ) l o g P d a t a ( x ) P d a t a ( x ) + P G ( x ) 2 d x + ∫ x P G ( x ) l o g P G ( x ) P d a t a ( x ) + P G ( x ) 2 d x = − 2 l o g 2 + K L ( P d a t a ∣ ∣ P d a t a + P G 2 ) + K L ( P G ∣ ∣ P d a t a + P G 2 ) = − 2 l o g 2 + 2 J S D ( P d a t a ∣ ∣ P G ) \begin{aligned} \max\limits_DV(G,D) = & V(G,D^*) \\ = & E_{x\sim P_{data}}[log\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}]+E_{x\sim P_G}[log\frac{P_G(x)}{P_{data}+P_G(x)}] \\ = & \int_xP_{data}(x)log\frac{\frac{1}{2}P_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2}}d_x + \int_xP_{G}(x)log\frac{\frac{1}{2}P_{G}(x)}{\frac{P_{data}(x)+P_{G}(x)}{2}}d_x \\ = & log\frac{1}{2}+log\frac{1}{2} + \int_xP_{data}(x)log\frac{P_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2}}d_x + \int_xP_{G}(x)log\frac{P_{G}(x)}{\frac{P_{data}(x)+P_{G}(x)}{2}}d_x \\ = & 2log\frac{1}{2} + \int_xP_{data}(x)log\frac{P_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2}}d_x + \int_xP_{G}(x)log\frac{P_{G}(x)}{\frac{P_{data}(x)+P_{G}(x)}{2}}d_x \\ = & -2log2 + \int_xP_{data}(x)log\frac{P_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2}}d_x + \int_xP_{G}(x)log\frac{P_{G}(x)}{\frac{P_{data}(x)+P_{G}(x)}{2}}d_x \\ = & -2log2+KL(P_{data}||\frac{P_{data}+P_G}{2})+KL(P_G||\frac{P_{data}+P_{G}}{2}) \\ = & -2log2+2JSD(P_{data}||P_G) \end{aligned} DmaxV(G,D)========V(G,D∗)Ex∼Pdata[logPdata(x)+PG(x)Pdata(x)]+Ex∼PG[logPdata+PG(x)PG(x)]∫xPdata(x)log2Pdata(x)+PG(x)21Pdata(x)dx+∫xPG(x)log2Pdata(x)+PG(x)21PG(x)dxlog21+log21+∫xPdata(x)log2Pdata(x)+PG(x)Pdata(x)dx+∫xPG(x)log2Pdata(x)+PG(x)PG(x)dx2log21+∫xPdata(x)log2Pdata(x)+PG(x)Pdata(x)dx+∫xPG(x)log2Pdata(x)+PG(x)PG(x)dx−2log2+∫xPdata(x)log2Pdata(x)+PG(x)Pdata(x)dx+∫xPG(x)log2Pdata(x)+PG(x)PG(x)dx−2log2+KL(Pdata∣∣2Pdata+PG)+KL(PG∣∣2Pdata+PG)−2log2+2JSD(Pdata∣∣PG)
通过这一系列的化简,我们可以知道,最大化 V ( G , D ∗ ) V(G,D^*) V(G,D∗) ,其实就是求解分布 P d a t a , P G P_{data},P_G Pdata,PG 的JS divergence。所以当去训练一个distriminator,就是通过 P d a t a , P G P_{data},P_G Pdata,PG sample出来的样本去求这两个分布的差异。
KL散度、JS散度和交叉熵(知识扩展)
KL散度、JS散度和交叉熵:三者都是用来衡量两个概率分布之间的差异性的指标。不同之处在于它们的数学表达。
对于概率分布P(x)和Q(x)
-
KL散度(Kullback–Leibler divergence)又称KL距离,相对熵。
当P(x)和Q(x)的相似度越高,KL散度越小。
KL散度主要有两个性质:- 不对称性
尽管KL散度从直观上是个度量或距离函数,但它并不是一个真正的度量或者距离,因为它不具有对称性,即D(P||Q)!=D(Q||P)。 - 非负性
相对熵的值是非负值,即D(P||Q)>0。
- 不对称性
-
JS散度(Jensen-Shannon divergence)JS散度也称JS距离,是KL散度的一种变形。
但是不同于KL主要又两方面:- 值域范围
JS散度的值域范围是[0,1],相同则是0,相反为1。相较于KL,对相似度的判别更确切了。 - 对称性
即 JS(P||Q)=JS(Q||P),从数学表达式中就可以看出。
- 值域范围
-
交叉熵(Cross Entropy)
在神经网络中,交叉熵可以作为损失函数,因为它可以衡量P和Q的相似性。
交叉熵和相对熵的关系:
以上都是基于离散分布的概率,如果是连续的数据,则需要对数据进行Probability Density Estimate来确定数据的概率分布,就不是求和而是通过求积分的形式进行计算了。
G*
生成器训练的目标是找到一个 G ∗ G^* G∗ ,去最小化 P G P_G PG 与 P d a t a P_{data} Pdata 的差异。也就是:
G ∗ = a r g max G D i v ( P G , P d a t a ) G^* = arg \max\limits_G Div(P_G,P_{data}) G∗=argGmaxDiv(PG,Pdata)
而这个divergence我们没有办法直接去算,我们不知道 P G P_G PG 与 P d a t a P_{data} Pdata 的公式具体是什么。于是我们通过一个discriminator来计算两个分布间的差异:
D ∗ = a r g max D ( D , G ) D^* = arg \max\limits_D(D,G) D∗=argDmax(D,G)
那么我们的优化目标就变为:
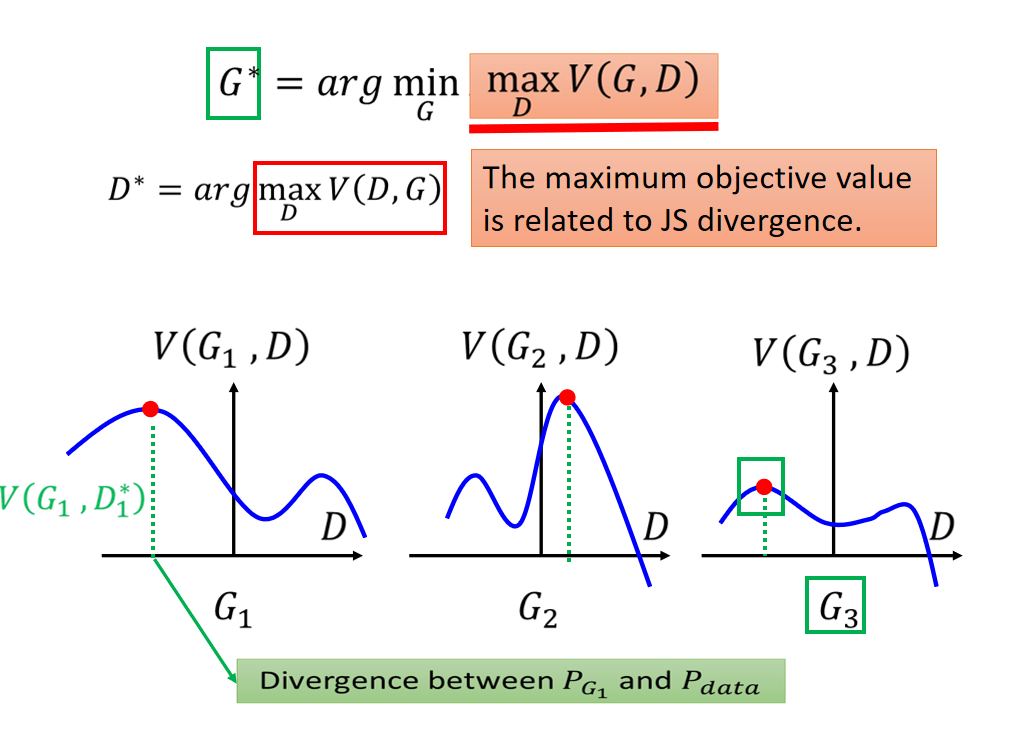
G ∗ = a r g min G max D V ( G , D ) G^* = arg \min\limits_G \max\limits_DV(G,D) G∗=argGminDmaxV(G,D)
这个看起来很复杂,其实直观理解一下,如下图,我们假设已经把Generator固定住了,图片的曲线表示,红点表示固定住G后的 max D V ( G , D ) \max\limits_DV(G,D) DmaxV(G,D) , 也就是 P G P_G PG 与 P d a t a P_{data} Pdata 的差异。而我们的目标是最小化这个差异,所以下图的三个网络中, G 3 G_3 G3是最优秀的。
GD Algorithm for GAN
具体的算法:

- Step1:首先固定生成器,找到一个能够使V最大的D;
- Step:然后固定D,找到能够使这个最大D情况下V最小的G。不停的迭代…
从数学看为什么这个算法是在解上面的最小最大过程:
用函数 L ( G ) L(G) L(G)替代 G ∗ G^* G∗ 中的 max D V ( G , D ) \max\limits_DV(G,D) DmaxV(G,D) :
G ∗ = a r g min G L ( G ) G^* = arg\min\limits_GL(G) G∗=argGminL(G)
那么找最好的G的话就用梯度下降(和一般的train是一样的);θ是表示G的参数
但是L(G)有个max操作,但是它依然也是可以做微分的: 假设有个函数f(x)是max三个子函数,f(x)其实 就是每个阶段取最大值 最终求微分的过程就是在每一个点x,先看哪个子函数在这个点最大,微分值就是最大的那个子函数的微分值。也就是梯度下降依然适用,就是每次更新参数的时候先看自己在那个范围,再用这个范围的函数求梯度,然后更新;重复…
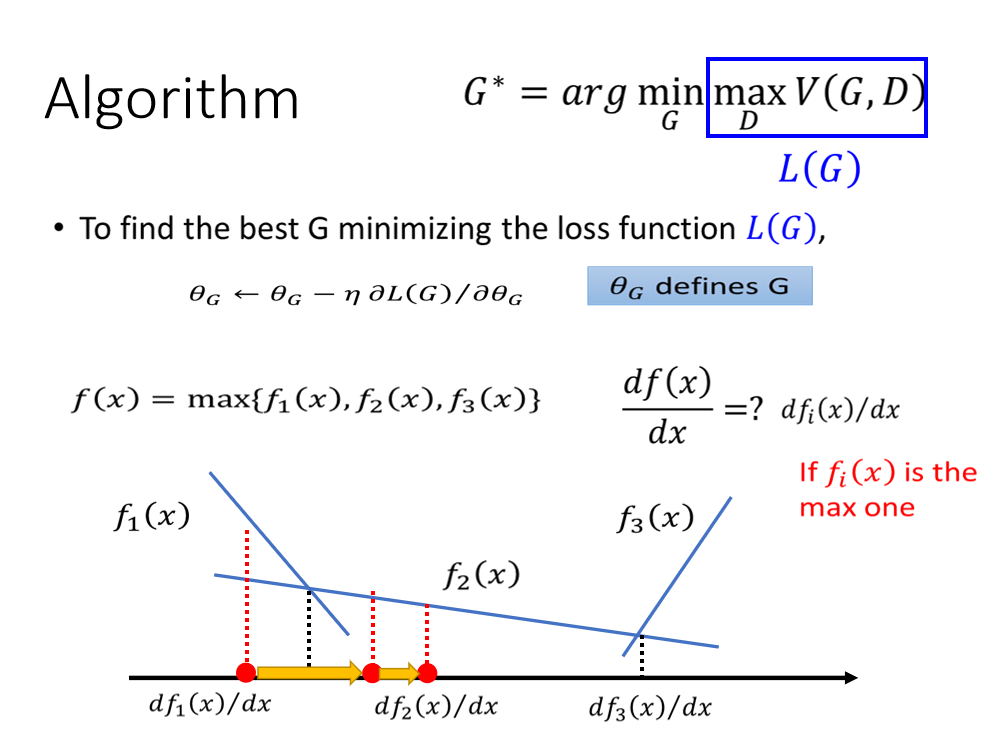
也就是说函数中有max操作,也是可以做梯度下降的。
明白这个之后我们继续来看整个 G ∗ G^* G∗ 如何算:
-
给定一个 G 0 G_0 G0
-
找到可以使得 V ( G 0 , D ) V(G_0,D) V(G0,D) 最大的 D ∗ D^* D∗ ,这个过程可以用梯度上升来求解。 V ( G 0 , D 0 ∗ ) V(G_0,D_0^*) V(G0,D0∗) 就是在求 P G P_G PG 与 P d a t a P_{data} Pdata 的JS divergence(前面已经证明过了)
-
找到 max D V ( G , D ) \max\limits_DV(G,D) DmaxV(G,D) 后,对 G ∗ = a r g min G max D V ( G , D ) G^* = arg \min\limits_G\max\limits_DV(G,D) G∗=argGminDmaxV(G,D) 求导, θ G ← θ G − η ∂ V ( G , D 0 ∗ ) ∂ θ G \theta_G \leftarrow \theta_G - \eta\frac{\partial{V(G,D_0^*)}}{\partial\theta_G} θG←θG−η∂θG∂V(G,D0∗) 更新参数得到 G 1 G_1 G1 , 这个过程其实是在最小化JSd ivergence
-
重新寻找 D 1 ∗ D_1^* D1∗可以最大化 V ( G 1 , D ) V(G_1,D) V(G1,D)。这个过程求的是 P G P_G PG 与 P d a t a P_{data} Pdata 的JS divergence
-
θ G ← θ G − η ∂ V ( G , D 1 ∗ ) ∂ θ G \theta_G \leftarrow \theta_G - \eta\frac{\partial{V(G,D_1^*)}}{\partial\theta_G} θG←θG−η∂θG∂V(G,D1∗) 得到 G 1 G_1 G1, 这个过程可以看做是在最小化JS divergence,这个过程需要注意不要让 G G G 变化得太大,尽量让 G 0 , G 1 G_0,G_1 G0,G1的差别不要太大(下面的注意说明了原因)。这也是训练过程中的一个tricks
-
然后不断循环……
注意:
其实在train过程中不是真正的minimize JS散度,为什么呢?
刚开始的第一步,先找一个 G 0 G_0 G0,然后找 G 0 G_0 G0的最大V就是 G 0 G_0 G0下的散度; 当你的G在train时变了一点,你的function V(G,D)就变了;此时由于D固定,所以JS散度会变得不再是此刻G下的JS散度了。
因此前提假设是: V ( G 0 , D ) V(G_0,D) V(G0,D)和 V ( G 1 , D ) V(G_1,D) V(G1,D)是很像的;(G的参数变化很小)
因此在train生成器的时候不能更新的太多次,因为这个过程中D是不变的
但是在train判别器的时候要train到底,因为你在找当前G的JS散度。
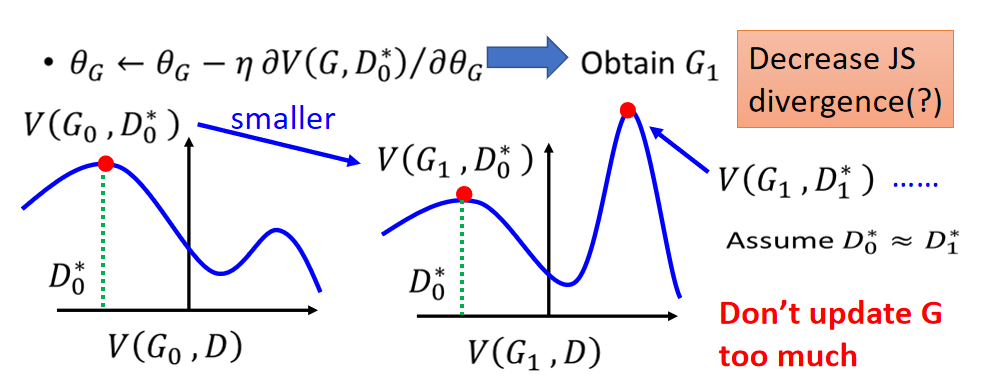
假设在 G 0 G_0 G0的时候, V ( G 0 , D ) V(G_0,D) V(G0,D)的曲线如上图左边所示,然后, D 0 ∗ D_0^* D0∗使得 V ( G 0 , D ) V(G_0,D) V(G0,D)最大,这个时候的JSD是 V ( G 0 , D 0 ∗ ) V(G_0,D_0^*) V(G0,D0∗) between P G P_G PG and P d a t a P_{data} Pdata ,然后我们用梯度下降更新 G 0 G_0 G0,将其变成 G 1 G_1 G1,这个时候由于G的值变化后, V ( G 1 , D ) V ( G_1 , D ) V(G1,D) 的曲线发生了变化(参考上面$f ( x ) = \max { f_1 ( x ) , f_2 ( x ) , f_3 ( x ) } 的 例 子 ) , 这 个 新 曲 线 的例子),这个新曲线 的例子),这个新曲线V(G_1,D_1*)$如上图的右边所示,这个时候的最大值就不在$D_0 了 , 离 它 很 远 , 这 个 时 候 的 J S D 变 成 了 了 ,离它很远,这个时候的JSD变成了 了,离它很远,这个时候的JSD变成了V(G_1,D_1^)$ , 可以看到后面的JSD明显要变大了,这样是不对的,因此我们做了假设,假设:
D 0 ∗ ≈ D 1 ∗ D_0^* ≈ D_1^* D0∗≈D1∗
这个时候从, V ( G 0 , D ) V(G_0,D) V(G0,D)到,$V(G_1,D) $的曲线变化不会很大。也就是G这个参数只变化了一点点。
我们同样可以用来 D 0 ∗ D_0^* D0∗ 衡量变化后JSD between P G P_G PG and P d a t a P_{data} Pdata
也就是说GAN的训练技巧:
Generator不要一次update太多,也不需要太多的iteration;
而Discriminator可以训练到收敛。因为要找到最大值才能衡量出JSD。
In practice(实做中)
理论上V是要取期望值,但是实际上是不可能的。只能用样本的均值进行估计:

从 P d a t a ( x ) P_{data}(x) Pdata(x)从抽取样本 { x 1 , x 2 , . . . , x m } \{x^1,x^2,...,x^m\} {
x1,x2,...,xm},从 P G ( x ) P_G(x) PG(x) 中抽取样本 { x ~ 1 , x ~ 2 , . . . , x ~ m } \{\widetilde{x}^1,\widetilde{x}^2,...,\widetilde{x}^m\} {
x
1,x
2,...,x
m}
M a x i m i z e V ~ = 1 m ∑ i = 1 m l o g D ( x i ) + 1 m ∑ i = 1 m l o g ( 1 − D ( x ~ i ) ) Maximize \ \ \ \widetilde{V} = \frac{1}{m}\sum_{i=1}^mlogD(x^i)+\frac{1}{m}\sum_{i=1}^mlog(1-D(\widetilde{x}^i)) Maximize V
=m1i=1∑mlogD(xi)+m1i=1∑mlog(1−D(x
i))
上面这个事情实际上就是在训练一个Binary Classifier,记为D,D后面接一个sigmoid函数,使得输出值在[0,1]之间
我们把 { x 1 , x 2 , . . . , x m } \{x^1,x^2,...,x^m\} { x1,x2,...,xm}from P d a t a ( x ) P_{data}(x) Pdata(x)看做Positive examples;
我们把fr { x ~ 1 , x ~ 2 , . . . , x ~ m } \{\widetilde{x}^1,\widetilde{x}^2,...,\widetilde{x}^m\} { x 1,x 2,...,x m} from generator P G ( x ) P_G(x) PG(x) 看做Negative examples
目标是最小化上面两组数据的Cross-entropy,计算这个交叉熵的公式推导出来就是上面那个公式 V ~ \tilde{V} V~
Algorithm for GAN(Review)
最终的算法:
首先train判别器,实际上没办法train到收敛,可以定义训练k次;(JS散度是什么)
之后train生成器:其中第一项是与生成器无关的,由于G不能训练太多,所以updata一次就好(最小化JS散度)

因为这些步骤在前面的GAN基础中已经说过了,这里就不细说了,我将之前的解说复制了一下:
-
首先初始化判别器和生成器
-
然后从database中抽取m个图片(like batch size);
从一个分布中抽取m个vector
使用m个vector产生m个image。 之后去调整判别器:
首先把m张真实图片都拿出来,经过判别器得到分数,然后经过log再统统平均起来(当然希望这个越大越好,因为希望真实的图片得分高);对于生成器生成的m张图片当然希望值越小越好,因此用1-值,其越大越好。因此使用梯度上升的方法,调节判别器参数。(实际训练过程是给真实图片赋值为1,生成图片赋值为0;训练二分类器;等同于上述过程)
-
从一个分布中抽取m个vector
重新生成m张图片,G(Z)就是一张图片,再把它丢到判别器中D(G(Z));再对所有的生成的求平均,在D不改变的情况下,希望这个值越小越好
Objective Function for Generator in Real Implementation
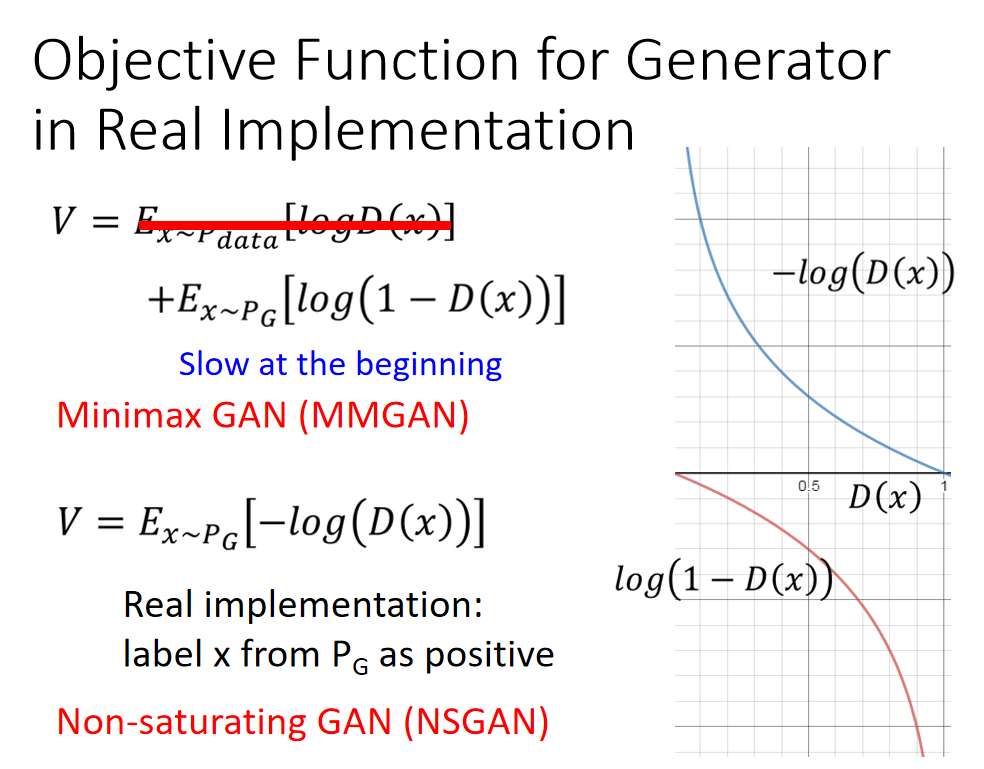
按上面的算法:,我们可以知道Generator目标函数应该是:
V = E x ∼ P d a t a [ l o g D ( x ) ] + E x ∼ P G [ l o g ( 1 − D ( x ) ) ] V = E_{x\sim P_{data}}[logD(x)]+E_{x\sim P_G}[log(1-D(x))] V=Ex∼Pdata[logD(x)]+Ex∼PG[log(1−D(x))]
然后第一项和 G G G函数无关,所以在求最小值的时候可以忽略:
V = E x ∼ P G [ l o g ( 1 − D ( x ) ) ] V = E_{x\sim P_G}[log(1-D(x))] V=Ex∼PG[log(1−D(x))]
但是,在论文原文在实作的时候把这个函数改为:
V = E x ∼ P G [ − l o g ( D ( x ) ) ] V = E_{x\sim P_G}[-log(D(x))] V=Ex∼PG[−log(D(x))]
上图中我们给出了两个函数的图像。
红色曲线对应 l o g ( 1 − D ( x ) ) log(1-D(x)) log(1−D(x)):江湖人称Minimax GAN (MMGAN)
蓝色曲线对应 − l o g ( D ( x ) ) -log(D(x)) −log(D(x)):江湖人称Non-saturating GAN (NSGAN) (saturating /ˈsætʃəreɪtɪŋ/:饱和的;浸透的)
我们可以看到,红色曲线由于刚开始的Generator 没有训练过,它的生成对象都很假,很容易被识破,因此刚开始的 l o g ( 1 − D ( x ) ) log(1-D(x)) log(1−D(x)) 值很小。
不好训练,换成蓝色曲线后,两个曲线都是下降趋势,没有变,但是蓝色曲线刚开始的值很大,适合做梯度下降。
其实后来实验证明两种结果都差不多。
老师给出了他的猜想,蓝色曲线其实就是把label x from P G P_G PG as positive.就是把生成对象和真实对象的标签换一下。估计是作者懒得改code,用的同一套code训练两组data。。。
理论部分到此结束。下面看一些比较直觉的东西。
Intuition
Generator和Discriminator的关系:Discriminator leads the generator.
红线:Discriminator
绿线:Data(target)distribution
蓝线:Generated distribution
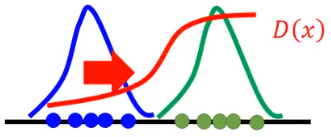
有两组数据,生成对象(蓝色点)、真实对象(绿色点),然后我们训练一个Discriminator,然后Discriminator会给蓝色点比较低的分数,绿色点比较高的分数(红色曲线)。然后蓝色点就会跟着Discriminator的趋势(梯度方向)向右边移动,要获得高分:
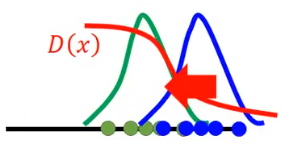
移动过头,没关系,这个时候我们会再训练一次Discriminator,这个时候两个分布比较近,所以Discriminator的loss比较大,也就是两个分布的JS divergence比较小。然后蓝色点就会跟着Discriminator的趋势(梯度方向)向左边移动,直到Discriminator变成直线,就是Discriminator无法分辨生成对象(蓝色点)和真实对象(绿色点)。

GAN会不会出现正负样本不均衡的情况?
答:不会,因为正负样本都是我们自己sample出来的,只要不想自己和自己过不去就可以sample等量的样本。