
上一篇文章谈了一下六张图中的第二张,涉及了正态分布,
本文进入第三张图,具体谈一下队员年龄所表现出来的对数正态分布

C 对数正态分布:队员年龄
上面的六个图,就形态而言,也就是上文的重点讲解的B图,比较像正态分布,
其他的,则都有明显偏离。
以队员年龄图为例,如下图所示,这种分布被称为“右偏”,也称为正偏态.

从上图可见,右边有些所谓的“长尾”数据,属于高龄队员,从图中的峰值可见,众数应该是23岁,
这里,我们延伸讨论一下,大家应该还记得一开始说的,球员的平均年龄是25岁,确切地说,平均数是25.22,而不是23岁。
那么为什么直方图的平均值和峰值会不同呢?
如果“平均”意味着所谓的“典型”,为什么它不等于拥有最多球员的年龄组呢?
原因是认为“平均”总是意味着“典型”是一个统计学上的陷阱,不知多少人一次又一次地掉进这个陷阱。
因为这种分布,是不对称的。
由于在波峰右侧的队员比在左侧的数量更多,这些年长的队员将平均值“拉”到远离波峰的右侧。
而这里的平均值,或者说算术平均值,是所有年龄的总和,除以所有队员数。
年龄中值是25岁,也就是一半的球员年龄大,一半的球员年龄小。当分布向左或向右倾斜时,中值将出现在众数(峰值)和平均值之间。
在这种情况下,如何定义典型?
那么,相对而言,为什么年长球员比年轻球员多呢?
其实,北美职业足球联盟没有最低或最高年龄限制。但是有一项规定---运动员必须高中毕业至少3年才能成为职业运动员。
所以,最年轻的球员可能是20岁,也有19岁的。
而对于球员而言,只要身体允许,或者有能力,就可以一直打球。
顺便说一句,这种分布类似于生存函数的形状,在工程学中,生存函数通常用来表示特定物体——可能是病人或设备——死亡或报废的时间。
如果你把一个足球运动员职业生涯的结束看作是“失败”点,那么每个球员都会尽可能的打球,直到他们打不动为止。
因此,根据球员年龄数据,可以绘制出一个生存函数,
如果时间点足够多,选择好合适的时间单位,这样的图像,不但可以展现出球员参加工作,或隐退的时间,更能读出些人世更替的历史感来。
D 正态分布(有离群值):队员姓名全称中的字符数
我们看下第四张图,
描述的队员姓名全称的字符数量,如下所示,看起来更像一个正态分布,不过略微右偏,而且在图的右侧,零散分布着一些离群值。
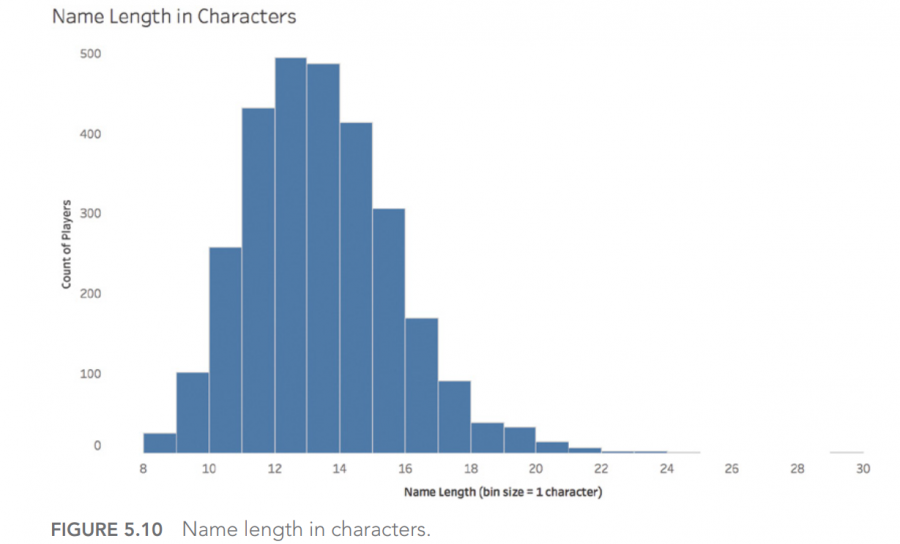
从图中可见,众数,也就是出现次数最多的名字长度是12个字符,比13个字符的队员数量稍微多一点。
但是竟然有一个队员的名字里有29个字符(包括空格和连字符),那就是Christian Scotland-Williamson。
他名字的长度几乎比平均值高出7个标准差。
如果有一个球员的身高与平均身高相差那么远,那么他的身高已经超过了7英尺8英寸。
到这个高度,无疑已经是橄榄球员中的巨人了,即使是在篮球界,也无人能比,有史以来,NBA中最高的两名球员,身高也不过7英尺7英寸而已。
E.多模式分布:队员体重
如下图所示,第五个分布图向我们展示了足球运动员的体重,这是个三峰多模态分布图形。
那么这个奇怪的形状从何而来?
这是一个基于事实的体现:在橄榄球场上,不同的位置往往需要非常不同的体型。
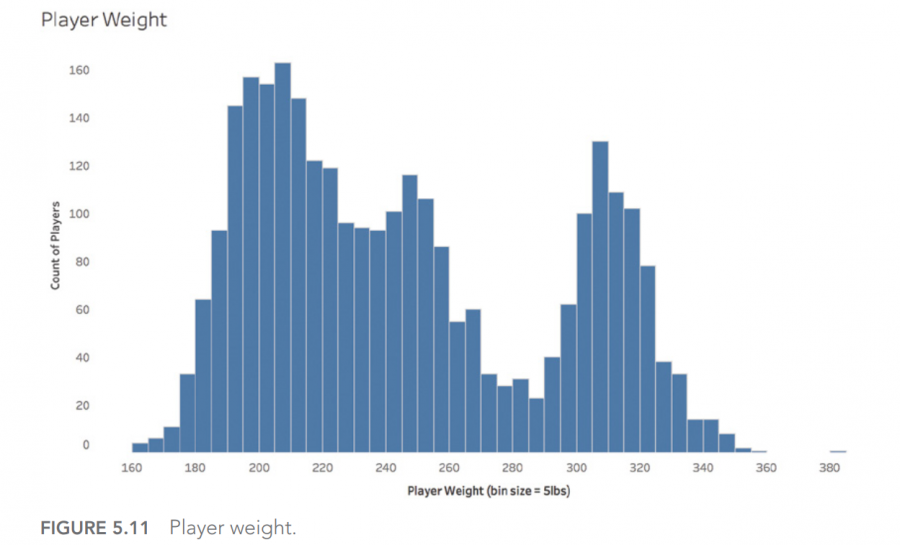
图中三个组中,每组都有将近1000人,
比如,在进攻和防守位置,会有几位"巨人"把守,被称作linemen,以控制中场;也有行动敏捷的接球手与传球手,与四分卫相呼应;还有其他职能的球员。
进一步,把上图打散,作图如下,会直接看到有三组不同体重的人,

球员的平均体重是247.7磅,可以从上面的直方图中容易看出,这是“All Other Positions”类别中相当典型的体重数字,但对于另外两组来说,则不具备代表性,
而这两组人加在一起,大约占了联盟中三分之二的球员。
那么244.7磅是所谓的“标准”吗?显然不是,至少不是对所有的组都适用。
由此可见,就这种多模态,多峰值的分布而言, 或许整体均值可以代表某一分支的情况,但依然不能代表全体的典型性
结语
至此,五张图已经讲完了,是否发现,类似均值,中值这种描述数据整体中心趋势的指标,并不如大家直觉上所期待的那样。
下一篇,我们介绍最后一张图---球员的收入分布图。
