Definition
The gradient of a scalar field ϕ ( x , y , z ) \phi (x,y,z) ϕ(x,y,z) is defined by
g r a d ϕ = ∇ ϕ = i ∂ ϕ ∂ x + j ∂ ϕ ∂ y + k ∂ ϕ ∂ z . grad \phi=\nabla \phi=\boldsymbol{i} \frac{\partial \phi}{\partial x}+\boldsymbol{j} \frac{\partial \phi}{\partial y}+\boldsymbol{k} \frac{\partial \phi}{\partial z}. gradϕ=∇ϕ=i∂x∂ϕ+j∂y∂ϕ+k∂z∂ϕ.
Clearly, ∇ ϕ \nabla \phi ∇ϕ is a vector field whose x x x-, y y y- and z z z- components are the first partial derivatives of ϕ ( x , y , z ) \phi (x,y,z) ϕ(x,y,z) with respect to x x x, y y y and z z z respectively. Also note that the vector field ∇ ϕ \nabla \phi ∇ϕ should not be confused with the vector operator ϕ ∇ \phi \nabla ϕ∇, which has components ( ϕ ∂ / ∂ x , ϕ ∂ / ∂ y , ϕ ∂ / ∂ z ) (\phi\partial/\partial x, \phi\partial/\partial y, \phi\partial/\partial z) (ϕ∂/∂x,ϕ∂/∂y,ϕ∂/∂z).
Examples
Example 1
Find the gradient of the scalar field ϕ = x y 2 z 3 \phi=xy^{2}z^{3} ϕ=xy2z3.
Solution
From the definition, the gradient of ϕ \phi ϕ is given by
∇ ϕ = i ∂ ϕ ∂ x + j ∂ ϕ ∂ y + k ∂ ϕ ∂ z = y 2 z 3 i + 2 x y z 3 j + 3 x y 2 z 2 k . \nabla \phi=\boldsymbol{i} \frac{\partial \phi}{\partial x}+\boldsymbol{j} \frac{\partial \phi}{\partial y}+\boldsymbol{k} \frac{\partial \phi}{\partial z}\\ =y^{2}z^{3}\boldsymbol{i}+2xyz^{3}\boldsymbol{j}+3xy^2z^2\boldsymbol{k}. ∇ϕ=i∂x∂ϕ+j∂y∂ϕ+k∂z∂ϕ=y2z3i+2xyz3j+3xy2z2k.
Geometrical properties
The gradient of a scalar field ϕ \phi ϕ has some interesting geometrical properties.
Let us first consider the problem of calculating the rate of change of ϕ \phi ϕ in some particular direction. For an infinitesimal vector displacement d r d\boldsymbol{r} dr, forming its scalar product with ∇ ϕ \nabla \phi ∇ϕ we obtain
∇ ϕ ⋅ d r = ( i ∂ ϕ ∂ x + j ∂ ϕ ∂ y + k ∂ ϕ ∂ z ) ⋅ ( i d x + j d y + k d z ) = ∂ ϕ ∂ x d x + ∂ ϕ ∂ y d y + ∂ ϕ ∂ z d z = d ϕ , \nabla \phi \cdot d\boldsymbol{r}=(\boldsymbol{i} \frac{\partial \phi}{\partial x}+\boldsymbol{j} \frac{\partial \phi}{\partial y}+\boldsymbol{k} \frac{\partial \phi}{\partial z}) \cdot (\boldsymbol{i}dx+\boldsymbol{j}dy+\boldsymbol{k}dz)\\ =\frac{\partial \phi}{\partial x}dx+\frac{\partial \phi}{\partial y}dy+\frac{\partial \phi}{\partial z}dz\\ =d\phi, ∇ϕ⋅dr=(i∂x∂ϕ+j∂y∂ϕ+k∂z∂ϕ)⋅(idx+jdy+kdz)=∂x∂ϕdx+∂y∂ϕdy+∂z∂ϕdz=dϕ,
which is the infinitesimal change in ϕ \phi ϕ in going from position r \boldsymbol{r} r to r + d r \boldsymbol{r}+d\boldsymbol{r} r+dr. In particular, if r \boldsymbol{r} r depends on some parameter u u u such that r ( u ) \boldsymbol{r}(u) r(u) defines a space curve then the total derivative of ϕ \phi ϕ with respect to u u u along the curve is simply
d ϕ d u = ∇ ϕ ⋅ d r d u . \frac{d\phi}{du}=\nabla \phi \cdot \frac{d\boldsymbol{r}}{du}. dudϕ=∇ϕ⋅dudr.
In the particular case where the parameter u u u is the arc length s along the curve, the total derivative of ϕ \phi ϕ with respect to s along the curve is given by
d ϕ d s = ∇ ϕ ⋅ t ^ , \frac{d\phi}{ds}=\nabla \phi \cdot \hat{\boldsymbol{t}}, dsdϕ=∇ϕ⋅t^,
where t ^ \hat{\boldsymbol{t}} t^ is the unit tangent to the curve at the given point.
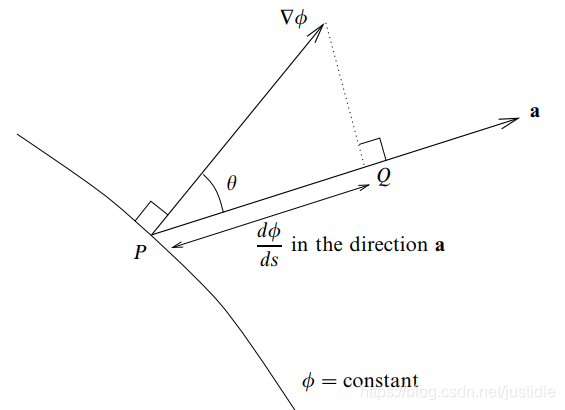
In general, the rate of change of ϕ \phi ϕ with respect to the distance s in a particular direction a \boldsymbol{a} a is given by
d ϕ d s = ∇ ϕ ⋅ a ^ \frac{d\phi}{ds}=\nabla \phi \cdot \hat{\boldsymbol{a}} dsdϕ=∇ϕ⋅a^
and is called the directional derivative. Since a ^ \hat{\boldsymbol{a}} a^ is a unit vector we have
d ϕ d s = ∣ ∇ ϕ ∣ c o s θ \frac{d\phi}{ds}=\lvert \nabla \phi \rvert cos\theta dsdϕ=∣∇ϕ∣cosθ
where θ \theta θ is the angle between a ^ \hat{\boldsymbol{a}} a^ and ∇ ϕ \nabla \phi ∇ϕ as shown in figure below. Clearly ∇ ϕ \nabla \phi ∇ϕ lies in the direction of the fastest increase in ϕ \phi ϕ, and ∣ ∇ ϕ ∣ \lvert \nabla \phi \rvert ∣∇ϕ∣ is the largest possible value of d ϕ / d s d\phi/ds dϕ/ds. Similarly, the largest rate of decrease of ϕ \phi ϕ is d ϕ / d s = − ∣ ∇ ϕ ∣ d\phi/ds=-\lvert \nabla \phi \rvert dϕ/ds=−∣∇ϕ∣ in the direction of − ∇ ϕ -\nabla \phi −∇ϕ.