动态规划-总结分析

❁声明：本文非完全原创性，其中参考资料摘自OI-WIKI：http://oi-wiki.com/dp/basic/，如有侵权，请联系我删除！

※三创/转载请注明原始作者、原始文章地址及本博客地址

☻文中如存在谬误、混淆等不足，欢迎批评指正！

动态规划应用于子问题重叠的情况：

1. 要去刻画最优解的结构特征；
2. 尝试递归地定义最优解的值（就是我们常说的考虑从 $i-1$ 转移到 $i$ ）；
3. 计算最优解；
4. 利用计算出的信息构造一个最优解。

动态规划的两种实现方法

1. 自顶向下法：记忆化搜索
2. 自底向上法(将问题按规模排序，类似于递推)

动态规划原理

动态规划要素：最优子结构、子问题重叠、重构最优解

最优子结构

具有最优子结构也可能是适合用贪心的方法求解。注意要确保我们考察了最优解中用到的所有子问题。

1. 证明问题最优解的第一个组成部分是做出一个选择；
2. 对于一个给定问题，在其可能的第一步选择中，你界定已经知道哪种选择才会得到最优解。你现在并不关心这种选择具体是如何得到的，只是假定已经知道了这种选择；
3. 给定可获得的最优解的选择后，确定这次选择会产生哪些子问题，以及如何最好地刻画子问题空间；
4. 证明作为构成原问题最优解的组成部分，每个子问题的解就是它本身的最优解。方法是反证法，考虑加入某个子问题的解不是其自身的最优解，那么就可以从原问题的解中用该子问题的最优解替换掉当前的非最优解，从而得到原问题的一个更优的解，从而与原问题最优解的假设矛盾。

要保持子问题空间尽量简单，只在必要时扩展。

最优子结构的不同体现在两个方面：

1. 原问题的最优解中涉及多少个子问题；
2. 确定最优解使用哪些子问题时，需要考察多少种选择。

子问题图中每个定点对应一个子问题，而需要考察的选择对应关联至子问题顶点的边。

经典问题：

• 无权最短路径： 具有最优子结构性质。
• 无权最长（简单）路径： 此问题不具有，是 NPC 的。区别在于，要保证子问题无关，即同一个原问题的一个子问题的解不影响另一个子问题的解。相关：求解一个子问题时用到了某些资源，导致这些资源在求解其他子问题时不可用。

子问题重叠

子问题空间要足够小，即问题的递归算法会反复地求解相同的子问题，而不是一直生成新的子问题。

重构最优解

存表记录最优分割的位置，就不用重新按照代价来重构。

闫氏DP分析法

总结自UP主：大雪菜(yxc)大佬(ACWing创始人)

核心思想：从集合的角度去分析DP问题

1.状态表示：用维度数组$dp[i]$表示(维度根据题目来定)

• 集合：$dp[i][j]$：$dp$数组的含义：确定状态下的$dp[i][j]$,即满足约束条件下的解的集合，其值为属性的具体化

  通过寻找最后一个状态不同的点确定划分的方法

• 属性：集合内解的特性-最大值max、最小值min、集合元素的个数。

  注意：$dp$数组维护的是集合某种特性的值！

2.状态计算：即化整为零的过程。将大集合分成若干个子集，再通过子集地推出末状态

一般分析步骤：

1. 先根据题意确定dp数组的含义，再根据题目的诉求确定dp数组维护的特性
2. 分析出集合的划分方法（通过寻找最后一个状态不同的点确定划分的方法），得到递推方程
3. 确定初始化状态$dp[1]=？$
4. 敲键盘

dp问题的下标

1. 若状态转移方程中有$f[i-1]$这种状态, 下标(状态转移那部分代码)尽量从1开始
2. 否则就最好从0开始

dp问题的时间复杂度
状态数量(n^几个约束维度) * 转移状态的时间复杂(状态转移代码的时间复杂度)

dp的集合划分依据 -> 寻找最后一个不同操作. 加不加这个背包, 数字三角形最后一步是由左边还是右边走过来的呀(根据操作的不同来对集合进行划分)
使得划分之后的小集合可以递推求出当前集合, 且最小集合已知

注意：集合的划分一定要不漏，不一定不重！

动态规划-分类

1.简单DP-序列处理问题

1.1.最长公共子序列

子序列允许不连续。每个 $c[i][j]$ 只依赖于 $c[i-1][j]$ 、 $c[i][j-1]$ 和 $c[i-1][j-1]$ 。

记录最优方案的时候可以不需要额外建表（优化空间），因为重新选择一遍（转移过程）也是 $O(1)$ 的。

模板算法

ios::sync_with_stdio(false);
string a, b; cin >> a >> b;
int dp[MAX];
for(int i = 0; i < a.length(); i++){
    
    
    for(int j = 0; j < b.length(); j++){
    
    
        if(a[i] == a[j]) dp[i + 1][j + 1] = dp[i][j] + 1;
        else dp[i + 1][j + 1] = max(dp[i + 1][j], fp[i][j + 1]);
    }
}
cout << dp[a.lenght()][b.length()] << endl;

1.2.最长连续上升子序列(不下降)

模板算法

int a[MAXN];
int dp(){
    
    
    int now = 1, ans = 1;
    for(int i = 2; i <= n; i++){
    
    
        if(a[i] >= a[i - 1]) now++;
        else now = 1
        ans = ans > now ? ans : now;
    }
}

1.3.最长上升子序列(不下降)

模板算法1：O(n²)

int a[MAXN], b[MAXN], dp[MAXN];
int dp(){
    
    
    dp[1] = 1;
    int ans = 1;
    for(int i = 2; i <= n; i++){
    
    
        for(int j = 1; j < i; j++){
    
    
            if(a[j] >= a[i]){
    
    
                dp[i] = max(dp[i], dp[j] + 1);
                ans = max(ans, dp[i]);
            }
        }
    }
    return ans;
}

模板算法2：0(n logn)

$O\left(n\log n\right)$ 的算法，参考了这篇文章 https://www.cnblogs.com/itlqs/p/5743114.html 。

首先，定义 $a_1\dots a_n$ 为原始序列， $d$ 为当前的不下降子序列， $len$ 为子序列的长度，那么 $d_{len}$ 就是长度为 $len$ 的不下降子序列末尾元素。

初始化： $d_1=a_1,len=1$ 。

现在我们已知最长的不下降子序列长度为 1，那么我们让 $i$ 从 2 到 $n$ 循环，依次求出前 $i$ 个元素的最长不下降子序列的长度，循环的时候我们只需要维护好 $d$ 这个数组还有 $len$ 就可以了。 关键在于如何维护。

考虑进来一个元素 $a_i$ ：

1. 元素大于 $d_{len}$ ，直接 $d_{++len}=a_i$ 即可，这个比较好理解。
2. 元素等于 $d_{len}$ ，因为前面的元素都小于它，所以这个元素可以直接抛弃。
3. 元素小于 $d_{len}$ ，找到 第一个 大于它的元素，插入进去，其他小于它的元素不要。

for (int i = 0; i < n; ++i) scanf("%d", a + i);
memset(dp, 0x1f, sizeof dp);
mx = dp[0];
for (int i = 0; i < n; ++i) {
    
    
  *std::upper_bound(dp, dp + n, a[i]) = a[i];
}
ans = 0;
while (dp[ans] != mx) ++ans;

2.背包DP-背包类问题总结-全

参考自：背包问题九讲、OI-WIKI

2.1 0-1背包

设 DP 状态 $f_{i,j}$ 为在只能放前 $i$ 个物品的情况下，容量为 $j$ 的背包所能达到的最大总价值。

考虑转移。假设当前已经处理好了前 $i-1$ 个物品的所有状态，那么对于第 $i$ 个物品，当其不放入背包时，背包的剩余容量不变，背包中物品的总价值也不变，故这种情况的最大价值为 $f_{i-1,j}$ ；当其放入背包时，背包的剩余容量会减小 $w_i$ ，背包中物品的总价值会增大 $v_i$ ，故这种情况的最大价值为 $f_{i-1,j-w_i}+v_i$ 。

由此可以得出状态转移方程：

$$f_{i,j}=\max (f_{i-1,j},f_{i-1,j-w_i}+v_i)$$

这里如果直接采用二维数组对状态进行记录，会出现 MLE。可以考虑改用滚动数组的形式来优化。

由于对 $f_i$ 有影响的只有 $f_{i-1}$ ，可以去掉第一维，直接用 $f_i$ 来表示处理到当前物品时背包容量为 $i$ 的最大价值，得出以下方程：

$$f_j=\max \left(f_j,f_{j-w_i}+v_i\right)$$

0-1背包模板：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10, M = 1e7 + 10;
int w[N], v[N], dp[M];

int main(){
    
    
	int n, m; cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> w[i] >> v[i];
    for(int i = 1; i <= n; i++){
    
    
        for(int j = m; j >= w[i]; j--){
    
    
            dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
        }
    }
	cout << dp[m] << endl;
	return 0;
}

注意：0-1背包需要倒序扫描/枚举，当正序枚举时：对于当前处理的物品 $i$ 和当前状态 $f_{i,j}$ ，在 $j⩾w_i$ 时， $f_{i,j}$ 是会被 $f_{i,j-w_i}$ 所影响的。这就相当于物品 $i$ 可以多次被放入背包，与题意不符。（事实上，这正是完全背包问题的解法）为了避免这种情况发生，我们可以改变枚举的顺序，从 $W$ 枚举到 $w_i$ ，这样就不会出现上述的错误，因为 $f_{i,j}$ 总是在 $f_{i,j-w_i}$ 前被更新。

2.2 完全背包问题

区别于0-1背包问题，完全背包问题对于物品数量的选取有所不同，0-1背包中的”0-1”表示每个物品只会存在选中和未选中两种状态(0和1状态)，而完全背包则是对于每种物品具有多种状态，即通俗意义上的可重复选取，即为无穷选取状态。

类似的，我们可以借鉴0-1背包的思路，设 $f_{i,j}$ 为只能选前 $i$ 个物品时，容量为 $j$ 的背包可以达到的最大价值。对于第 $i$ 件物品，枚举其选了多少个来转移。这样做的时间复杂度是 $O(n^3)$ 的。状态转移方程如下：
$$f_{i,j}=\underset{k=0}{\overset{+\infty }{\max }}(f_{i-1,j-k\times w_i}+v_i\times k)$$
状态转移方程如下：
$$f_{i,j}=\max (f_{i-1,j},f_{i,j-w_i}+v_i)$$
解释：对于 $f_{i,j}$ ，只要通过 $f_{i,j-w_i}$ 转移就可以。当我们这样转移时， $f_{i,j-w_i}$ 已经由 $f_{i,j-2\times w_i}$ 更新过，那么 $f_{i,j-w_i}$ 就是充分考虑了第 $i$ 件物品所选次数后得到的最优结果。换言之，我们通过局部最优子结构的性质重复使用了之前的枚举过程，优化了枚举的复杂度。

在0-1背包中我们已经讨论过，二维的数组表示法会产生巨大的空间开销而导致MLE，因此我们可以运用0-1背包中的结论，利用滚动数组对完全背包问题进行优化：

完全背包模板

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10, M = 1e7 + 10;
int w[N], v[N], dp[M];

int main(){
    
    
    int n, m; cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> w[i] >> v[i];
    for(int i = 1; i <= n; i++){
    
    
        for(int j = w[i]; j <= m; j++){
    
    
            dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
        }
    }
    cout << dp[m] << endl;
    return 0;
}

2.3 多重背包

多重背包是 0-1 背包的一个变式。也是完全背包的限定状态，与 0-1 背包的区别在于每种物品 y 有 $k_i$ 个，而非 $1$ 个，与完全背包的状态差异为无限物品和有限物品的区别。

对于多重背包问题，我们可以将其转换为0-1背包问题进行求解：把「每种物品选 $k_i$ 次」等价转换为「有 $k_i$ 个相同的物品，每个物品选一次」。这样就转换成了一个 0-1 背包模型，套用上文所述的方法就可已解决。状态转移方程如下：

$$f_{i,j}=\underset{k=0}{\overset{k_i}{\max }}(f_{i-1,j-k\times w_i}+v_i\times k)$$

时间复杂度 $O(W{\sum }_{i=1}^n{k}_i)$ 。

朴素算法：直接转化为0-1背包问题求解的多重背包模板：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10, M = 1e7 + 10;
int v[N], w[N], dp[M];

int main(){
    
    
    int n, m, flag = 0; cin >> n >> m;
    while(n--){
    
    
        int value, weight, numm;
        cin >> weight >> value >> numm;
        while(numm--) v[++flag] = value, w[flag] = weight;
    }
    for(int i = 1; i <= flag; i++){
    
    
        for(int j = m; j >= w[i]; j--){
    
    
            dp[j] = max(dp[j - w[i]] + v[i], dp[j]);
        }
    }
    cout << dp[m] << endl;
    return 0;
}

2.4 多重背包-二进制优化

在朴素算法解决多重背包中，我们注意到所谓的“多重背包”被展开成为0-1背包问题求解，每件商品都要根据其数量进行展开，显然这样会造成大量的空间开销(甚至MLE)，因此我们需要考虑对算法进行优化。

在对多重背包的算法进行优化时，我们仍然继续考虑转换为0-1背包求解，显然，复杂度中的 $O(nW)$ 部分无法再优化了，我们只能从 $O(\sum k_i)$ 处入手。为了表述方便，我们用 $A_{i,j}$ 代表第 $i$ 种物品拆分出的第 $j$ 个物品。

在朴素的做法中， $\forall j\le k_i$ ， $A_{i,j}$ 均表示相同物品。那么我们效率低的原因主要在于我们进行了大量重复性的工作。举例来说，我们考虑了「同时选 $A_{i,1},A_{i,2}$ 」与「同时选 $A_{i,2},A_{i,3}$ 」这两个完全等效的情况。这样的重复性工作我们进行了许多次。那么优化拆分方式就成为了解决问题的突破口。

我们可以通过「二进制分组」的方式使拆分方式更加优美。

具体地说就是令 $A_{i,j}\left(j\in \left[0,\lfloor {\log }_2(k_i+1)\rfloor -1\right]\right)$ 分别表示由 $2^j$ 个单个物品「捆绑」而成的大物品。特殊地，若 $k_i+1$ 不是 $2$ 的整数次幂，则需要在最后添加一个由 $k_i-2^{\lfloor {\log }_2(k_i+1)\rfloor -1}$ 个单个物品「捆绑」而成的大物品用于补足。

举几个例子：

• $6=1+2+3$
• $8=1+2+4+1$
• $18=1+2+4+8+3$
• $31=1+2+4+8+16$

显然，通过上述拆分方式，可以表示任意 $\le k_i$ 个物品的等效选择方式。将每种物品按照上述方式拆分后，使用 0-1 背包的方法解决即可。

优化后的时间复杂度 $O(W{\sum }_{i=1}^n{\log }_2{k}_i)$

多重背包：二进制优化模板：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10, M = 1e8 + 10;
int w[N], v[N];
int dp[M];

int main(){
    
    
    int n, m, ind = 0; cin >> n >> m;
    //分组操作
    for(int i = 1; i <= n; i++){
    
    
        int c = 1, weight, value, num;
        cin >> weight >> value >> num;
        while(num - c > 0){
    
    
            num -= c;
            w[++ind] = weight * c;
            v[ind] = value * c;
            c *= 2;
        }
        w[++ind] = weight * num;
        v[ind] = value * num;
    }
    //0-1背包模板
    for(int i = 1; i <= ind; i++){
    
    
        for(int j = m; j >= w[i]; j--){
    
    
            dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
        }
    }
    cout << dp[m] << endl;
    return 0;
}

2.5 混合背包

混合背包即：将0-1背包、完全背包、多重背包混合在一起构成的的问题，解决的方南很简单，分别对不同的物品类别采取不同的措施即可。

混合背包伪代码描述：

for (循环物品种类) {
    
    
  if (是 0 - 1 背包)
    套用 0 - 1 背包代码;
  else if (是完全背包)
    套用完全背包代码;
  else if (是多重背包)
    套用多重背包代码;
}

2.6 二维费用背包

二维费用背包问题是0-1背包问题的扩展，与0-1背包不同的是，每个物品具有两个(甚至更多)的权重，在选择的过程中消耗的背包空间比单纯的0-1背包多一个维度。

对于二维费用背包问题，我们通常采取增加循环层数、dp数组加维度解决

二维费用背包模板：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
int w1[N], w2[N], v[N], dp[N][N];

int main(){
    
    
    int n, m, t; cin >> n >> m >> t;
    for(int i = 1; i <= n; i++) cin >> w1[i] >> w2[i] >> v[i];

    for(int i = 1; i <= n; i++){
    
    
        for(int j = m; j >= w1[i]; j--){
    
    
            for(int k = t; k >= w2[i]; k--){
    
    
                dp[j][k] = max(dp[j - w1[i]][k - w2[i]] + v[i], dp[j][k]);
            }
        }
    }
    cout << dp[m][t] << endl;
    return 0;
}

2.7 分组背包问题

顾名思义，分组背包即将物品分成不同的组放入背包，不同的组之间相互冲突，只能选择一件放入

解决分组背包问题的思想仍是转化为0-1背包模型求解，分组背包即是将0-1背包中的在每组中选择一件改为了在当前组中选择一件，因此我们只需要对每一组分别跑一次0-1背包即可。

我们可以将 $t_{k,i}$ 表示第 $k$ 组的第 $i$ 件物品的编号是多少，再用 $cn{t}_k$ 表示第 $k$ 组物品有多少个。

分组背包模板：

#include <bits/stdc++.h>
using namespace std;
const int M = 1010, N = 1010;
int dp[M], w[N], v[N], t[101][20], cnt[101], cn;
int main()
{
    
    
    int n, m; cin >> n >> m;
    for (int i = 1; i <= n; i++){
    
    
        int C; cin >> w[i] >> v[i] >> C;
        cn = max(cn, C); //cn记录共有几组
        cnt[C]++;         //cnt[]记录第C组共有几件物品
        t[C][cnt[C]] = i; //t[][]记录第C组第i件物品的的序号
    }
    for (int i = 1; i <= cn; i++)            //枚举cn个组
        for (int j = m; j >= 0; j--)         //枚举容量
            for (int k = 1; k <= cnt[i]; k++) //枚举各组中物品的序号
                if (j >= w[t[i][k]]) dp[j] = max(dp[j], dp[j - w[t[i][k]]] + v[t[i][k]]); //套用状态转移方程
    cout << dp[m] << endl;
    return 0; 
}

2.8 有依赖的背包问题/条件背包问题

这类问题的鲜明特征是，当选择第如果选第 $i$ 件物品，就必须选第 $j$ 件物品，且保证不会循环引用，一部分题目甚至会出现多叉树的引用形式。

一般的，将无依赖条件的物品称为“主件”，有依赖条件的物品成为“附件”。

对于包含一个主件和若干个附件的集合有以下可能性：仅选择主件，选择主件后再选择一个附件，选择主件后再选择两个附件……需要将以上可能性的容量和价值转换成一件件物品。因为这几种可能性只能选一种，所以可以将这看成分组背包。

！如果是多叉树的集合，则要先算子节点的集合，最后算父节点的集合。

有依赖的背包问题模板：

#待补充

2.9 泛化物品的背包问题

对于这类背包问题，没有固定的费用和价值，它的价值是随着分配给它的费用而定。在背包容量为 $V$ 的背包问题中，当分配给它的费用为 $v_i$ 时，能得到的价值就是 $h\left(v_i\right)$ 。这时，将固定的价值换成函数的引用即可。

相较于0-1背包，这种背包问题的状态转移方程中嵌套有价值计算函数，其余依然与0-1背包保持一致。

背包问题附属问题

2.9.1背包-优化

根据贪心原理，当费用相同时，只需保留价值最高的；当价值一定时，只需保留费用最低的；当有两件物品 $i,j$ 且 $i$ 的价值大于 $j$ 的价值并且 $i$ 的费用小于 $j$ 的费用是，只需保留 $j$ 。

2.9.2输出方案

输出方案其实就是记录下来背包中的某一个状态是怎么推出来的。我们可以用 $g_{i,v}$ 表示第 $i$ 件物品占用空间为 $v$ 的时候是否选择了此物品。然后在转移时记录是选用了哪一种策略（选或不选）。输出时的伪代码：

int v = V;  // 记录当前的存储空间
for (
    从最后一件循环至第一件)  // 因为最后一件物品存储的是最终状态，所以从最后一件物品进行循环
{
    
    
  if (g[i][v]) {
    
    
    选了第 i 项物品;
    v -= 第 i 项物品的价值;
  } else
    未选第 i 项物品;
}

2.9.3求方案数

对于给定的一个背包容量、物品费用、其他关系等的问题，求装到一定容量的方案总数。

这种问题就是把求最大值换成求和即可。

例如 0-1 背包问题的转移方程就变成了：

$$d{p}_i=\sum (d{p}_i,d{p}_{i-c_i})$$

初始条件： $d{p}_0=1$

因为当容量为 $0$ 时也有一个方案：什么都不装！

2.9.4求最优方案总数

要求最优方案总数，我们要对 0-1 背包里的 dp 数组的定义稍作修改，DP 状态 $f_{i,j}$ 为在只能放前 $i$ 个物品的情况下，容量为 $j$ 的背包“正好装满”所能达到的最大总价值。

这样修改之后，每一种 DP 状态都可以用一个 $g_{i,j}$ 来表示方案数。

$f_{i,j}$ 表示只考虑前 $i$ 个物品时背包体积“正好”是 $j$ 时的最大价值。

$g_{i,j}$ 表示只考虑前 $i$ 个物品时背包体积“正好”是 $j$ 时的方案数。

转移方程：

如果 $f_{i,j}==f_{i-1,j}且f_{i,j}!=f_{i-1,j-v}+w$ 说明我们此时不选择把物品放入背包更优，方案数由 $g_{i-1,j} 转移过来，

如果 $f_{i,j}!=f_{i-1,j}且f_{i,j}==f_{i-1,j-v}+w$ 说明我们此时选择把物品放入背包更优，方案数由 $g_{i-1,j-v} 转移过来，

如果 $f_{i,j}==f_{i-1,j}且f_{i,j}==f_{i-1,j-v}+w$ 说明放入或不放入都能取得最优解，方案数由 $g_{i-1,j}和$ g_{i-1,j-v} 转移过来。

初始条件：

memset(f, 0x3f3f, sizeof(f))  // 避免没有装满而进行了转移
f[0] = 0;
g[0] = 1;  // 什么都不装是一种方案

因为背包体积最大值有可能装不满，所以最优解不一定是 $f_m$ 。

最后我们通过找到最优解的价值，把 $g_j$ 数组里取到最优解的所有方案数相加即可。

核心代码：

for (int i = 0; i < N; i++) {
    
    
  for (int j = V; j >= v[i]; j--) {
    
    
    int tmp = max(dp[j], dp[j - v[i]] + w[i]);
    int c = 0;
    if (tmp == dp[j]) c += cnt[j];                       // 如果从dp[j]转移
    if (tmp == dp[j - v[i]] + w[i]) c += cnt[j - v[i]];  // 如果从dp[j-v[i]]转移
    dp[j] = tmp;
    cnt[j] = c;
  }
}
int max = 0;  // 寻找最优解
for (int i = 0; i <= V; i++) {
    
    
  max = max(max, dp[i]);
}
int res = 0;
for (int i = 0; i <= V; i++) {
    
    
  if (dp[i] == max) {
    
    
    res += cnt[i];  // 求和最优解方案数
  }
}

3.区间DP

区间DP：区间类动态规划是线性动态规划的扩展，它在分阶段地划分问题时，与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来由很大的关系。令状态 $f(i,j)$ 表示将下标位置 $i$ 到 $j$ 的所有元素合并能获得的价值的最大值，那么 f ( i , j ) = max ⁡ { f ( i , k ) + f ( k + 1 , j ) + c o s t } f(i,j)=\max\{f(i,k)+f(k+1,j)+cost\} f(i,j)=max{ f(i,k)+f(k+1,j)+cost} ， $cost$ 为将这两组元素合并起来的代价。

区间DP的特征：

• 合并 ：即将两个或多个部分进行整合，当然也可以反过来；

• 特征 ：能将问题分解为能两两合并的形式；

• 求解 ：对整个问题设最优值，枚举合并点，将问题分解为左右两个部分，最后合并两个部分的最优值得到原问题的最优值。

for(int len = 1;len<=n;len++){
    
                        //枚举长度
        for(int i = 1; i + len <= n + 1; i++){
    
        //枚举起点，ends<=n
            int ends = i + len - 1;				  //区间终点计算
            for(int j = i; j < ends; j++){
    
            //枚举区间间断点，更新每个小区间的最小值
                dp[i][ends] = min(dp[i][ends], dp[i][j] + dp[j + 1][ends] + new_value);	//dp[区间的最小值] = max/min(历史值， 新合并方案下的值)
        }
    }

典型区间DP：链形区间DP、环形区间DP

链形区间DP模板

模板背景：$N$堆石子排成一列，首尾不想接，.规定每次只能选相邻的$2$堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出一个算法,计算出将 $N $堆石子合并成 $1$ 堆的最小得分和最大得分。

令 $f(i,j)$ 表示将区间 $[i,j]$ 内的所有石子合并到一起的最大得分。

写出 状态转移方程 ： f ( i , j ) = m a x { f ( i , k ) + f ( k + 1 , j ) + ∑ t = i j a t }   ( i ≤ k < j ) f(i,j)=max\{f(i,k)+f(k+1,j)+\sum_{t=i}^{j} a_t \}~(i\le k<j) f(i,j)=max{ f(i,k)+f(k+1,j)+∑t=ij​at​} (i≤k<j)

令 $su{m}_i$ 表示 $a$ 数组的前缀和，状态转移方程变形为 f ( i , j ) = m a x { f ( i , k ) + f ( k + 1 , j ) + s u m j − s u m i − 1 } f(i,j)=max\{f(i,k)+f(k+1,j)+sum_j-sum_{i-1} \} f(i,j)=max{ f(i,k)+f(k+1,j)+sumj​−sumi−1​} 。

进行状态转移的方法：

由于计算 $f(i,j)$ 的值时需要知道所有 $f(i,k)$ 和 $f(k+1,j)$ 的值，而这两个中包含的元素的数量都小于 $f(i,j)$ ，所以我们以 $len=j-i+1$ 作为 DP 的阶段。首先从小到大枚举 $len$ ，然后枚举 $i$ 的值，根据 $len$ 和 $i$ 用公式计算出 $j$ 的值，然后枚举 $k$ ，时间复杂度为 $O(n^3)$

#include <bits/stdc++.h>
using namespace std;
int stone[105], dp[205][205], sum[105];

int main(){
    
    
    int n = 0; cin >> n;
    memset(sum, 0, sizeof(sum));
    for(int i = 0; i < 205; i++)
        for(int j = 0; j < 205; j++) dp[i][j] = INT_MAX;
    for(int i = 1; i <= n; i++){
    
    
        cin >> stone[i];
        sum[i] = sum[i - 1] + stone[i], dp[i][i] = 0;
    }
    for(int len = 1; len <= n; len++){
    
    
        for(int i = 1; i + len <= n + 1; i++){
    
    
            int ends = i + len - 1;
            for(int j = i; j < ends; j++){
    
    
                dp[i][ends] = min(dp[i][ends], dp[i][j] + dp[j + 1][ends] + sum[ends] - sum[i - 1]);
            }
        }
    }
    cout << dp[1][n] << endl;
    return 0;
}

环形区间DP模板

模板背景：在一个圆形操场的四周摆放 $N$ 堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的$2$堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出一个算法,计算出将 $N $堆石子合并成 $1$ 堆的最小得分和最大得分。

方法一 ：由于石子围成一个环，我们可以枚举分开的位置，将这个环转化成一个链，由于要枚举 $n$ 次，最终的时间复杂度为 $O(n^4)$ 。

方法二 ：我们将这条链延长两倍，变成 $2\times n$ 堆，其中第 $i$ 堆与第 $n+i$ 堆相同，用动态规划求解后，取 $f(1,n),f(2,n+1),...,f(i,n+i-1)$ 中的最优值，即为最后的答案。时间复杂度 $O(n^3)$

#include <bits/stdc++.h>
using namespace std;
int stone[105], dpmin[205][205], dpmax[205][205], sum[205];
int main()
{
    
    
    int n = 0; cin >> n;
    memset(sum, 0, sizeof(sum));
    for(int i = 0; i <= 205; i++){
    
    
        for(int j = 0; j <= 205; j++){
    
    
            dpmin[i][j] = INT_MAX;
            dpmax[i][j] = INT_MIN;
        }
    }
    for(int i = 1; i <= n; i++){
    
    
        cin >> stone[i];
        sum[i] = sum[i - 1] + stone[i];
        dpmin[i][i] = 0;
        dpmax[i][i] = 0;
    }
    for(int i = 1; i <= n; i++){
    
    
        sum[i + n] = sum[i + n - 1] + stone[i];
        dpmin[i + n][i + n] = 0;
        dpmax[i + n][i + n] = 0;
    }
    for(int len = 1; len <= n; len++){
    
    
        for(int i = 1; i + len <= 2 * n; i++){
    
    
            int ends = i + len - 1;
            for(int j = i; j < ends; j++){
    
    
                dpmin[i][ends] = min (dpmin[i][ends], dpmin[i][j] + dpmin[j + 1][ends] + sum[ends] - sum[i - 1]);
                dpmax[i][ends] = max (dpmax[i][ends], dpmax[i][j] + dpmax[j + 1][ends] + sum[ends] - sum[i - 1]);
            }
        }
    }
    int ansmin = INT_MAX;
    int ansmax = INT_MIN;
    for(int i = 1;i <= n; i++){
    
    
        ansmin = min(ansmin, dpmin[i][i + n - 1]);
        ansmax = max(ansmax, dpmax[i][i + n - 1]);
    }
    cout << ansmin << endl;
    cout << ansmax << endl;
    return 0;
}

四边形不等式优化法(待补齐)：

优化核心思想：保存最优分割点，在查找过程中用保存的最优分割点优化查找过程

实现方法：见DP优化方案-四边形不等式优化法

4.DAG-DP(有向无环图DP)

许多问题中刻画的二元关系，实际可以通过DAG来建模，通过DP解决

例题：巴比伦塔

有 $n(n⩽30)$ 种砖块，已知三条边长，每种都有无穷多个。要求选一些立方体摞成一根尽量高的柱子（每个砖块可以自行选择一条边作为高），使得每个砖块的底面长宽分别严格小于它下方砖块的底面长宽，求塔的最大高度。

(洛谷传送门：UVA437 巴比伦塔)

DAG-DP：题目分析：

1. 建立DAG

   由于每个砖块的底面长宽分别严格小于它下方砖块的底面长宽，因此不难将这样一种关系作为建图的依据，而本题也就转化为最长路问题。

   也就是说如果砖块 $j$ 能放在砖块 $i$ 上，那么 $i$ 和 $j$ 之间存在一条边 $(i,j)$ ，且边权就是砖块 $j$ 所选取的高。

   本题的另一个问题在于每个砖块的高有三种选法，怎样建图更合适呢？

   不妨将每个砖块拆解为三种堆叠方式，即将一个砖块分解为三个砖块，每一个拆解得到的砖块都选取不同的高。

   初始的起点是大地，大地的底面是无穷大的，则大地可达任意砖块，当然我们写程序时不必特意写上无穷大。

2. 状态转移

   题目要求的是塔的最大高度，已经转化为最长路问题，其起点上文已指出是大地，那么终点呢？

   显然终点已经自然确定，那就是某砖块上不能再搭别的砖块的时候。

   之前在图上标记的黄虚框表明有重复计算，下面我们开始考虑转移方程。

   显然，砖块一旦选取了高，那么这块砖块上最大能放的高度是确定的。

   某个砖块 $i$ 有三种堆叠方式分别记为 $0,1,2$ ，那么对于砖块 $i$ 和其堆叠方式 $r$ 来说则有如下转移方程

   d ( i , r ) = max ⁡ { d ( j , r ′ ) + h ′ } d(i, r) = \max\left\{d(j, r') + h'\right\} d(i,r)=max{ d(j,r′)+h′}

   其中 $j$ 是所有那些在砖块 $i$ 以 $r$ 方式堆叠时可放上的砖块， $r^{\prime }$ 对应 $j$ 此时的摆放方式，也就确定了此时唯一的高度 $h^{\prime }$ 。

   在实际编写时，将所有 $d(i,r)$ 都初始化为 $-1$ ，表示未计算过。

   在试图计算前，如果发现已经计算过，直接返回保存的值；否则就按步计算，并保存。

   最终答案是所有 $d(i,r)$ 的最大值。

#include<bits/stdc++.h>
using namespace std;
const int N = 40, M = 1000;
int x[N], y[N], z[N], dp[M][M];

int brick_sub(int c, int rot, int n){
    
    
    if(dp[c][rot] != -1) return dp[c][rot];
    dp[c][rot] = 0;
    int base1, base2;
    if(rot == 0) base1 = x[c], base2 = y[c];
    if(rot == 1) base1 = y[c], base2 = z[c];
    if(rot == 2) base1 = x[c], base2 = z[c];
    for(int i = 1; i <= n; i++){
    
    
        if ((x[i] < base1 && y[i] < base2) || (y[i] < base1 && x[i] < base2))
            dp[c][rot] = max(dp[c][rot], brick_sub(i, 0, n) + z[i]);
        if ((y[i] < base1 && z[i] < base2) || (z[i] < base1 && y[i] < base2))
            dp[c][rot] = max(dp[c][rot], brick_sub(i, 1, n) + x[i]);
        if ((x[i] < base1 && z[i] < base2) || (z[i] < base1 && x[i] < base2))
            dp[c][rot] = max(dp[c][rot], brick_sub(i, 2, n) + y[i]);
    }
    return dp[c][rot];
}

int brick(int n){
    
    
    for(int i = 1; i <= n; i++) dp[i][0] = dp[i][1] = dp[i][2] = -1;
    int r = 0;
    for(int i = 1; i <= n; i++){
    
    
        r = max(r, brick_sub(i, 0, n) + z[i]);
        r = max(r, brick_sub(i, 1, n) + x[i]);
        r = max(r, brick_sub(i, 2, n) + y[i]);
    }
    return r;
}

int main(){
    
    
    int caseser = 0;
    while(true){
    
    
        int n = 0; cin >> n;
        if(!n) return 0; else caseser++;
        for(int i = 1; i <= n; i++) cin >> x[i] >> y[i] >> z[i];
        cout << "Case " << caseser << ":" << " maximum height = " << brick(n);
    }
    return 0;
}

5.树形DP

别问为什么空着，，，我还不会啊。。。

6.状压DP

状压DP通过将状态压缩为整数来达到优化转移的目的。

我们通过几个例题来分析状压DP的思维过程

例题1：互不侵犯-典型状压DP

个人题解博客：互不侵犯-状压DP分析

在 $N\times N$ 的棋盘里面放 $K$ 个国王，使他们互不攻击，共有多少种摆放方案。国王能攻击到它上下左右，以及左上左下右上右下八个方向上附近的各一个格子，共 $8$ 个格子。

---

下面对状压的过程进行详细的分析：首先什么是状压：

状压-即通过将状态压缩为整数来达到优化转移的目的。

对于本题，我们可以用一个二维数组来储存图，数组的对应位置表示棋盘上的实际位置，这事的状态并未进行压缩。

由于N的范围较小$(N<=9)$，我们可以很自然的反映出来：我们可以用二进制整数来表示每一行的状态，如图所示：

在上述的行状态下，我们通过一个八位二进制整数来表示了一行中各个位置的状态：10101010

既然这种方式成立，那么我们就可以根据二进制数各位表示的状态进行状态转移

了解了何为状压，接下来就是DP的分析

我们采用闫氏DP分析法进行分析：

状态转移方程的推导

首先，假设在第i-1行的的第j列放置一枚棋子，那么如图所示，第j行会出现不合法放置位置

即：第i行的$$j-1,j,j+1$$位置是非法的，那么在状压后如何对这些非法状态进行检测呢？相信你一定会立即反应出来：二进制运算

对于$j$位置的棋子，我们通过直接进行与运算进行检测，如果为1证明状态非法；

对于$j-1$位置的棋子，我们通过对L1左移进行检测(也可以对L2进行右移，原理相同)，如果为1证明状态非法；

对于$j+1$位置的棋子，我们通过对L1右移进行检测(也可以对L2进行左移，原理相同)，如果为1证明状态非法；

我们可以总结：当L2由L1进行转移时，必须满足的条件是：

(L2 & L1 == 0) && ((L2 << 1) & L1 == 0) && ((L2 >> 1) & L1 == 0)

化简得：

((L2|(L2 >> 1)|(L2 << 1)) & L1 == 0)

同时，第$i-1$行的$j-1,j+1$位置也是非法的，我们同样可以通过移位与运算进行检验：

合法的状态：

非法的状态：

满足条件：

((L << 1) | (L >> 1)) & L == 0

由于我们向下扫描递推，因此自上向下诞生合法状态，无需在考虑上一行是否合法。因此，下一步L2满足的状态我们全部总结完毕

因为第二个条件只与状态的情况有关，所以我们可以预处理这个东西，跑DP的时候将所有满足第二条性质的状态拿出来看看是否再满足第一条性质就好了；

设当前行的状态为 $j$ ，上一行的状态为 $x$ ，可以得到下面的转移方程： $f(i,j,l)=\sum f(i-1,x,l-sta(x))$ 。

#include <bits/stdc++.h>
using namespace std;
long long sta[2005], sit[2005], f[15][2005][105];
int n, k, cnt = 0;
void dfs(int x, int num, int cur)
{
    
    
    if (cur >= n){
    
     // 有新的合法状态
        sit[++cnt] = x;
        sta[cnt] = num;
        return;
    }
    dfs(x, num, cur + 1); // cur位置不放国王
    dfs(x + (1 << cur), num + 1, cur + 2); // cur位置放国王，与它相邻的位置不能再放国王
}
int main()
{
    
    
    cin >> n >> k;
    dfs(0, 0, 0); // 先预处理一行的所有合法状态
    for (int i = 1; i <= cnt; i++)
        f[1][i][sta[i]] = 1;
    for (int i = 2; i <= n; i++)
        for (int j = 1; j <= cnt; j++)
            for (int l = 1; l <= cnt; l++){
    
    
                if (sit[j] & sit[l]) continue;
                if ((sit[j] << 1) & sit[l]) continue;
                if (sit[j] & (sit[l] << 1)) continue;
                // 排除不合法转移
                for (int p = sta[j]; p <= k; p++) f[i][j][p] += f[i - 1][l][p - sta[j]];
            }
    long long ans = 0;
    for (int i = 1; i <= cnt; i++) ans += f[n][i][k]; // 累加答案
    cout << ans << endl;
    return 0;
}

7.数位DP

数位 DP 问题往往都是这样的题型，给定一个闭区间 $[l,r]$ ，让你求这个区间中满足 某种条件(性质) 的数的总数。

例题： Windy数：给定一个区间 $[l,r]$ ，求其中满足条件 **不含前导 $0$ 且相邻两个数字相差至少为 $2$ ** 的数字个数。

数位DP的思路：

1.区间转化

想要求出$[a,b]$内的windy数个数，需要先求出$[0,x]$的windy数的个数。

最后的答案即为：$dp[b]-dp[a-1]$

2.数位填数

设整数x一共n位，x表示为$a_n{a}_{n-1}{a}_{n-2}...a_1$,从高位到低位进行枚举填数。因为要求不含前导0，因此最高位只能填$1～a_n$, 其他位可以填$0～a_i$。

每个位上填数的时候，为了保证不超过x，因此可以分为两类: $0～a_{i-1}$和$a_i$

3.状态转移方程

令$f[i][j]$表示一共有i位，且最高位数字为$j$的$windy$数​的个数

我们对数位采取分段统计，用$last$记录上一位数字，然后枚举当前位$j$，如果$abs(j-last)>=2$，则对答案进行累加：$res+=f[i][j]$

4.敲键盘

#include <bits/stdc++.h>
using namespace std;
const int N = 12;
int a[N];       //用于储存windy数的个数
int f[N][10];   //f[i][j]表示i位数字下，最高位为j的windy数的个数

void get(){
    
    
    for(int i = 0; i <= 9; i++) f[1][i] = 1;    //预处理一位数
    for(int i = 2; i < N; i++)                  //位数枚举循环
        for(int j = 0; j <= 9; j++)             //状态：枚举第i位
            for(int k = 0; k <= 9; k++)         //枚举第i - 1位
                if(abs(k - j) >= 2) f[i][j] += f[i - 1][k];
}

int dp(int x){
    
    
    if(!x) return 0;
    int cnt = 0;
    while(x) a[++cnt] = x % 10, x /= 10; //循环取模拆位导入数组，cnt计数器记录位数
    int res = 0, last = -2;              //last表示上一位数字
    for(int i = cnt; i >= 1; i--){
    
           //从高位向低位枚举
        int now = a[i];                  //now即为当前数字
        for(int j = (i == cnt); j < now; j++)       //为了保证最高位选取范围1~ai，非最高位0~ai
            if(abs(j - last) >= 2) res += f[i][j];  //求和累加  
        if(abs(now - last) < 2) break;              //不满足windy数条件，跳出循环
        last = now;                                 //每次更新last的值
        if(i == 1) res++;                                //走到a1时需要特判
    }
    //答案小于cnt位的
    for(int i = 1; i < cnt; i++)
        for(int j = 1; j <= 9; j++) res += f[i][j];
    return res;
}

int main(){
    
    
    get();
    int l, r; cin >> l >> r;
    cout << dp(r) - dp(l - 1) << endl; 
    return 0;
}

8.插头DP

占坑，不会

9.动态DP

占坑，不会

10.概率DP

占坑，不会

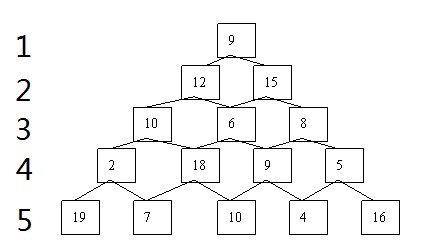
11.数塔问题

从顶部出发在每一个节点可以选择向左或者向右走，一直走到底层，要求找出一条路径，使得路径上的数字之和最大.

模板：

#include<iostream>
using namespace std;

int main()
{
    
    
    int n;
    int f[100][100] = {
    
    0};
    int dp[100][100] = {
    
    0};//状态数组
    while(cin>>n)
    {
    
    
        memset(f,0,sizeof(f));
        memset(dp,0,sizeof(dp));
        //输入数塔
        for(int i=1;i<=n;i++)
            for(int j=1;j<=i;j++)
                cin>>f[i][j];
        //边界，最底下一层的数塔dp值等于f值
        for(int j=1;j<=n;j++)
            dp[n][j] = f[n][j];
        for(int i=n-1;i>=1;i--)
        {
    
    
            for(int j=1;j<=i;j++)
            {
    
    
                //状态转移方程
                dp[i][j] = max(dp[i+1][j],dp[i+1][j+1]) + f[i][j];
            }
        }
        cout<<dp[1][1]<<endl;//dp[1][1]即为所求
    }
    return 0;
}

动态规划-优化

● 本部分例题选讲转载OI-WIKI的题解

➡侵权请联系我删除！

1.单调队列优化

单调队列优化多重背包：

有 $n$ 个物品，每个物品重量为 $w_i$ ，价值为 $v_i$ ，数量为 $k_i$ 。你有一个承重上限为 $m$ 的背包，现在要求你在不超过重量上限的情况下选取价值和尽可能大的物品放入背包。求最大价值。

转自：lys 原文链接：多重背包问题 侵删

首先回顾0-1背包的降维优化状态转移方程：

$dp[m]=max(dp[m],dp[m-v]+w,dp[m-2\ast v]+2\ast w,dp[m-3\ast v]+3\ast w,...)$

我们可以将上式 $dp[0]-->dp[m]$ 展开：

$dp[0],dp[v],dp[2\ast v],dp[3\ast v],...,dp[k\ast v]$
$dp[1],dp[v+1],dp[2\ast v+1],dp[3\ast v+1],...,dp[k\ast v+1]$
$dp[2],dp[v+2],dp[2\ast v+2],dp[3\ast v+2],...,dp[k\ast v+2]$
$...$
$dp[j],dp[v+j],dp[2\ast v+j],dp[3\ast v+j],...,dp[k\ast v+j]$

显而易见，$m$ 一定等于$ k*v + j$，其中 $0<=j<v$
所以，我们可以把 dp 数组分成 j 个类，每一类中的值，都是在同类之间转换得到的
也就是说，$dp[k\ast v+j]$ 只依赖于 $dp[j],dp[v+j],dp[2\ast v+j],dp[3\ast v+j],...,dp[k\ast v+j]$

因为我们需要的是${ dp[j], dp[v+j], dp[2v+j], dp[3v+j], … , dp[k*v+j] } $中的最大值，
可以通过维护一个单调队列来得到结果。这样的话，问题就变成了 j 个单调队列的问题

所以，我们可以得到
$dp[j]=dp[j]$
$dp[j+v]=max(dp[j]+w,dp[j+v])$
$dp[j+2v]=max(dp[j]+2w,dp[j+v]+w,dp[j+2v])$
$dp[j+3v]=max(dp[j]+3w,dp[j+v]+2w,dp[j+2v]+w,dp[j+3v])$
$...$
但是，这个队列中前面的数，每次都会增加一个 $w$ ，所以我们需要做一些转换

$dp[j]=dp[j]$
$dp[j+v]=max(dp[j],dp[j+v]-w)+w$
$dp[j+2v]=max(dp[j],dp[j+v]-w,dp[j+2v]-2w)+2w$
$dp[j+3v]=max(dp[j],dp[j+v]-w,dp[j+2v]-2w,dp[j+3v]-3w)+3w$
$...$
这样，每次入队的值是 $dp[j+k\ast v]-k\ast w$

单调队列问题，最重要的两点
1）维护队列元素的个数，如果不能继续入队，弹出队头元素

2）维护队列的单调性，即：尾值 >= dp[j + kv] - kw

本题中，队列中元素的个数应该为 s+1 个，即 0 – s 个物品 i

单调队列优化完全背包模板

#include <bits/stdc++.h>
using namespace std;
const int N = 20000 + 10;
int dp[N], pre[N], q[N];

int main()
{
    
    
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < n; ++i){
    
    
        memcpy(pre, dp, sizeof(dp));
        int v, w, s; cin >> v >> w >> s;
        for (int j = 0; j < v; ++j){
    
    
            int head = 0, tail = -1;
            for (int k = j; k <= m; k += v){
    
    
                if (head <= tail && k - s * v > q[head]) ++head;
                while (head <= tail && pre[q[tail]] - (q[tail] - j) / v * w <= pre[k] - (k - j) / v * w) --tail;
                if (head <= tail) dp[k] = max(dp[k], pre[q[head]] + (k - q[head]) / v * w);
                q[++tail] = k;
            }
        }
    }
    cout << dp[m] << endl;
    return 0;
}

例题选讲：CF372C Watching Fireworks is Fun

题目大意：城镇中有 $n$ 个位置，有 $m$ 个烟花要放。第 $i$ 个烟花放出的时间记为 $t_i$ ，放出的位置记为 $a_i$ 。如果烟花放出的时候，你处在位置 $x$ ，那么你将收获 $b_i-|a_i-x|$ 点快乐值。

设 $f_{i,j}$ 表示在放第 $i$ 个烟花时，你的位置在 $j$ 所能获得的最大快乐值。

写出 状态转移方程 ： f i , j = max ⁡ { f i − 1 , k + b i − ∣ a i − j ∣ } f_{i,j}=\max\{f_{i-1,k}+b_i-|a_i-j|\} fi,j​=max{ fi−1,k​+bi​−∣ai​−j∣}

这里的 $k$ 是有范围的， $j-(t_i-t_{i-1})\times d\le k\le j+(t_i-t_{i-1})\times d$ 。

我们尝试将状态转移方程进行变形：

由于 $\max$ 里出现了一个确定的常量 $b_i$ ，我们可以将它提到外面去。

f i , j = max ⁡ { f i − 1 , k + b i + ∣ a i − j ∣ } = max ⁡ { f i − 1 , k − ∣ a i − j ∣ } + b i f_{i,j}=\max\{f_{i-1,k}+b_i+|a_i-j|\}=\max\{f_{i-1,k}-|a_i-j|\}+b_i fi,j​=max{ fi−1,k​+bi​+∣ai​−j∣}=max{ fi−1,k​−∣ai​−j∣}+bi​

如果确定了 $i$ 和 $j$ 的值，那么 $|a_i-j|$ 的值也是确定的，也可以将这一部分提到外面去。

最后，式子变成了这个样子： f i , j = max ⁡ { f i − 1 , k − ∣ a i − j ∣ } + b i = max ⁡ { f i − 1 , k } − ∣ a i − j ∣ + b i f_{i,j}=\max\{f_{i-1,k}-|a_i-j|\}+b_i=\max\{f_{i-1,k}\}-|a_i-j|+b_i fi,j​=max{ fi−1,k​−∣ai​−j∣}+bi​=max{ fi−1,k​}−∣ai​−j∣+bi​

看到这一熟悉的形式，我们想到了什么？ 单调队列优化 。由于最终式子中的 $\max$ 只和上一状态中连续的一段的最大值有关，所以我们在计算一个新的 $i$ 的状态值时候只需将原来的 $f_{i-1}$ 构造成一个单调队列，并维护单调队列，使得其能在均摊 $O(1)$ 的时间复杂度内计算出 max ⁡ { f i − 1 , k } \max\{f_{i-1,k}\} max{ fi−1,k​} 的值，从而根据公式计算出 $f_{i,j}$ 的值。

#include <algorithm>
 #include <cstring>
#include <iostream>
using namespace std;
typedef long long ll;
const int maxn = 150000 + 10;
const int maxm = 300 + 10;

ll f[2][maxn];
ll a[maxm], b[maxm], t[maxm];
int n, m, d;

int que[maxn];

int fl = 1;
void init() {
    
    
  memset(f, 207, sizeof(f));
  memset(que, 0, sizeof(que));
  for (int i = 1; i <= n; i++) f[0][i] = 0;
  fl = 1;
}

void dp() {
    
    
  init();
  for (int i = 1; i <= m; i++) {
    
    
    int l = 1, r = 0, k = 1;
    for (int j = 1; j <= n; j++) {
    
    
      for (; k <= min(1ll * n, j + d * (t[i] - t[i - 1])); k++) {
    
    
        while (l <= r && f[fl ^ 1][que[r]] <= f[fl ^ 1][k]) r--;
        que[++r] = k;
      }

      while (l <= r && que[l] < max(1ll, j - d * (t[i] - t[i - 1]))) l++;
      f[fl][j] = f[fl ^ 1][que[l]] - abs(a[i] - j) + b[i];
    }

    fl ^= 1;
  }
}

int main() {
    
    
  cin >> n >> m >> d;
  for (int i = 1; i <= m; i++) cin >> a[i] >> b[i] >> t[i];

  // then dp
  dp();
  ll ans = -1e18;
  for (int i = 1; i <= n; i++) ans = max(ans, f[fl ^ 1][i]);
  cout << ans << endl;
  return 0;
}

2.斜率优化

占坑，待补充

3.四边形不等式优化

占坑，待补充