动态规划适合解决什么问题?
动态规划是一个很成熟的思想,很多人都对这些思想做了总结,可以用一句话概括就是:一个模型三个特征。
一个模型:即多阶段决策最优解模型,顾名思义,问题解决过程中包括多个阶段,经过每个阶段的决策可以产生该阶段对应的状态,寻找一组决策,经过这组决策可以得到希望最终得到的最优值。
三个特征:最优子结构、无后向性、重复子问题。
- 最优子结构:我们可以通过子问题的最优解推导出问题的最优解,也就是通过前一阶段的状态可以推导出后一阶段的状态。
- 无后向性:我们只关心前一阶段的状态,而不需要知道前一阶段的状态是怎么推导出来的;而且前阶段的状态一旦确定不会受后一阶段状态的影响。
- 重复子问题:不同的决策序列达到相同的某个阶段,可能会产生相同的状态。对应到使用回溯思想,当画出递归树时发现递归树中有重复的节点。
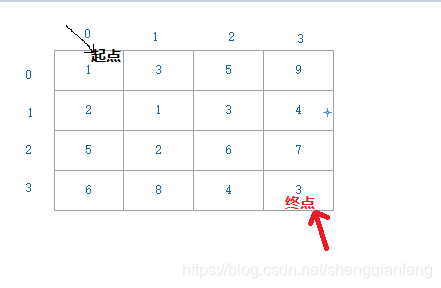
题目:如图是一个n乘以n的矩阵w[i][j],矩阵中的每个位置的空位存储的是自然数值,我们要将棋子从左上角的起始位置搬移到右下角的终点位置,每次只能向下或者向右,不能后退。从起始位置到达终点位置有很多路径可以走,我们把每条路径经过的数字加起来作为路径经过的长度。如何从(0,0)起点位置走到(n-1,n-1)终点位置,可以得到到达终点的最短路径长度?
分析:定义状态min_dist(i,j),i表示行,j表示列,min_dist(i,j)表示从(0,0)到(i,j)经过的最短路径长度。那么这个问题就是一个多阶段最优解模型,可以使用动态规划的思想去解决。
min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))
其实min_dist(i,j)就等于(i,j)存储的数值加上min_dist(i,j-1)和min_dist(i-1,j)的最小值。也就是(i,j)的上方元素和左方元素的最小值。这就是最优子结构。这个公式也是递归思想解决这个问题时用到的状态转移方程。
使用递归思想和状态转移方程求解棋盘的最短路径问题
package com.study.algorithm.recursion;
/**
* @Auther: JeffSheng
* @Date: 2019/10/17 16:20
* @Description:
* 使用递归思想和状态转移方程求解棋盘数组的最短路径问题
* 状态转移方程:
* min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))
*/
public class MinDist{
private static int[][] matrix = {{1,3,5,9}, {2,1,3,4},{5,2,6,7},{6,8,4,3}};
private static int n = 4;
private static int[][] mem = new int[4][4];
/**
* 调用 minDist(n-1, n-1);
* @param i
* @param j
* @return
*/
public static int minDist(int i, int j) {
if (i == 0 && j == 0) {
return matrix[0][0];
}
if (mem[i][j] > 0) {
return mem[i][j];
}
int minLeft = Integer.MAX_VALUE;
if (j-1 >= 0) {
minLeft = minDist(i, j-1);
}
int minUp = Integer.MAX_VALUE;
if (i-1 >= 0) {
minUp = minDist(i-1, j);
}
int currMinDist = matrix[i][j] + Math.min(minLeft, minUp);
mem[i][j] = currMinDist;
return currMinDist;
}
public static void main(String[] args) {
int min = minDist(n-1, n-1);;
System.out.println(min);
}
}
贪心、动态规划都可以用回溯解决,那么回溯是这么解决的,如下代码所示:
使用回溯思想+备忘录解决棋盘的最短路径走法问题
package com.study.algorithm.backtracking;
/**
* @Auther: JeffSheng
* @Date: 2019/10/17 14:25
* @Description:
* 使用回溯思想解决棋盘的最短路径走法问题
*/
public class MinDist {
/**
* 全局变量或者成员变量
*/
private int minDist = Integer.MAX_VALUE;
private int n = 3;
private int[][] w = {{1,3,5,9}, {2,1,3,4}, {5,2,6,7}, {6,8,4,3}};
/**
* 1 3 5 9
* 2 1 3 4
* 5 2 6 7
* 6 8 4 3
*
* 调用方式:minDistBacktracing(0, 0, 0, w, n);
* @param i 横坐标 0~3
* @param j 纵坐标 0~3
* @param dist 表示从起点(0,0)到达(i,j)之前走过的路径长度,比如起始状态(0,0)时走到(0,0)时走过的dist为1
* @param w 棋盘数组
* @param n 数组长度
* 要求:只能向右走或者向下走,不能后退
*/
public void minDistBT(int i, int j, int dist, int[][] w, int n) {
// 到达了 (n-1, n-1) 这个位置了,走过的最短路径是dist
//到达最后一个元素的位置了
if (i == n && j == n) {
if (dist < minDist) {
minDist = dist;
}
return;
}
/**
* 在(i,j)时往下走和往右走都走一遍
*/
// 往下走,更新 i=i+1, j=j
if (i < n) {
minDistBT(i + 1, j, dist + w[i][j], w, n);
}
// 往右走,更新 i=i, j=j+1
if (j < n) {
minDistBT(i, j+1, dist + w[i][j], w, n);
}
}
public static void main(String[] args) {
MinDist md = new MinDist();
md.minDistBT(0,0,0, md.w,md.n);
System.out.println(md.minDist+md.w[md.n][md.n]);
}
}
那么如何使用动态规划思想来解决这个问题呢?
思想是首先画出状态转移表,其实就是一个二维数组,每个状态在二维数组中对应的是行、列、数组值三个元素。然后根据决策先后顺序,根据递归关系,分阶段填充状态表的每个状态。最后将这个递推填表的过程翻译成代码,就是动态规划的方式了。
如图所示:
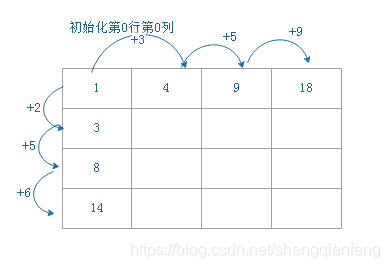
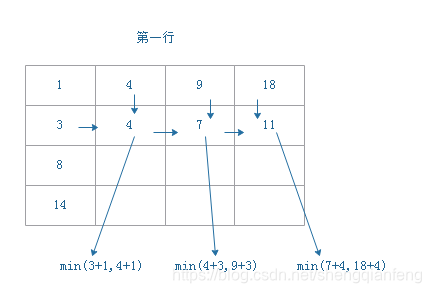
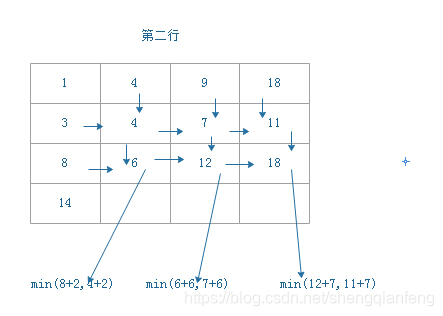
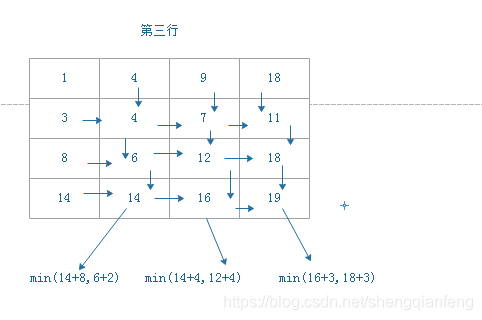
将状态转义表的填充过程翻译成代码如下:
使用动态规划思想解决棋盘的最短路径走法问题
package com.study.algorithm.dp;
/**
* @Auther: JeffSheng
* @Date: 2019/10/17 15:57
* @Description:
* 使用动态规划的思想解决棋盘的最短路径走法问题
*/
public class MinDist {
private int n = 4;
private int[][] w = {{1,3,5,9}, {2,1,3,4}, {5,2,6,7}, {6,8,4,3}};
/**
* 1 3 5 9
* 2 1 3 4
* 5 2 6 7
* 6 8 4 3
* @param matrix
* @param n
* @return
*/
public int minDistDP(int[][] matrix, int n) {
int[][] states = new int[n][n];
int sum = 0;
// 初始化 states 的第一行数据
for (int j = 0; j < n; ++j) {
sum += matrix[0][j];
states[0][j] = sum;
}
sum = 0;
// 初始化 states 的第一列数据
for (int i = 0; i < n; ++i) {
sum += matrix[i][0];
states[i][0] = sum;
}
/**
* 第一行和第一列数据填充好之后,继续依次填充其他数据
* 规则是:将待填充的数据加上左侧和上侧进行比较取最小值,得出就是(i,j)这个位置的最优解
*/
for (int i = 1; i < n; ++i) {
for (int j = 1; j < n; ++j) {
states[i][j] =
matrix[i][j] + Math.min(states[i][j-1], states[i-1][j]);
}
}
return states[n-1][n-1];
}
public static void main(String[] args) {
MinDist md = new MinDist();
int min = md.minDistDP(md.w,md.n);
System.out.println(min);
}
}