NOIP2015普及组复赛T3——求和

题目描述

一条狭长的纸带被均匀划分出了 n 个格子，格子编号从 1 到 n。每个格子上都染了一种颜色 $color_i$ （用[1，m]当中的一个整数表示），并且写了一个数字 $number_i$ 。
求和.png

定义一种特殊的三元组：(x, y, z)，其中 x，y，z 都代表纸带上格子的编号，这里的三元组要求满足以下两个条件：

$x, y, z$ 都是整数, $x < y < z, y - x = z - y$
$color_x=color_z$

满足上述条件的三元组的分数规定为 $x+z)∗(number_x+number_z)$ 。

整个纸带的分数规定为所有满足条件的三元组的分数的和。

这个分数可能会很大，你只要输出整个纸带的分数除以 $10007$ 所得的余数即可。

输入格式
第一行是用一个空格隔开的两个正整数 $n$ 和 $m$ ， $n$ 代表纸带上格子的个数， $m$ 代表纸带上颜色的种类数。

第二行有 $n$ 个用空格隔开的正整数，第 $i$ 个数字 $number_i$ 代表纸带上编号为 $i$ 的格子上面写的数字。

第三行有 $n$ 个用空格隔开的正整数，第 $i$ 个数字 $color_i$ 代表纸带上编号为 $i$ 的格子染的颜色。

输出格式
共一行，一个整数，表示所求的纸带分数除以 $10007$ 所得的余数。

数据范围
$1≤n,m≤10^5$ ,
$1≤number_i≤105$ ,
$1≤color_i≤m$

输入样例：

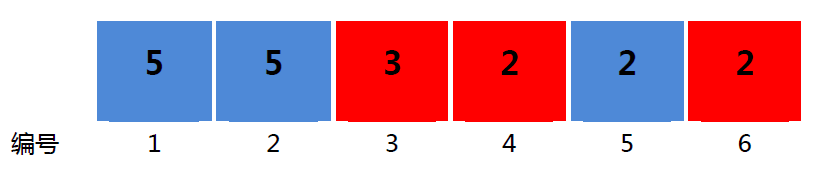
6 2
5 5 3 2 2 2
2 2 1 1 2 1

输出样例：

82

算法1

(暴力枚举) 40分 $O(n^2)$

三元组：(x, y, z)要求满足以下两个条件：

$x, y, z$ 都是整数, $x < y < z, y - x = z - y$
$color_x=color_z$

那么： $x + = 2 y$ 。由此可以枚举 $x$ 和 $y$ 的值，如果颜色相同，累加分值即可。

时间复杂度

$O(n^2)$ 。

C++ 代码

#include <iostream>
#include <cstdio>
using namespace std;

const int N = 100010, mod = 10007;

int a[N], b[N];

int main()
{
    
    
    int n, m;
    
    scanf("%d%d", &n, &m);
    
    for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);
    for(int i = 1; i <= n; i ++) scanf("%d", &b[i]);
    
    int ans = 0;
    for(int x = 1; x <= n; x ++)
    {
    
    
        for(int y = x + 1; 2 * y - x <= n; y ++)
        {
    
    
            if(b[x] == b[2 * y - x])
            {
    
    
                ans = (ans + (2 * y) % mod * (a[x] + a[2 * y - x]) % mod) % mod;
            }
        }
    }
    
    printf("%d\n", ans);
    
    return 0;
}

算法2

(数学知识、前缀和) $O (n)$

由 $z - x = 2 y$ 为偶数，可以推导出 $x, z$ 的奇偶性相同。也就是说，只要满足下列性质就可以产生得分：

$x < z$
$x$ 和 $z$ 的颜色相同
$x$ 和 $z$ 的奇偶性相同

那么可以将输入数据根据颜色和编号的奇偶性进行分组。把每个颜色分为一组、将每个颜色中再按照奇偶性分组，一共有 $m\times2$ 组。累加相同分组内的得分就是最终答案。

不妨设一个分组里有 $n$ 个格子， $x_i$ 表示格子的编号， $w_i$ 表示格子上的数字。那么这个分组的得分：

$ans = (x_1+x_2)(w_1+w_2)+(x_1+x_3)(w_1+w_3)+...+(x_1+x_n)(w_1+w_n)$
$x_2+x_3)(w_2+w_3)+(x_2+x_4)(w_2+w_4)+...+(x_2+x_n)(w_2+w_n)$
$x_3+x_4)(w_3+w_4)+...+(x_3+x_n)(w_3+w_n)$
$+ . . .$
$x_{n-1}+x_n)(w_{n-1}+w_n)$

按照格子的编号 $x_i$ 合并同类项：
$ans=x_1[(w_1+w_2)+(w_1+w_3)+(w_1+w_4)...+(w_1+w_n)]$
$x_2[(w_1+w_2)+(w_2+w_3)+(w_2+w_4)+...+(w_2+w_n)]$
$x_3[(w_1+w_3)+(w_2+w_3)+(w_3+w_4)+...+(w_3+w_n)]$
$+ . . .$
$x_n[(w_1+w_n)+(w_2+w_n)+(w_3+w_n)+...+(w_{n-1}+w_n)]$

$x_1[(n-1)w_1 + w_2+w_3+w_4+...+w_n]$
$x_2[(n-1)w_2+w_1+w_3+w_4+...+w_n]$
$x_3[(n-1)w_3+w_1+w_4+w_5+...+w_n]$
$+ . . .$
$x_n[(n-1)w_n+w_1+w_2+w_3+...+w_{n-1}]$

整理为：
$ans=x_1[(n-2)w_1+(w_1+w_2+w_3+...+w_n)]$
$x_2[(n-2)w_2+(w_1+w_2+w_3+...+w_n)]$
$x_3[(n-2)w_3+(w_1+w_2+w_3+...+w_n)]$
$+ . . .$
$x_{n}[(n-2)w_n+(w_1+w_2+...+w_n)$

即：
$ans=x_1[(n-2)w_1+\sum w_i]+x_2[(n-2)w_2+\sum w_i]+...+x_n[(n-2)w_n+\sum w_i]$

提取公因式：
$ans=(n-2)(x_1w_1+x_2w_2+...+x_nw_n)+(x_1+x_2+...+x_n)\sum w_i$

整理得：
$ans=(n-2)\sum (x_iw_i)+\sum x_i \sum w_i$

其中 $(n - 2)$ 表示该分组中格子的数量，可以通过前缀和的思想统计出来； $x_i$ 表示第 $i$ 个格子的编号； $\sum w_i$ 表示分组中前 $i$ 个格子的分数和，可同通过前缀和进行计算。

时间复杂度

$O (n)$

C++ 代码

#include <iostream>
#include <cstdio>
using namespace std;

const int N = 100010, mod = 10007;

//w[i]表示第i个格子的数字
//color[i]表示第i个格子的颜色
int w[N], color[N];
//sum[i][0]表示颜色为i、编号为偶数的格子上数字的前缀和
//cnt[i][0]表示颜色为i、编号为偶数的格子的个数
int sum[N][2], cnt[N][2];

int main()
{
    
    
    int n, m;
    
    scanf("%d%d", &n, &m);
    
    for(int i = 1; i <= n; i ++) scanf("%d", &w[i]);
    for(int i = 1; i <= n; i ++) 
    {
    
    
        scanf("%d", &color[i]);
        
        //累加分组内数字和
        sum[color[i]][i % 2] = (sum[color[i]][i % 2] + w[i]) % mod;
        //统计分组内格子个数
        cnt[color[i]][i % 2] ++;
    }
    
    int ans = 0;
    for(int i = 1; i <= n; i ++)
    {
    
    
        ans = (ans +  i * ((cnt[color[i]][i % 2] - 2) * w[i] % mod + sum[color[i]][i % 2])) % mod; 
    }
    
    printf("%d\n", ans);
    
    return 0;
}